Topological Crystals (Part 4)
Posted by John Baez
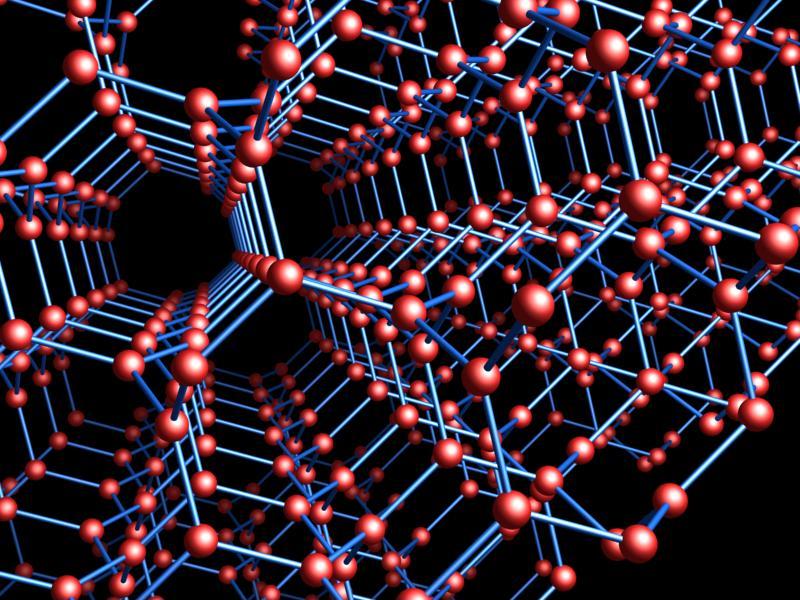
Okay, let’s look at some examples of topological crystals. These are what got me excited in the first place. We’ll get some highly symmetrical crystals, often in higher-dimensional Euclidean spaces. The ‘triamond’, above, is a 3d example.
Review
First let me remind you how it works. We start with a connected graph . This has a space of 0-chains, which are formal linear combinations of vertices, and a space of 1-chains, which are formal linear combinations of edges.
We choose a vertex in . Each path in starting at this vertex determines a 1-chain , namely the sum of its edges. These 1-chains give some points in . These points are the vertices of a graph called the maximal abelian cover of . The maximal abelian cover has an edge from to whenever the path is obtained by adding an extra edge to . We can think of this edge as a straight line segment from to .
So, we get a graph sitting inside . But this is a high-dimensional space. To get something nicer we’ll project down to a lower-dimensional space.
There’s boundary operator
sending any edge to the difference of its two endpoints. The kernel of this operator is the space of 1-cycles, . There’s an inner product on the space of 1-chains such that edges form an orthonormal basis, so we get an orthogonal projection
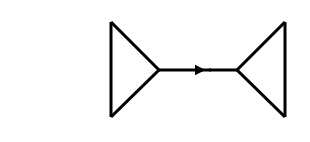
We can use this to take the maximal abelian cover and project it down to the space of 1-cycles. The hard part is checking that is one-to-one on . But that’s what I explained last time! It’s true whenever our original graph has no bridges: that is, edges whose removal would disconnect our graph, like this:
So, when is a bridgeless graph, we get a copy of the maximal abelian cover embedded in . This is our topological crystal.
Let’s do some examples.
Graphene
I showed you this one before, but it’s a good place to start. Let be this graph:

Since this graph has 3 edges, its space of 1-chains is 3-dimensional. Since this graph has 2 holes, its 1-cycles form a plane in that 3d space. If we take paths in starting at the red vertex, form the 1-chains , and project them down to this plane, we get this:
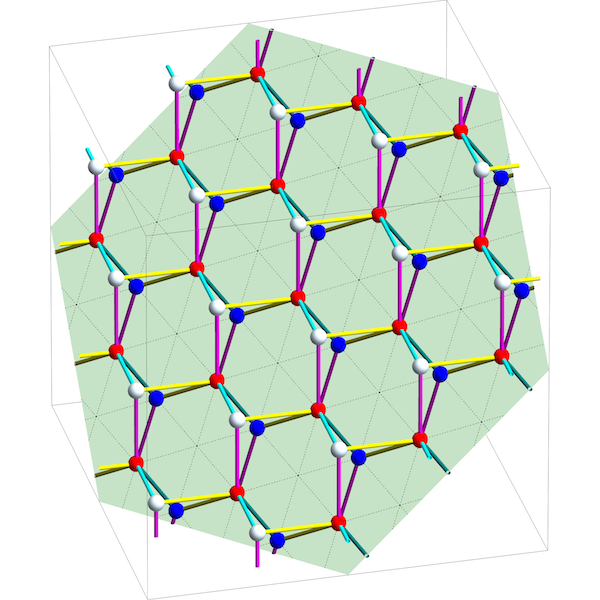
Here the 1-chains are the white and red dots. They’re the vertices of the maximal abelian cover , while the line segments between them are the edges of . Projecting these vertices and edges onto the plane of 1-cycles, we get our topological crystal:
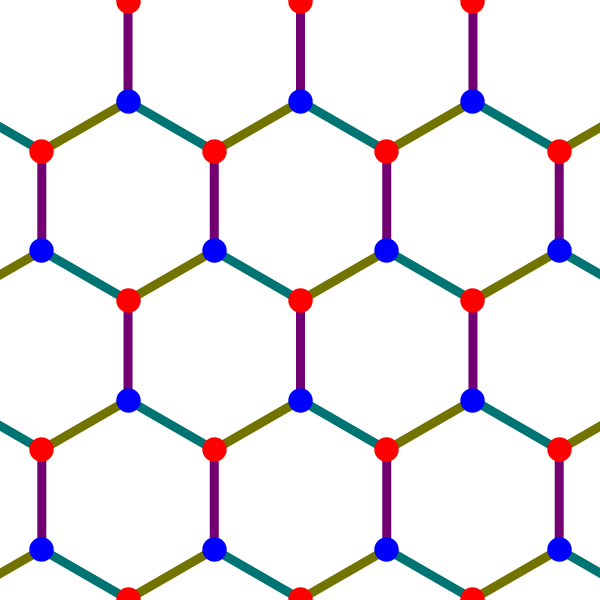
This is the pattern of graphene, a miraculous 2-dimensional form of carbon. The more familiar 3d crystal called graphite is made of parallel layers of graphene connected with some other bonds.
Puzzle 1. Classify bridgeless connected graphs with 2 holes (or more precisely, a 2-dimensional space of 1-cycles). What are the resulting 2d topological crystals?
Diamond
Now let’s try this graph:

Since it has 3 holes, it gives a 3d crystal:
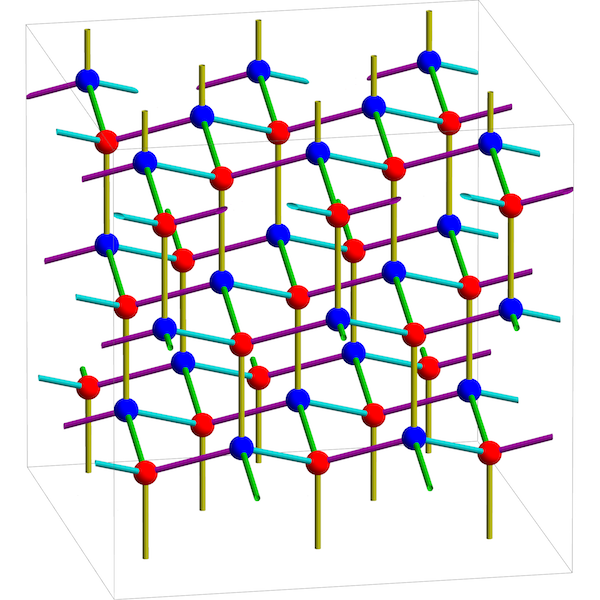
This crystal structure is famous! It’s the pattern used by a diamond. Up to translation it has two kinds of atoms, corresponding to the two vertices of the original graph.
Triamond
Now let’s try this graph:
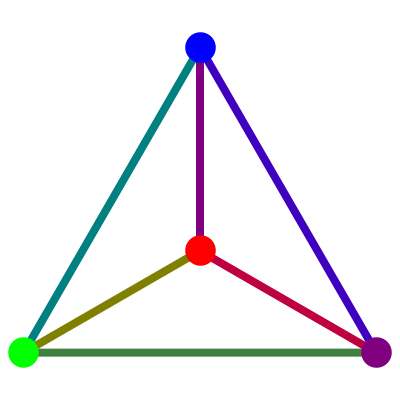
Since it has 3 holes, it gives another 3d crystal:
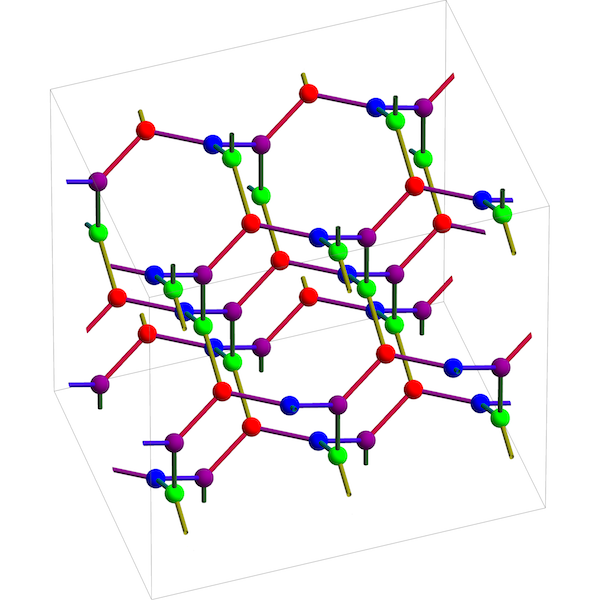
This is also famous: it’s sometimes called a ‘triamond’. If you’re a bug crawling around on this crystal, locally you experience the same topology as if you were crawling around on a wire-frame model of a tetrahedron. But you’re actually on the maximal abelian cover!
Up to translation the triamond has 4 kinds of atoms, corresponding to the 4 vertices of the tetrahedron. Each atom has 3 equally distant neighbors lying in a plane at angles from each other. These planes lie in 4 families, each parallel to one face of a regular tetrahedron. This structure was discovered by the crystallographer Laves, and it was dubbed the ‘Laves graph’ by Coxeter. Later Sunada called it the ‘ lattice’ and studied its energy minimization properties. Theoretically it seems to be a stable form of carbon. Crystals in this pattern have not yet been seen, but this pattern plays a role in the structure of certain butterfly wings.
Puzzle 2. Classify bridgeless connected graphs with 3 holes (or more precisely, a 3d space of 1-cycles). What are the resulting 3d topological crystals?
Lonsdaleite and hyperquartz
There’s a crystal form of carbon called lonsdaleite that looks like this:
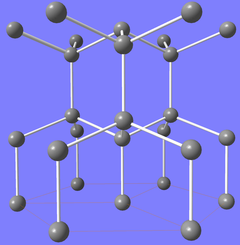
It forms in meteor impacts. It does not arise as 3-dimensional topological crystal.
Puzzle 3. Show that this graph gives a 5-dimensional topological crystal which can be projected down to give lonsdaleite in 3d space:
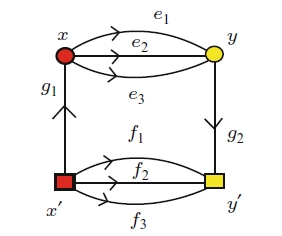
Puzzle 4. Classify bridgeless connected graphs with 4 holes (or more precisely, a 4d space of 1-cycles). What are the resulting 4d topological crystals? A crystallographer with the wonderful name of Eon calls this one hyperquartz, because it’s a 4-dimensional analogue of quartz:
All these classification problems are quite manageable if you notice there are certain ‘boring’, easily understood ways to get new bridgeless graphs with holes from old ones.
Platonic crystals
For any connected graph , there is a covering map
The vertices of come in different kinds, or ‘colors’, depending on which vertex of they map to. It’s interesting to look at the group of ‘covering symmetries’, , consisting of all symmetries of that map vertices of same color to vertices of the same color. Greg Egan and I showed that when has no bridges, also acts as symmetries of the topological crystal associated to . This group fits into a short exact sequence:
where is the group of all symmetries of . Thus, every symmetry of is covered by some symmetry of its topological crystal, while acts as translations of the crystal, in a way that preserves the color of every vertex.
For example consider the triamond, which comes from the tetrahedron. The symmetry group of the tetrahedron is this Coxeter group:
Thus, the group of covering symmetries of the triamond is an extension of by . Beware the notation here: this is not the alternating group on the 3 letters. In fact it’s the permutation group on 4 letters, namely the vertices of the tetrahedron!
We can also look at other ‘Platonic crystals’. The symmetry group of the cube and octahedron is the Coxeter group
Since the cube has 6 faces, the graph formed by its vertices and edges a 5d space of 1-cycles. The corresponding topological crystal is thus 5-dimensional, and its group of covering symmetries is an extension of by . Similarly, the octahedron gives a 7-dimensional topological crystal whose group of covering symmetries, an extension of by .
The symmetry group of the dodecahedron and icosahedron is
and these solids give crystals of dimensions 11 and 19. If you’re a bug crawling around on the the second of these, locally you experience the same topology as if you were crawling around on a wire-frame model of a icosahedron. But you’re actually in 19-dimensional space, crawling around on the maximal abelian cover!
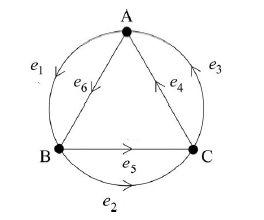
There is also an infinite family of degenerate Platonic solids called ‘hosohedra’ with two vertices, edges and faces. These faces cannot be made flat, since each face has just 2 edges, but that is not relevant to our construction: the vertices and edges still give a graph. For example, when , we have the ‘hexagonal hosohedron’:
The corresponding crystal has dimension , and its group of covering symmetries is an extension of by . The case gives the graphene crystal, while gives the diamond.
Exotic crystals
We can also get crystals from more exotic highly symmetrical graphs. For example, take the Petersen graph:
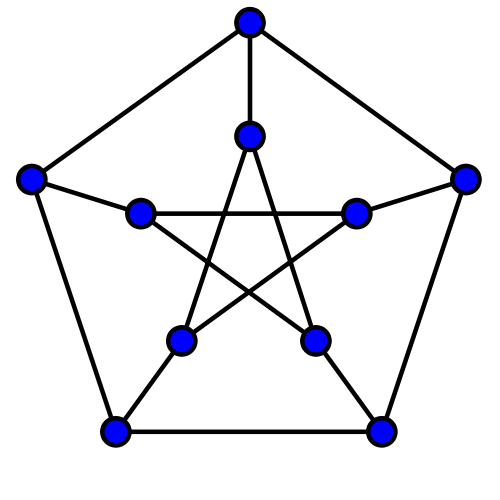
Its symmetry group is the symmetric group . It has 10 vertices and 15 edges, so its Euler characteristic is , which implies that its space of 1-cycles is 6-dimensional. It thus gives a 6-dimensional crystal whose group of covering symmetries is an extension of by .
Two more nice examples come from Klein’s quartic curve, a Riemann surface of genus three on which the 336-element group acts as isometries. These isometries preserve a tiling of Klein’s quartic curve by 56 triangles, with 7 meeting at each vertex. This picture is topologically correct, though not geometrically:

From this tiling we obtain a graph embedded in Klein’s quartic curve. This graph has edges and vertices, so it has Euler characteristic . It thus gives a 61-dimensional topological crystal whose group of covering symmetries is extension of by .
There is also a dual tiling of Klein’s curve by 24 heptagons, 3 meeting at each vertex. This gives a graph with 84 edges and 56 vertices, hence Euler characteristic . From this we obtain a 29-dimensional topological crystal whose group of covering symmetries is an extension of by .
The packing fraction
Another interesting property of a topological crystal is its ‘packing fraction’. I like to call the vertices of a topological crystal atoms, for the obvious reason. The set of atoms is periodic. It’s usually not a lattice. But it’s contained in the lattice obtained by projecting the integral 1-chains down to the space of 1-cycles:
We can ask what fraction of the points in this lattice are actually atoms. Let’s call this the packing fraction. Since acts as translations on both and , we can define it to be
For example, suppose is the graph that gives graphene:

Then the packing fraction is , as can be seen here:
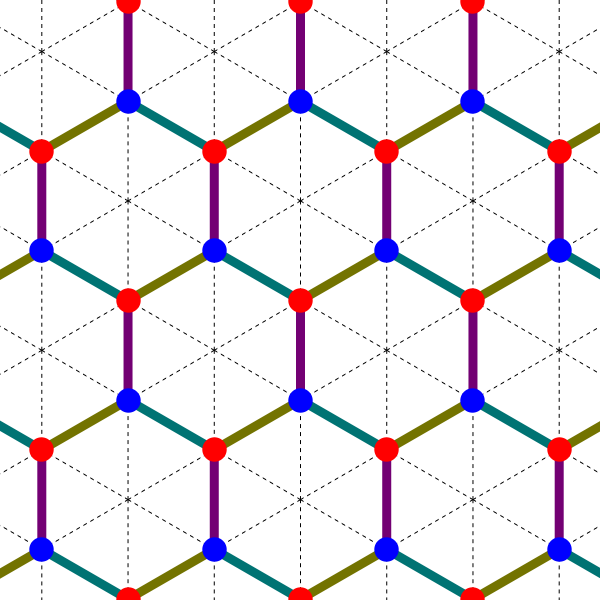
For any bridgeless connected graph , it turns out that the packing fraction is:
where is the set of vertices and is the set of spanning trees. The main tool used to prove this is Bacher, de la Harpe and Nagnibeda’s work on integral cycles and integral cuts, which in turn relies on Kirchhoff’s matrix tree theorem.
Greg Egan used Mathematica to count the spanning trees in all the examples discussed above, and this let us work out their packing fractions. They tend to be very low! For example, the maximal abelian cover of the dodecahedron gives an 11-dimensional crystal with packing fraction , while the heptagonal tiling of Klein’s quartic gives a 29-dimensional crystal with packing fraction .
So, we have some very delicate, wispy crystals in high-dimensional spaces, built from two simple ideas in topology: the maximal abelian cover of a graph, and the natural inner product on 1-chains. They have intriguing connections to tropical geometry, but they are just beginning to be understood in detail. Have fun with them!
For more, see:
- John Baez, Topological crystals.