In Praise of the Gershgorin Disc Theorem
Posted by Tom Leinster
I’m revising the notes for the introductory linear algebra class that I teach, and wondering whether I can find a way to fit in the wonderful but curiously unpromoted Gershgorin disc theorem.
The Gershgorin disc theorem is an elementary result that allows you to make very fast deductions about the locations of eigenvalues. For instance, it lets you look at the matrix
and see, with only the most trivial mental arithmetic, that the real parts of its eigenvalues must all lie between and and the imaginary parts must lie between and .
I wasn’t taught this theorem as an undergraduate, and ever since I learned it a few years ago, have wondered why not. I feel ever so slightly resentful about it. The theorem is so useful, and the proof is a pushover. Was it just me? Did you get taught the Gershgorin disc theorem as an undergraduate?
Here’s the statement:
Theorem (Gershgorin) Let be a square complex matrix. Then every eigenvalue of lies in one of the Gershgorin discs
where .
For example, if
(as above) then the three Gershgorin discs have:
- centre and radius ,
- centre and radius ,
- centre and radius .
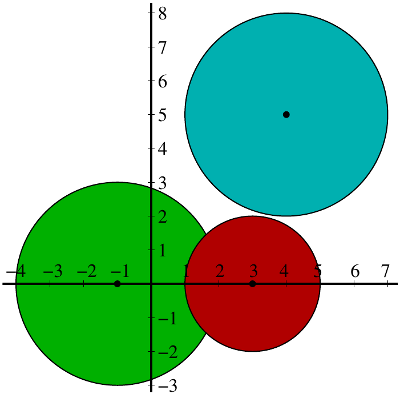
Gershgorin’s theorem says that every eigenvalue lies in the union of these three discs. My statement about real and imaginary parts follows immediately.
Even the proof is pathetically simple. Let be an eigenvalue of . Choose a -eigenvector , and choose so that is maximized. Taking the th coordinate of the equation gives
Now take the modulus of each side:
where to get the inequalities, we used the triangle inequality and then the maximal property of . Cancelling gives . And that’s it!
The theorem is often stated with a supplementary part that gives further information about the location of the eigenvalues: if the union of of the discs forms a connected-component of the union of all of them, then exactly eigenvalues lie within it. In the example shown, this tells us that there’s exactly one eigenvalue in the blue disc at the top right and exactly two eigenvalues in the union of the red and green discs. (But the theorem says nothing about where those two eigenvalues are within that union.) That’s harder to prove, so I can understand why it wouldn’t be taught in a first course.
But the main part is entirely elementary in both its statement and its proof, as well as being immediately useful. As far as that main part is concerned, I’m curious to know: when did you first meet Gershgorin’s disc theorem?




Re: In Praise of the Gershgorin Disc Theorem
Don’t think anyone’s taught me this theorem. Nice proof, though! Do you know any nice applications of it?