I’d like to tell you about a cute connection between lattices and braided monoidal categories.
And this has some fun spinoffs. For example: for any compact simple Lie group , the category of representations of any maximal torus , with its usual tensor product, has a 1-parameter family of braidings that are invariant under the action of the Weyl group.
What is this good for? I don’t know! I hope you can help me out. The best clues I have seem to be lurking here:
Braided 2-groups
Here is the kind of braided monoidal category I’m really interested in right now:
Definition. A braided 2-group is braided monoidal category such that every morphism has an inverse and every object has a ‘weak inverse’. A weak inverse of an object is an object such that
where is the unit object — that is, the unit for the tensor product.
We say two braided 2-groups and are equivalent if there’s a braided monoidal functor that’s an equivalence of categories.
In this paper, Joyal and Street showed how to classify braided 2-groups:
This paper is mainly famous for defining braided monoidal categories, but there’s a lot more in it. They published a closely related paper called ‘Braided tensor categories’ in 1992 — but it left out a lot of fun stuff, so I urge you to read this one.
Here’s the idea behind their classification. First, we take our braided 2-group and form two abelian groups:
, the group of isomorphism classes of objects of
, the group of automorphisms of the unit object
If we have an automorphism we can ‘translate’ it using the tensor product in to get an automorphism of any other object, so becomes, in a canonical way, the group of automorphisms of any object of .
Next, the associator and braiding in give two functions
How does this work? We can choose a skeleton of , a full subcategory containing one object from each isomorphism class. This will be a braided 2-group equivalent to , so from now on let’s work with this skeleton and just call it . In the skeleton, isomorphic objects are equal, so we have
and
and every object has an object with
So, the set of objects now forms an abelian group, which is just .
In this setup we can assume without loss of generality that the ‘unitor’ isomorphisms
are trivial. We still have an associator
and braiding
and these can be nontrivial, but now they are automorphisms, so we can think of them as elements of the group . So, we get maps
The data is enough to reconstruct our braided 2-group up to equivalence. To reconstruct it, we start by taking the category with one object for each element of and no morphisms except automorphisms, with the automorphism group of each object being . Then we give this category an associator using and a braiding using .
But suppose someone just hands you a choice of . Then it needs to obey some equations to give a braided 2-group! The famous pentagon identity for the associator:
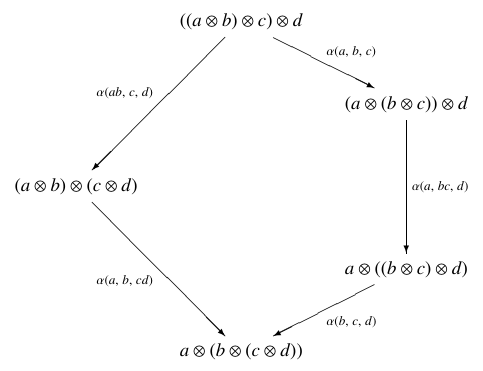
says we need
for all . Here I’m writing the operation in the group as multiplication and the operation in as addition. There are also some identities that the associator and unitor must obey, and these say:
Fans of cohomology will recognize that we’re saying is a normalized 3-cocycle on valued in . And if our 2-group weren’t ‘braided’, we’d be done: any such cocycle gives a 2-group!
But the hexagon identities for the braiding:
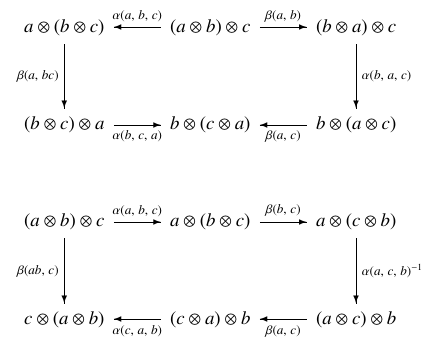
give two more equations:
Long before braided monoidal categories were invented, Eilenberg and Mac Lane called a choice of and obeying all these equations an abelian 3-cocycle on with values in . Here’s the easy, obvious part of what Joyal and Street proved:
Theorem (Joyal, Street). Any abelian 3-cocycle on with values in gives a braided 2-group with as its group of objects and as the group of automorphisms of every object. Moreover, any braided 2-group is equivalent to one of this form.
They went a lot further. For starters, they said when two 2-groups of this form are equivalent. But let’s look at some examples!
Examples
Example 1. Let’s simplify things by taking associator to be trivial: . Then all the required equations hold automatically except the hexagon identities, which become
Now I’m writing the group operation in as addition, to help you see something nice: these equations just say that is bilinear! So: any bilinear map
$$ \beta : A \times A \to BLV\theta \in \mathbb{R}L\mathbb{R}L\langle x, y \ranglex, y \in L\theta \in \mathbb{Z}L\mathbb{Z}LV\theta \in \mathbb{R}L\mathrm{U}(1)L\beta\theta\theta + 2 \pi\theta\theta = 0x,y \in L\theta0\piGT \subseteq GTV\mathfrak{t}VVLvGVVLLGL\mathrm{U}(1)GLVL^\astV^\astLL^\astGGTv \in V\exp(2 \pi v) \in TT\ell \in L^TTTRep(T)TL^[L^\ast]L^\astL^\astL^\astTL^\astV^\astL^\ast\mathrm{U}(1)\theta \in \mathbb{R}T\theta = 0\mathrm{Rep}(T)\theta0\mathrm{E}8r \in L^{\ast}r-rGV^{\ast}\theta\mathbb{Z}^n\mathbb{Z}nnn\mathrm{Rep}(T)TGG/TGG\mathrm{E}8\mathrm{A}2\mathbb{R}\mathrm{A}3\mathbb{C}\mathrm{F}_4\mathbb{H}\langle x, x \ranglexA, D,E\beta(x,x)ABAABAB\alpha\beta\beta$
But what do these equations really say? Are there any nontrivial solutions? Can we classify them?



Re: Integral Octonions (Part 12)
Re: Puzzle 2, I have been told that there are nice constructions of quantum groups (nice meaning, in particular, not just by writing down generators and relations) starting from more natural objects living in with one of its nontrivial braidings, but I don’t know where there are details written up.
Re: Puzzle 4, the significance of evenness has to do with the distinction between bilinear forms and quadratic forms: evenness means precisely that the bilinear form is induced from an integral quadratic form in the sense that . This whole story has more to do with quadratic forms than bilinear forms.
To see this we’ll pass through the homotopy hypothesis: in the same way that 2-groups are precisely pointed connected homotopy 2-types, braided 2-groups are precisely pointed connected simply connected homotopy 3-types; that is, they describe spaces whose only nontrivial homotopy groups are and . The machinery of Postnikov towers tells us that the extra data needed to describe such a space is a Postnikov invariant living in , and this is known to be precisely the group of quadratic forms .
The quadratic form is in fact a homotopy operation corresponding to the Hopf map . I believe it refines the bilinear form you wrote down, which as a homotopy operation should correspond to the Whitehead bracket , and in particular it contains strictly more information than the Whitehead bracket if has any 2-torsion. There is a nice way to visualize all of this by passing it through the cobordism hypothesis, but maybe that’s a digression.
A lattice equipped with a quadratic form gives you slightly more than a braided monoidal category: I think taking vector bundles should give you a braided monoidal category with duals and a ribbon structure, and while the braiding can only see the bilinear form the ribbon structure can see the quadratic form. Or at least that’s what Teleman says in these TFT notes.