Integral Octonions (Part 8)
Posted by John Baez
This time I’d like to summarize some work I did in the comments last time, egged on by a mysterious entity who goes by the name of ‘Metatron’.
As you probably know, there’s an archangel named Metatron who appears in apocryphal Old Testament texts such as the Second Book of Enoch. These texts rank Metatron second only to YHWH himself. I don’t think the Metatron posting comments here is the same guy. However, it’s a good name for someone interested in lattices and geometry, since there’s a variant of the Cabbalistic Tree of Life called Metatron’s Cube, which looks like this:
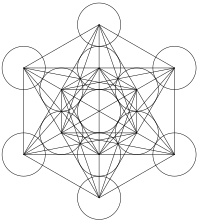
This design includes within it the root system, a 2d projection of a stellated octahedron, and a perspective drawing of a hypercube.
Anyway, there are lattices in 26 and 27 dimensions that play rather tantalizing and mysterious roles in bosonic string theory. Metatron challenged me to find octonionic descriptions of them. I tried.
Given a lattice in -dimensional Euclidean space, there’s a way to build a lattice in -dimensional Minkowski spacetime. This is called the ‘over-extended’ version of .
If we start with the lattice in 8 dimensions, this process gives a lattice called , which plays an interesting but mysterious role in superstring theory. This shouldn’t come as a complete shock, since superstring theory lives in 10 dimensions, and it can be nicely formulated using octonions, as can the lattice .
If we start with the lattice called , this over-extension process gives a lattice . This describes the ‘cosmological billiards’ for the 3d compactification of the theory of gravity arising from bosonic string theory. Again, this shouldn’t come as a complete shock, since bosonic string theory lives in 26 dimensions.
Last time I gave a nice description of : it consists of self-adjoint matrices with integral octonions as entries.
It would be nice to get a similar octonionic description of . But it’s actually easier to go up to 27 dimensions, because the space of self-adjoint matrices with octonion entries is 27-dimensional. And indeed, there’s a 27-dimensional lattice waiting to be described with octonions.
You see, for any lattice in -dimensional Euclidean space, there’s also a way to build a lattice in -dimensional Minkowski spacetime, called the ‘very extended’ version of .
If we do this to we get an 11-dimensional lattice called , which has mysterious connections to M-theory. But if we do it to we get a 27-dimensional lattice sometimes called . You can read about both these lattices here:
- Peter C. West, E11 and M theory.
I’ll prove that has a nice description in terms of integral octonions. I’ll almost do something similar for , but in fact I’ll succeed for a lattice containing it, which is twice as dense.
To do these things, I’ll use the explanation of over-extended and very extended lattices given here:
- Matthias R. Gaberdiel, David I. Olive and Peter C. West, A class of Lorentzian Kac–Moody algebras.
These constructions use a 2-dimensional lattice called . Let’s get to know this lattice. It’s very simple.
A 2-dimensional Lorentzian lattice
Up to isometry, there’s a unique even unimodular lattice in Minkowski spacetime whenever its dimension is 2 more than a multiple of 8. The simplest of these is : it’s the unique even unimodular lattice in 2-dimensional Minkowski spacetime.
There are various ways to coordinatize . The easiest, I think, is to start with and give it the metric with
when . Then, sitting in , the lattice is even and unimodular. So, it’s a copy of .
Let’s get to know it a bit. The coordinates and are called lightcone coordinates, since the and axes form the lightcone in 2d Minkowski spacetime. In other words, the vectors
are lightlike, meaning
Their sum is a timelike vector
since the inner product of with itself is negative; in fact
Their difference is a spacelike vector
since the inner product of with itself is positive; in fact
Since the vectors and are orthogonal and have length in the metric , we get a square of area with corners
that is,
If you draw a picture, you can see by dissection that this square has twice the area of the unit cell
So, the unit cell has area 1, and the lattice is unimodular as claimed. Furthermore, every vector in the lattice has even inner product with itself, so this lattice is even.
Over-extended lattices
Given a lattice in Euclidean ,
is a lattice in -dimensional Minkowski spacetime, also known as . This lattice is called the over-extension of .
A direct sum of even lattices is even. A direct sum of unimodular lattices is unimodular. Thus if is even and unimodular, so is .
All this is obvious. But here are some deeper facts about even unimodular lattices. First, they only exist in when is a multiple of 8. Second, they only exist in when is a multiple of 8.
But here’s the really amazing thing. In the Euclidean case there can be lots of different even unimodular lattices in a given dimension. In 8 dimensions there’s just one, up to isometry, called . In 16 dimensions there are two. In 24 dimensions there are 24. In 32 dimensions there are at least 1,160,000,000, and the number continues to explode after that. On the other hand, in the Lorentzian case there’s just one even unimodular lattice in a given dimension, if there are any at all.
More precisely: given two even unimodular lattices in , they are always isomorphic to each other via an isometry: a linear transformation that preserves the metric. We then call them isometric.
Let’s look at some examples. Up to isometry, is the only even unimodular lattice in 8-dimensional Euclidean space. We can identify it with the lattice of integral octonions, , with the inner product
is usually called . Up to isometry, this is the unique even unimodular lattice in 10 dimensions. There are lots of ways to describe it, but last time we saw that it’s the lattice of self-adjoint matrices with integral octonions as entries:
where the metric comes from times the determinant:
We’ll see a fancier formula like this later on.
There are 24 even unimodular lattices in 24-dimensional Euclidean space. One of them is
Another is the lattice of vectors in where the components are either all integers or all half-integers and their sum is even. This contains the lattice that I mentioned earlier. It’s twice as dense. I’ll explain it later.
If we take the over-extension of any of these even unimodular lattices in 24-dimensional Euclidean space, we get an even unimodular lattice in 26-dimensional Minkowski spacetime… and all these are isometric! The over-extension process ‘washes out the difference’ between them. In particular,
This is nice because up to a scale factor, is the lattice of integral octonions. So, there’s a description of using three integral octonions! But the story is prettier if we go up an extra dimension.
Very extended lattices
After the over-extended version of a lattice in Euclidean space comes the ‘very extended’ version, called . If you ponder the paper by Gaberdiel et al, you can see this is the direct sum of the over-extension and a 1-dimensional lattice called . is just with the metric
It’s even but not unimodular.
In short, the very extended version of is
If is even, so is . But if is unimodular, this will not be true of .
The very extended version of is called . The very extended version of is called . This a fascinating thing, and it would be nice to describe it using octonions. But it will be easier to work with a lattice that’s twice as dense: the very extended version of .
Now it’s time to explain this ‘twice as dense’ business.
Doubling the density of Dn
The lattice is very simple. Take an -dimensional checkerboard with alternating red and black hypercubes. Put a dot in the middle of each black hypercube. That’s the lattice!
More precisely, the lattice consists of all -tuples of integers that sum to an even integer. Requiring that they sum to an even integer picks out the center of every other hypercube in our checkerboard.
Here’s a basis of vectors for the lattice:
The same pattern works in any dimension: the first vector has two s followed by a bunch of zeros, but the rest of the vectors are all just shifted versions of the second. I’ve chosen them to be simple roots for , but that’s not so important now.
What really matters is this. The dot product of any basis vector with itself is even, and the dot product of any two different ones is an integer. Thus, the lattice they generate, the lattice, is even: the dot product of any vector with itself is even.
Also, the determinant of the matrix formed by our basis vectors:
is 2. In any dimension, this sort of determinant gives . So, the volume of the unit cell in lattice is always 2. So, it’s not unimodular.
To get something unimodular, we can double the density by taking the union of and a copy of translated by the vector
Let’s call this union . A lot of people call it , but we’re using plus signs for too many other things already. I’m calling it because it’s doubly dense, and also because it’s the union of two shifted copies of .
is the way carbon atoms are arranged in a diamond!

This pattern is called the diamond cubic. It’s beautiful, but it’s not a lattice in the mathematical sense. is a lattice only when is even. Here’s the story:
- In any dimension, the volume of the Voronoi cells of is 1, so we can say it’s unimodular.
- In even dimensions, and only those, is lattice. After all, only then does the sum of with itself again lie in .
- In dimensions that are multiples of 4, and only those, is an integral lattice, meaning that the dot product of any two vectors in the lattice is an integer. After all, only then is the inner product of with itself an integer.
- In dimensions that are multiples of 8, and only those, is an even lattice, meaning that the dot product of any vector with itself is even. After all, only then is the inner product of even.
As I mentioned before, even unimodular lattices are possible in Euclidean space only when the dimension is a multiple of 8. is none other than our friend ! But what we really need now is , since it’s an even unimodular lattice in 24 dimensions. I’d like to have a nice octonionic description of
but I’ll actually get one for
which is twice as dense. We could use this to get an octonionc description of , but I won’t do that.
Lattices in the exceptional Jordan algebra
Now we are ready to have some fun!
Let be the space of self-adjoint octonionic matrices. It’s 27-dimensional since a typical element looks like
where . It’s called the exceptional Jordan algebra. We don’t need to know about Jordan algebras now, but this concept encapsulates the fact that if , so is .
There’s a 2-parameter family of metrics on the exceptional Jordan algebra that are invariant under all Jordan algebra automorphisms. They have
for with . Some are Euclidean and some are Lorentzian.
Sitting inside the exceptional Jordan algebra is the lattice of self-adjoint matrices with integral octonions as entries:
And here’s the cool part:
Theorem. There is a Lorentzian inner product on the exceptional Jordan algebra that is invariant under all automorphisms and makes the lattice isometric to .
Proof. We will prove that the metric
obeys all the conditions of this theorem. From what I’ve already said, it is invariant under all Jordan algebra automorphisms. The challenge is to show that it makes isometric to . But instead of , we can work with , since we have seen that
Let us examine the metric in more detail. Take any element :
where . Then
while
Thus
It follows that with this metric, the diagonal matrices are orthogonal to the off-diagonal matrices. An off-diagonal matrix is a triple , and has
Thanks to the factor of 2, this metric makes the lattice of these off-diagonal matrices isometric to . Since
it thus suffices to show that the 3-dimensional Lorentzian lattice of diagonal matrices in is isometric to
A diagonal matrix is a triple , and on these triples the inner product is given by
If we restrict attention to triples of the form , we get a 2-dimensional Lorentzian lattice: a copy of with inner product
This is just .
We can use this to show that the lattice of all triples , with the inner product , is isometric to .
Remember, is a 1-dimensional lattice generated by a spacelike vector whose norm squared is 2. So, it suffices to show that the lattice is generated by vectors of the form together with a spacelike vector of norm squared 2 that is orthogonal to all those of the form .
To do this, we need to describe the inner product on more explicitly. For this, we can use polarization identity
Remember, if we have
So, if we also have , the polarization identity gives
We are looking for a spacelike vector that is orthogonal to all those of the form . For this, it is necessary and sufficient to have
and
An example is . This has
so it is spacelike, as desired. Even better, it has norm squared two. And even better, this vector , along with those of the form , generates the lattice .
So we have shown what we needed: the lattice of all triples is generated by those of the form together with a spacelike vector with norm squared 2 that is orthogonal to all those of the form .
This theorem has three nice spinoffs:
Corollary 1. With the same Lorentzian inner product on the exceptional Jordan algebra, the lattice is isometric to the sublattice of where a fixed diagonal entry is set equal to zero, e.g.:
Proof. Use the fact that with the metric , the diagonal matrices
form a copy of , so the matrices above form a copy of
Corollary 2. With the same Lorentzian inner product on the exceptional Jordan algebra, the lattice is isometric to the sublattice of where two fixed off-diagonal entries are set equal to zero, e.g.:
Proof. Use the fact that with the metric , the diagonal matrices
form a copy of , so the matrices above form a copy of
Corollary 3. With the same Lorentzian inner product on the exceptional Jordan algebra, the lattice is isometric to the sublattice of where two fixed off-diagonal entries and one diagonal entry are set equal to zero, e.g.:
Proof. Use the previous corollary; this is the obvious copy of inside .

Re: Integral Octonions (Part 8)
This is very nice!
I’ve been pondering that metric:
and wondering if there’s some setting where things work as nicely in the case as they do for the . I think this metric is Lorentzian for any on the self-adjoint matrices over any division algebra , with the identity matrix as a timelike vector, while all self-adjoint pairs of off-diagonal matrix elements are spacelike, as well as the diagonal matrices such as .
You say that for this metric is invariant under the Jordan algebra automorphisms. But do you know if there’s some kind of systematic representation of on the matrices (where )?