Integral Octonions (Part 6)
Posted by John Baez
You can add and subtract integers. You can multiply them. You can also think about them geometrically, as a lattice in the real line.
The same is true for the Gaussian integers in the complex plane:
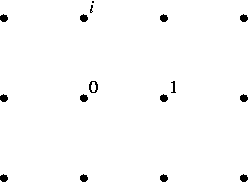
or, for that matter, the Eisenstein integers:
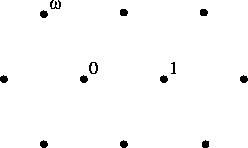
Things get even more interesting for the quaternions and octonions. There are various different concepts of ‘integer’ for these number systems, but I’m especially interested in the so-called ‘Cayley integral octonions’, because they’re the most exotic and mysterious of the lot.
When it comes to their additive and geometrical aspects, the Cayley integers look just like the lattice in an 8-dimensional Euclidean vector space, rescaled so that the shortest nonzero vectors have length 1. In Parts 3, 4 and 5 of this series we studied these aspects in loving detail. You can now see all the previous parts in one place here.
Now I’d like to finally get around to discussing the multiplicative structure of the Cayley integers.
First, let’s remember how to multiply octonions!
The octonions are an 8-dimensional real vector space with a basis given by 1 and seven square roots of -1 called . Multiplying anything by 1 does the obvious thing. Squaring a square root of -1 does the obvious thing. So all we need to know is how to multiply two different guys and . And for this, you can just draw a little chart:
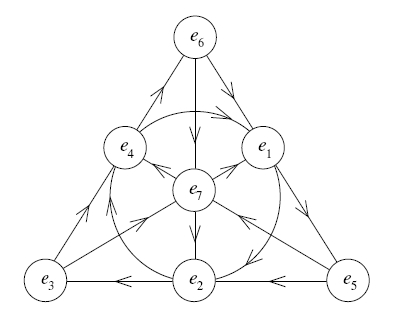
This is a picture of the Fano plane, a projective plane with 7 points and 7 lines, where we count the circle containing as an honorary ‘line’. Each line contains 3 points, and each of these triples is equipped with a cyclic order as indicated by the arrows. The rule is that if are cyclically ordered in this way, we define
So, for example, times is , but times is .
If you think it’s hard to remember this chart, you’re wrong!
First of all, it doesn’t matter what names we give to the 7 points. We could name them after the 7 dwarves in the Disney version of Snow White if we wanted — though we’d probably get sued for copyright infringement. The only reason this particular numbering scheme is nice is that with this scheme we get
where we work mod 7, and
where doubling the indices mod 7 rotates the picture a third of a turn. But these cute facts only come in handy if you spend a lot of time multiplying octonions. Since I try to work at a higher level of abstraction whenever possible, I rarely need them.
Second of all, it doesn’t matter whether all your little arrows go counterclockwise or clockwise, as long as your consistent.
Third of all, it doesn’t whether your little arrows point from the corners of the equilateral triangle to the midpoints of the opposite sides, or vice versa.
Puzzle 1. Prove that if we reverse the arrows on the lines connecting the corners of the equilateral triangle to the midpoints of the opposite sides, we get a new multiplication that is isomorphic to the old one.
So, there’s not as much arbitrary baloney to remember as you might think! Anyone can remember how to multiply octonions, and I’m surprised they’re not taught in elementary school right after category theory.
Various lattices in the octonions present themselves as possible octonionic analogues of the integers, but the best candidate is the least obvious. Let’s run through them all, following the book by Conway and Smith.
Starting with the most obvious, the Gravesian integers are octonions of the form
where all the coefficients are integers. The Kleinian integers are octonions where the are either all integers or all half-integers. Both these are lattices closed under multiplication, but they’re not the densest possible lattices with this property.
To get a denser lattice, first pick a line in the chart above. Then, take all integral linear combinations of
- Gravesian integers,
- octonions of the form where , and lie on this line, and
- octonions of the form where all lie off this line.
Conway and Smith call the resulting lattice the double Hurwitzian integers. Actually we get 7 isomorphic copies of the double Hurwitzian integers this way, one for each line. It’s easy to see that any one of these — hence all of them — are closed under multiplication.
But we can do better! We can get even denser lattices that are closed under multiplication!
One obvious guess is to take the union of all 7 copies of the double Hurwitzian integers. This gives a collection of octonions called the Kirmse integers. It’s a copy of our beloved lattice: the densest possible lattice packing of balls in 8 dimension, where each ball touches 240 others!
Be careful: in earlier posts, we used at a version of the lattice where the shortest vectors had length . Now it’s been rescaled so they’re unit vectors. It’s also been rotated in some sneaky way. But apart from that, it’s still our friend .
To see a hint of why this is true, let’s count the lattice vectors of norm one:
- First, we have for . There are vectors of this form.
- Second, we have where , and all lie on some line in the Fano plane. There are of these.
- Third, we have where all lie off some line. There are of these.
So, we indeed get a total of .
However, there’s some bad news:
Puzzle 2. Show the Kirmse integers are not closed under multiplication!
Curiously, I had just been thinking about this back in 2003 when I got Conway and Smith’s book in my mail. After checking a couple of cases, I’d jumped to the conclusion that this set of octonions is closed under multiplication. I was shocked to read that it is not. But I was comforted to hear that I was not the first to make this mistake! According to Coxeter, a fellow named Johannes Kirmse published this erroneous claim, and the term ‘Kirmse integers’ is just a way of needling this poor guy for the rest of time.
To fix Kirmse’s mistake, we need to perform a curious trick. Pick a number from 1 to 7. Then, take all the Kirmse integers
and switch the coefficients and . The resulting lattice is just a reflected version of the Kirmse integers, so it’s still a copy of . But bizarrely, it’s now closed under multiplication!
We call this lattice the Cayley integers. But since this trick involved an arbitrary choice, there are 7 different copies of the Cayley integers containing the Gravesian integers. And this is as good as it gets: each one is maximal among lattices closed under multiplication!
Using the Cayley integers, we can define ‘integral forms’ of many algebraic gadgets related to the octonions. We get a lot of interesting stuff. Some of it is related to the Leech lattice! So, I hope that someday we’ll get a good connection between the octonions and monstrous moonshine.
There’s a lot more to say, but I think I’ll stop here, with a big puzzle I don’t know the answer to:
Puzzle 3. Find a deeper explanation of the Cayley integers, perhaps by avoiding the arbitrary choice, or describing an interesting algebraic structure that involves all 7 choices.
Also, a few smaller puzzles:
Puzzle 4. Let where be the seven different kinds of Cayley integers. Show that the intersection is precisely the set of Kleinian integers.
Puzzle 5. Let be the set of all products where and . Show that if , then for all .
Puzzle 6. Show that if , the set is not a lattice.

Re: Integral Octonions (Part 6)
Do you know if there’s any connection between multiplication of the Cayley integers and the multiplication imposed on by identifying it with the icosian ring?