M13
Posted by John Baez
People of a certain ilk wonder why we need groupoids. Why aren’t groups enough?
There are many answers to this question. The answers provided by Alan Weinstein and Ronald Brown should be convincing to any open-minded topologist or geometer. But what if you’re a group theorist… say, someone who studies finite groups? What do groupoids have to offer you?
I just noticed a nice answer to this question. The Mathieu group is somewhat easier to understand if you think of it as part of a groupoid. John Conway calls this groupoid .
Don’t confuse this with the Hercules Cluster, which is called M13:

The font makes a big difference! The globular cluster M13 is a Messier object. The groupoid is a less messy object.
I’ve been looking for a good excuse for that pun for years. I could stop here and be completely satisfied! But now that I’ve got your curiosity up, let me describe and .
Finite simple groups come in a bunch of infinite families, but there are also 26 exceptional ones, the sporadic finite simple groups. The first of these to be discovered were the Mathieu groups, and the second smallest of these is . The smallest is , but this is conveniently described as the subgroup of that fixes a chosen point. So, anyone seriously interested in finite groups should get to know .
Until recently I just knew three descriptions of .
The easiest comes from Conway and Sloane’s classic book Sphere Packings, Lattices and Groups. If you get 12 equal-sized balls to touch a central one of the same size, and arrange them to lie at the corners of a regular icosahedron, they don’t touch their neighbors:
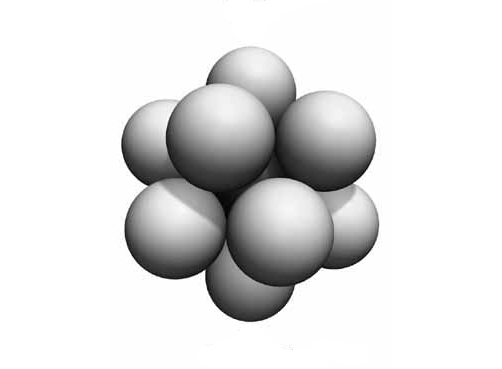
There’s even room to roll them around in interesting ways! For example, you can twist 5 of them around clockwise so that this arrangement:
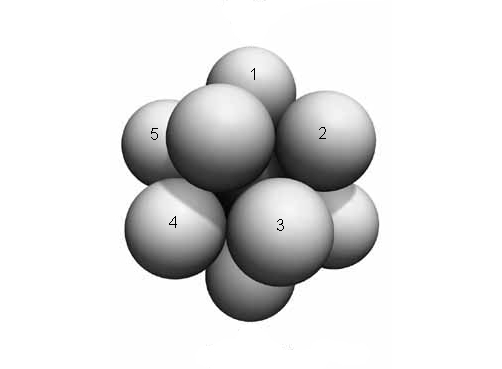
becomes this:
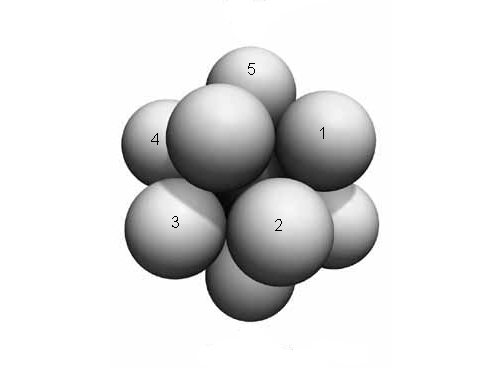
We can generate lots of permutations of the 12 outer balls using twists of this sort - in fact, all even permutations. But suppose we only use moves where we first twist 5 balls around clockwise and then twist 5 others counterclockwise. These generate a smaller group: the Mathieu group !
Here’s a second description of , which is very terse but much less concrete. Let’s say a group of permutations of some set is -tuply transitive if given any ordered -tuple of distinct elements of that set, and any other -tuple of this sort, there’s a permutation in the group that carries one to the other. It turns out that aside from the symmetric groups , which consist of all permutations of an -element set, and the alternating groups , which consist of all the even permutations, there are only four finite permutation groups that are -tuply transitive for . Moreover, they’re all Mathieu groups!
This lets us characterize in a very speedy way. Up to isomorphism, it’s the only quintuply transitive group of permutations of a 12-element set other than and .
In terms of our ‘rolling ball’ description of , this means that given any list of 5 balls, and any other list of 5 balls, there exists an element of mapping the first list to the second. In fact there’s a unique element of that does the job, so we say this group of permutation is sharply quintuply transitive.
Unlike the first description, the second one doesn’t really let us get our hands on . But given that it’s sharply quintuply transitive, it’s at least easy to count the elements of . There must be one for each way to pick a list of 5 distinct things out of 12. So, this group has
elements.
The third description goes is more concrete than the second. Up to isomorphism, there’s a unique way to choose a bunch of 6-element subsets of a 12-element set, called blocks, such that each 5-element subset lies in a unique block. Given this, consists of all permutations of the 12-element set that map blocks to blocks.
Of course, to get your hands on using this description, you need to know how to find 6-element blocks so that each 5-element subset lies in a unique block. If you were stuck on a desert island you could eventually figure it out. But since you’re not, I’ll tell you.
Take a 12-point set and think of it as the projective line over : in other words, the integers mod 11 together with a point called . Among the integers mod 11, six are perfect squares:
Let this set be a block. From this, we get all the other blocks by applying fractional linear transformations:
where the matrix
has determinant 1. If the fractional linear transformation involves dividing by zero, we say it gives .
This description is nice because it connects to lots of good math. In fact, I’m no longer sure the description using the groupoid is better! But let me give it anyway—because even if it isn’t ‘better’, it’s still very pretty.
Start with the projective plane over . This is the set of lines through the origin in a 3d vector space over , but Bob Harris has drawn a nice picture of it:
Any two points lie on a unique line, and any two lines intersect in a unique point. Each line contains 4 points and each point lies on 4 lines. There are 13 points and 13 lines.
Now, put a ‘counter’ on each point except one. A move consists of moving a counter from any point to the empty point , then exchanging the two other counters on the line containing and .
consists of the permutations of counters that can be obtained by composing finite sequence of moves. This is not a group, since we can only compose two moves if the point left empty after carrying out the first move is the empty point at the start of the second move. But it’s a groupoid!
More precisely: the objects of are the 13 positions of the point that’s left empty. The morphisms are the permutations of counters that arise from finite sequences of composable moves.
can then be defined as the subgroupoid consisting of morphisms that leave a particular point empty. This is actually a group!
This should remind you of the famous 15-puzzle, which also gives a groupoid:
But the groupoid seems to be more important, mathematically speaking. You can read more about it here:
-
John H. Conway, Noam D. Elkies and Jeremy L. Martin, The Mathieu group and its pseudogroup extension , Experimental Mathematics 15 (2006), 223–236.
- Mathieu groupoid, Wikipedia.
People of a certain ilk—the sort who challenge us to prove our interests are interesting—will ask how helps us prove new theorems about . I don’t know the answer to that question. Do you?
Another obvious question is whether a similar puzzle exists for , a much deeper group, which can be defined as the unique quintuply transitive group of permutations of 24 things. So far I’ve only seen a lonely MathOverflow question about this, with no answer.
Notice that if we think of groups as one-object groupoids, is equivalent, as a groupoid, to . So, arguably, this is a case where an important finite group is equivalent to a finite groupoid that’s easier to describe. So we should look for more. It would be nice if other sporadic finite simple groups were best understood using groupoids in this way, but I don’t have much evidence for that yet. Just .
And finally… here’s one more thing about , which I should mention before I forget.
Take a deck of 24 cards. Cut it exactly in half, so you’ve got 12 in each hand. Shuffle them perfectly, so the cards alternate. There are two ways to do this: the card that was originally on top can stay on top, or not. Keep doing this as often as you want. You get lots of permutations of the cards this way. How many? This many:
And here’s the really cool part: they form a group that contains ! It’s the semidirect product of and . I recently learned this here:
- Persi Diaconis, Ronald Graham and William M. Kantor, The mathematics of perfect shuffles, Advances in Applied Mathematics 4 (1983), 175–196.
I thank Graham Jones for pointing me in this direction, which eventually led me to read about .
Here’s a hint about why we get the semidirect product of and . The shuffles I’m talking about, called perfect shuffles, give permutations with a special property: they commute with turning the deck upside down! So, we can take our deck of cards and divide it into 12 pairs—the top card and the bottom card, the card second from the top and the card second from the bottom, and so on—and our shuffles will send each such pair to another pair.
So, we get permutations of these 12 pairs of the cards in our deck, and the group of permutations we get is . But we also get various ways of permuting the two cards within each pair… and these permutations form the group .
Why not ? Well, think about it… or read the paper!





Re: M13
isn’t the smallest sporadic group—that’s .
If you take the action of on points, then the subgroup which fixes one point is , which is also simple.
(In fact, has two different actions on objects, related by an outer automorphism of in a manner analogous to the two actions of on objects. Indeed, in some ways, is like a sort of hyped-up . As you mentioned, sends the -point “blocks” to blocks in the action on points. (The complement of a block is also a block.) The subgroup of which sends a block to itself is (this follows immediately from the fact that is -transitive). This subgroup acts as all permutations on each of the complementary blocks, but via two different actions, related by an outer automorphism of . fits into in the same way, but the process stops there: has only trivial outer automorphism group.)