The Free Modular Lattice on 3 Generators
Posted by John Baez
The set of subspaces of a vector space, or submodules of some module of a ring, is a lattice. It’s typically not a distributive lattice. But it’s always modular, meaning that the distributive law
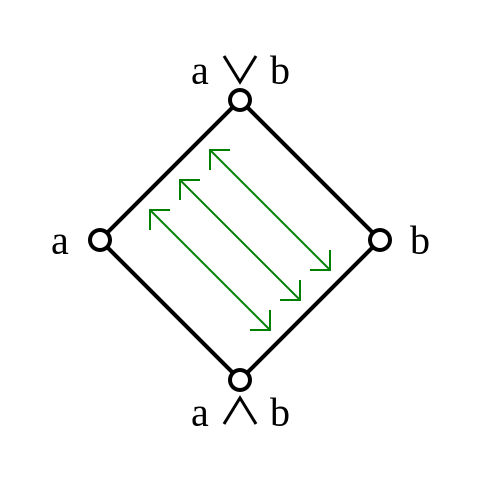
holds when or . Another way to say it is that a lattice is modular iff whenever you’ve got , then the existence of an element with
is enough to imply . Yet another way to say it is that there’s an order-preserving map from the interval to the interval that sends any element to , with an order-preserving inverse that sends to :
Dedekind studied modular lattices near the end of the nineteenth century, and in 1900 he published a paper showing that the free modular lattice on 3 generators has 28 elements.
One reason this is interesting is that the free modular lattice on 4 or more generators is infinite. But the other interesting thing is that the free modular lattice on 3 generators has intimate relations with 8-dimensional space. I have some questions about this stuff.
One thing Dedekind did is concretely exhibit the free modular lattice on 3 generators as a sublattice of the lattice of subspaces of . If we pick a basis of this vector space and call it , he looked at the subspaces
By repeatedly taking intersections and unions, he built 28 subspaces starting from these three.
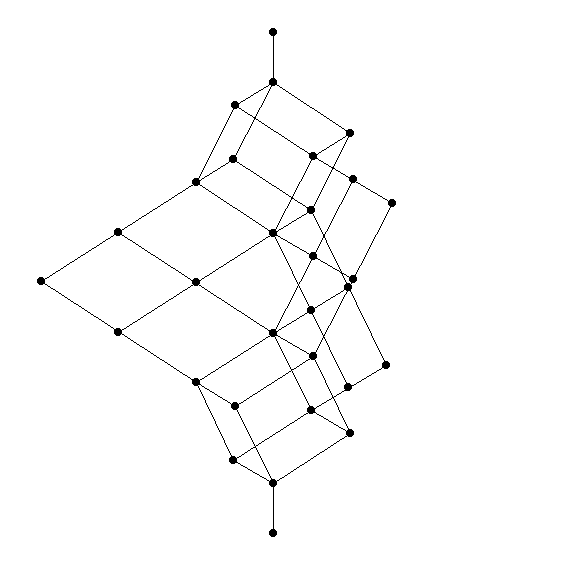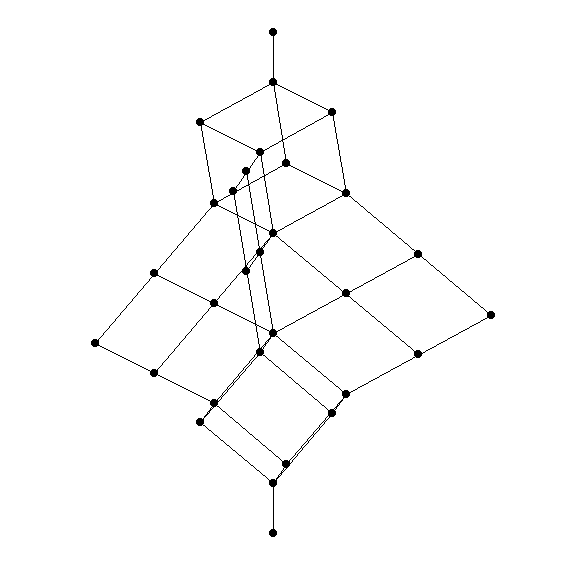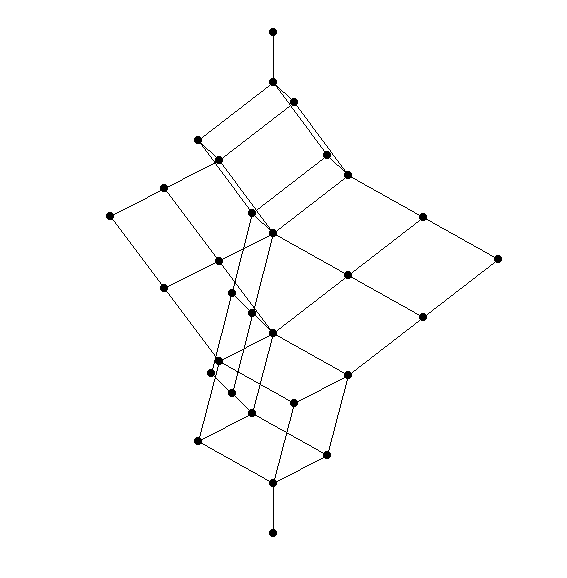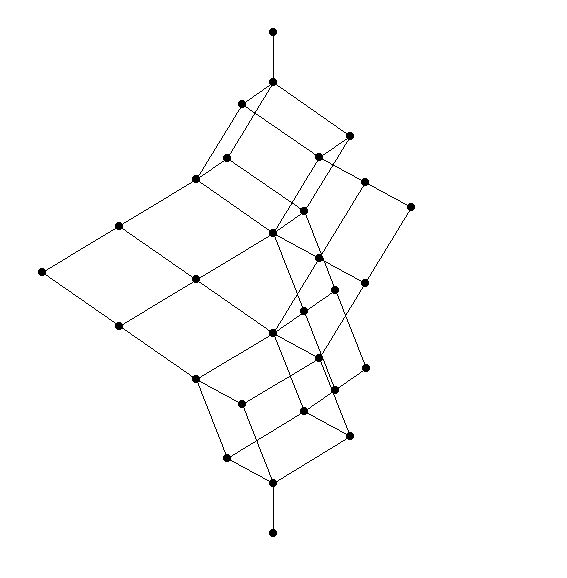
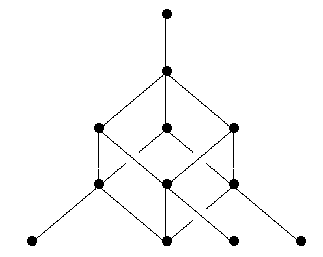
This proves the free modular lattice on 3 generators has at least 28 elements. In fact it has exactly 28 elements. I think Dedekind showed this by working out the free modular lattice ‘by hand’ and noting that it, too, has 28 elements. It looks like this:
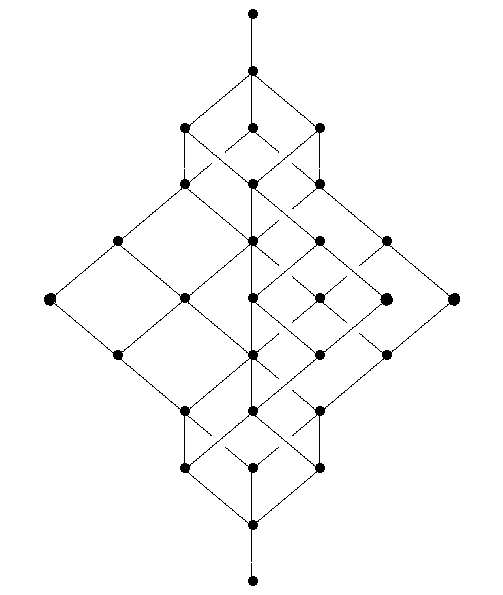
This picture makes it a bit hard to see the symmetry of the lattice, but if you look you can see it. (Can someone please draw a nice 3d picture that makes the symmetry manifest?)
If you look carefully here, as Hugh Thomas did, you will see 30 elements! That’s because the person who drew this picture, like me, defines a lattice to be a poset with upper bounds and lower bounds for all finite subsets. Dedekind defined it to be a poset with upper bounds and lower bounds for all nonempty finite subsets. In other words, Dedekind’s kind of lattice has operations and , while mine also has a top and bottom element. So, Dedekind’s ‘free lattice on 3 generators’ did not include the top and bottom element of the picture here. So, it had just 28 elements.
Now, there’s something funny about how 8-dimensional space and the number 28 are showing up here. After all, the dimension of is 28. This could be just a coincidence, but maybe not. Let me explain why.
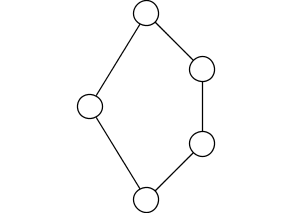
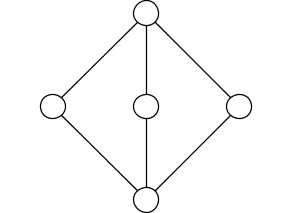
The 3 subspace problem asks us to classify triples of subspaces of a finite-dimensional vector space , up to invertible linear transformations of . There are finitely many possibilities, unlike the situation for the 4 subspace problem. One way to see this is to note that 3 subspaces give a representation of the quiver, which is this little category here:
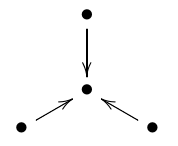
This fact is trivial: a representation of the quiver is just 3 linear maps , , , and here we are taking those to be inclusions. The nontrivial part is that indecomposable representations of any Dynkin quiver correspond in a natural one-to-one way with positive roots of the corresponding Lie algebra. The Lie algebra corresponding to is , the Lie algebra of the group of rotations in 8 dimensions. This Lie algebra has 12 positive roots. So, the quiver has 12 indecomposable representations. The representation coming from any triple of subspaces must be a direct sum of these indecomposable representations, so we can classify the possibilities and solve the 3 subspace problem!
What’s going on here? On the one hand, Dedekind the free modular lattice on 3 generators shows up as a lattice of subspaces generated by 3 subspaces of . On the other hand, the 3 subspace problem is closely connected to classifying representations of the quiver, whose corresponding Lie algebra happens to be . But what’s the relation between these two facts, if any?
Another way to put the question is this: what’s the relation between the 12 indecomposable representations of the quiver and the 28 elements of the free modular lattice on 3 generators? Or, more numerogically speaking: what relationship between the numbers 12 and 28 is at work in this business?
Here’s one somewhat wacky guess. The Lie algebra of has 12 positive roots, and its Cartan algebra has dimension 4. As usual, the Lie algebra is spanned by positive roots, an equal number of negative roots, and the Cartan subalgebra, so we get
But I don’t really see how this is connected to anything I’d said previously. In particular, I don’t see why 24 of the 28 elements of the lattice of subspaces generated by
should be related to roots of .
I think a more sane, non-numerological approach to this network of issues is to take the quiver representation corresponding to Dedekind’s choice of , decompose it into indecomposables, and see which positive roots those correspond to. I may try my hand at that in the comments, but I’m really looking for some help here.




Re: The Free Modular Lattice on 3 Generators
Here are the 12 indecomposable representations of the quiver. I’ll just write the dimensions of the vector spaces involved, and let you guess the maps between them — they’re not hard to guess with a few hints.
First there are 3 representations where the maps involved are not injective. These cannot show up inside a representation obtained from subspaces :
For the other representations the maps are injective: