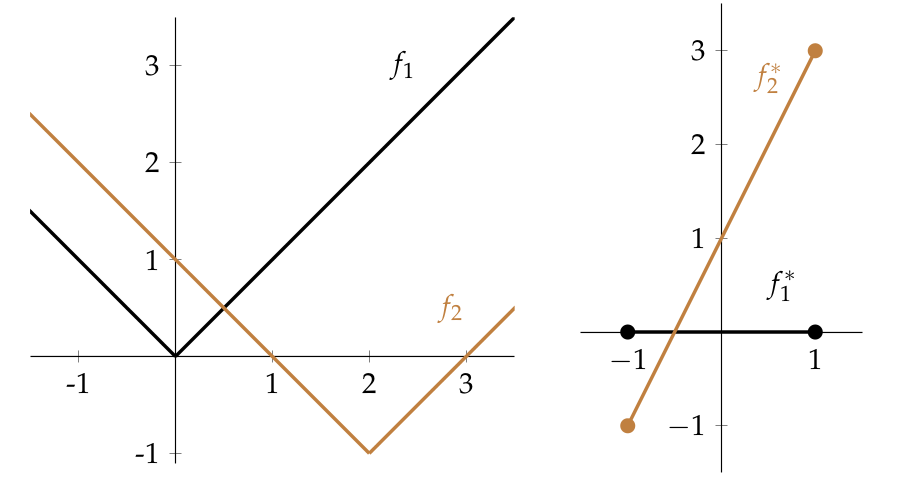May 25, 2014
Spans and the Categorified Heisenberg Algebra (Part 2)
Posted by John Baez
Last summer I gave a little course on something I really like: Jeffrey Morton and Jamie Vicary’s work on the ‘categorified Heisenberg algebra’ discovered by Mikhail Khovanov. It ties together combinatorics and the math of quantum theory in a fascinating way… related to nice old ideas, but revealing a new layer of structure. I blogged about that course here, with links to slides and references.
The last two weeks I was in Paris attending a workshop on operads. I learned a lot, and it was great to talk to Mathieu Anel, Steve Awodey, Benoit Fresse, Nicola Gambino, Ezra Getzler, Martin Hyland, André Joyal, Joachim Kock, Paul-André Melliès, Emily Riehl, Vladimir Voevodsky… and many other people to whom I apologize for not including in this prestigious list! (The great thing about senility is never having to say you’re sorry, but I haven’t quite reached that stage.)
There is a lot I could say… but that will have to wait for another time. For now I just want to point out this annotated video:
• Spans and the categorified Heisenberg algebra.
of a talk at the Catégories, Logiques, Etc… seminar at Paris 7, run by Anatole Khelif. This should be a fairly painless introduction to the subject, since I sensed that lots of people in the audience wanted me to start by explaining prerequisites: categorification, TQFTs, 2-Hilbert spaces and the Heisenberg algebra.
That means I didn’t manage to discuss other interesting things, like the definition of symmetric monoidal bicategory, or the role of combinatorics, especially Young diagrams. For those, go here and check out the links!

May 22, 2014
Enrichment and the Legendre-Fenchel Transform II
Posted by Simon Willerton
Last time, I described the Legendre-Fenchel transform. For a real vector space , the transform gives a bijection between the convex functions on and the convex functions on its dual . This time I’ll show how this is naturally an example of the profunctor nucleus construction in enriched category theory.
The key to this relationship is that the natural pairing between a vector space and its dual can be thought of as profunctor between discrete -categories, where is the extended real numbers thought of as a closed, symmetric monoidal category.
As I’ll explain, we can then apply the machinary of the nucleus construction to get a pair of maps between the -presheaves on , which just means the -valued functions on , and the -copresheaves, ie the -valued functions, on . Restricting to the part on which the pair of maps is bijective, we get that the transform gives a bijection between the respective sets of convex functions.
This category theoretic treatment gives us a little more than the standard treatment. Usually people put an ordering on the functions and observe that Legendre-Fenchel transform is order reversing. The category theory tells us that we can refine this and put a generalized, generalized metric space structure on the space of functions so that the transform is distance non-increasing, and is in fact distance preserving in the case of convex functions. This is illustrated by the above picture, as we will discover below!
May 20, 2014
Classifying by Generalizing: The Theory of Accessibility Relative to a Limit Doctrine
Posted by Emily Riehl
Guest post by Tim Campion
In the tenth installment of the Kan Extension Seminar, we take a break from all the 2-category theory we’ve been doing, in favor of some good old-fashioned 1-category theory (although if you keep an eye out, you may notice some higher dimensions lurking in the background!). This week’s paper is A Classification of Accessible Categories by Adámek, Borceux, Lack, and Rosický, which both generalizes and refines the classical theory of locally presentable and accessible categories by working relative to a new parameter, , called a limit doctrine. But don’t worry if you know nothing about locally presentable and accessible categories – I hope this post can serve as an introduction, from the -relative perspective.
The classical theory of locally presentable and accessible categories is notable partly because of its scope: many categories of intrinsic mathematical interest – from groups, rings, and fields, to categories themselves, to Banach spaces and contractive maps – are accessible. At the same time, the theory is notable for the richness of the categorical concepts that it brings together – from colimit completions, to sketches, to orthogonality classes. Both of these aspects will also be apparent in the generalized theory. We will recover, for example, not only the notion of a (multi sorted) Lawvere theory, but also much of the theory surrounding it.
I’d like to thank all my fellow seminar participants for thoughtful discussions so far, as well as everyone who’s joined the discussion at the Café. It’s been a fantastic experience , “popping open” the vacuum in which I’ve done category theory in the past! A special thanks to Emily for organizing all of this and providing feedback and support, and to Joe Hannon for what’s been a fruitful reading collaboration.
May 14, 2014
Categories vs. Algebras
Posted by Tom Leinster
Representation theorists make good use of the “category algebra” construction. This is a way of turning a linear category (one whose hom-sets are vector spaces) into an associative algebra. In this post, I’ll describe what the category algebra is and why it seems to be important.
I’ll also ask two basic questions about the category algebra construction. I hope someone can tell me the answers.
 Posts with this logo use
Posts with this logo use