August 22, 2013
Linear Operators Done Right
Posted by Tom Leinster
A conversation prompted by Simon’s last post reminded me of an analogy that’s too excellent to be buried in a comments thread. It must be very well-known, but I’ll go ahead and describe it anyway.
The analogy is between complex numbers and linear operators on an inner product space. Its best feature is that it makes important properties of complex numbers correspond to important properties of operators:
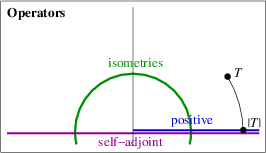
The title of this post refers to Sheldon Axler’s beautiful book Linear Algebra Done Right, which I’ve written about before. Most of what I’ll say can be found in Chapter 7. It’s one of those texts that feels like a piece of category theory even though it’s not actually about categories.
August 19, 2013
The Nucleus of a Profunctor: Some Categorified Linear Algebra
Posted by Simon Willerton
Most of us learnt as undergraduates that from an -matrix you get two linear maps and , and that these are adjoint with respect to the standard inner products on and : I want to explain how I think of (at least part of) an enriched category construction, the nucleus of a profunctor, as being analogous. I learnt about the nucleus idea in a recent paper by Dusko Pavlovic.
Quantitiative Concept Analysis, in Formal Concept Analysis, Lecture Notes in Computer Science, Volume 7278 (2012) 260–277; also arxiv:1204.5802
The construction does seem to have been described before for categories enriched over quantales in the following paper, but I don’t know if it’s known in the category theoretic community at large.
Javier Gutiérrez García, Iraide Mardones-Pérez, María Angeles de Prada Vicente, and Dexue Zhang, Fuzzy Galois connections categorically, Mathematical Logic Quarterly 56, No. 2, 131–147 (2010).
Let’s fix a suitable category to enrich over. Pick if you are more comfortable with ordinary categories, so that a -category is just an ordinary small category.
The analogue of a matrix in the world of -categories is a profunctor . This gives rise to two -functors and which are adjoint What we will actually be interested in the nucleus, which is the centre, or invariant part, of this adjunction. In the linear algebra world, the analogue of this is the fixed point set of or equivalently the fixed point set of . Rather naughtily, I won’t motivate the construction in this post, but in the next post, hopefully, I will discuss Formal (and Fuzzy) Concept Analysis and describe what this has to do with it.
The observant amongst you might have observed that this is a generalization of the Isbell completion of a category which I have mentioned here before. In that case you work with the identity profunctor, .
August 18, 2013
The Shannon Capacity of a Graph, 2
Posted by Tom Leinster
Graph theorists have many measures of how ‘big’ a graph is: order, size, diameter, radius, circumference, girth, chromatic number, and so on. Last time I told you about two of them: independence number and Shannon capacity. This time I’ll bring in two other measures of size that I’ve written about previously in contexts other than graph theory: maximum diversity and magnitude.
The post will end not with a bang, but a whimper. Although there’s something simple and clean to say about the connection between maximum diversity and standard graph invariants, the relationship with magnitude is much more mysterious, and I don’t have much more to say than ‘what’s going on?’. So there will be no satisfying conclusion. Consider yourself warned!
August 15, 2013
Oxford Workshop in Quantum Mathematics and Computation
Posted by Simon Willerton
Guest post by Bruce Bartlett
The newly-created Centre for Quantum Mathematics and Computation (QMAC) at the University of Oxford is holding an inaugural research workshop from October 1-4, 2013, and you are invited to attend.

The workshop will have plenary talks by Steve Awodey, John Baez, Alexander Beilinson, Lucien Hardy, Martin Hyland, Dana Scott, Vladimir Voevodsky, and Anton Zeilinger, along with contributed talks and a problem session.
The workshop is one of four Clay Research Workshops occurring in Oxford that week (including one on Number Theory and Physics, and one on Computational Intractability) along with the Clay Research Conference and the conference celebrating the opening of the new Oxford Mathematics building.
A link for registration is available at the QMAC Workshop webpage. There are also webpages on the Clay Research Conference and the New Mathematics Building Opening Conference.
The workshop is funded by the Clay Mathematics Institute and the Engineering and Physical Sciences Research Council.
Inquiries regarding the workshop may be directed to Chris Douglas at cdouglas@maths.ox.ac.uk.
August 10, 2013
The Shannon Capacity of a Graph, 1
Posted by Tom Leinster
You’ve probably had the experience where you spell your name or address down the phone, and the person on the other end mistakes one letter for another that sounds similar: P sounds like B, which is easily mistaken for V, and so on. Under those circumstances, how can one most efficiently communicate without risk of error?
Shannon found the answer, but this isn’t part of his most famous work on communication down a noisy channel. There, the alphabet has no structure: any substitution of letters is as likely as any other. Here, the alphabet has the structure of a graph.
Today, I’ll explain Shannon’s answer. Next time, I’ll explain how it’s connected to the concept of maximum diversity, and thereby to magnitude.
August 4, 2013
What is a Spectral Sequence?
Posted by Mike Shulman
I’ll probably be posting a lot less frequently for a while, as I now have something else to occupy my time: my son Arthur was born last week! But I’ve been working on this post for a while, so I wanted to get it out.
I’m a category theorist at heart (although it’s getting to the point where I can start calling myself a homotopy type theorist too). But my advisor, Peter May, is an algebraic topologist (with categorical leanings), so I sat in on a lot of algebric topology lectures as a grad student. And always, one of the most mystifying things in algebraic topology to me was the notion of a spectral sequence. All the topologists loved them as a calculational tool, but I never felt as though I had any conceptual understanding of what they meant, and without that I wasn’t really able to motivate myself to learn to calculate with them.
Recently, however, I acquired a new motivation: homotopy type theory is rapidly pushing up against the boundaries of algebro-topological calculations that can be done classically without spectral sequences, so it started to feel somewhat urgent that we get some idea of whether spectral sequences exist in HoTT. After whacking my head against this problem for a bit, I think I can provisionally answer that yes, they do. Moreover, this process of whacking my head has finally jarred something loose, so that I now have an answer to the question “what is a spectral sequence?” that’s at least more satisfying to me that anything I’d come up with before. I expect that it’s “well-known to the people who know it”, but I haven’t seen it written out it just this way before.
In this post I’m going to explain this answer. Like most explanations of spectral sequences, it focuses on a particular spectral sequence; in this case, the spectral sequence of a tower of fibrations (of spaces or spectra). No homotopy type theory is required, although anyone who’s read through Chapter 8 of the HoTT Book ought to be able to translate into HoTT pretty easily. In a companion post at the HoTT blog, I’ll explain how to deduce the Atiyah-Hirzebruch and Serre spectral sequences, and hopefully give a taste of what they can do for us.
August 3, 2013
Integral Octonions (Part 4)
Posted by John Baez
This mini-series will take a break soon, since I’ll be wandering around China from August 6th to 20th. But before I go, I’d like to say a bit about the 8-dimensional polytope whose vertices are the 240 integral octonions with smallest norm (apart from zero)—or if you prefer, the 240 root vectors of .
August 1, 2013
Spans and the Categorified Heisenberg Algebra
Posted by John Baez
There’s a nice conference coming up soon in the wild west of China:
- Higher Structures in China IV, Lanzhou University, August 14-16, 2013, organized by Li Guo, Yanfeng Luo, Weiwei Pan, Yunhe Sheng and Chenchang Zhu.
Chongying Dong is giving a short course on quantum dimensions for vertex operator algebra representations, and quantum Galois theory. Pierre-Louis Curien will give one on higher-dimensional rewriting and applications to coherent presentations of Artin groups. And I’ll give one about spans of groupoids and the combinatorics underlying the key relation in the Heisenberg algebra:
Besides talking about these topics, which form a nice example of categorified algebra, I thought this would be a good chance to familiarize more people with the second column of the periodic table:
- bicategories
- monoidal bicategories
- braided monoidal bicategories
- sylleptic monoidal bicategories
- symmetric monoidal bicategories
So, I’ll use Mike Stay’s wonderful diagrams to explain these things. You can see my slides here.
 Posts with this logo use
Posts with this logo use 















