Spans and the Categorified Heisenberg Algebra
Posted by John Baez
There’s a nice conference coming up soon in the wild west of China:
- Higher Structures in China IV, Lanzhou University, August 14-16, 2013, organized by Li Guo, Yanfeng Luo, Weiwei Pan, Yunhe Sheng and Chenchang Zhu.
Chongying Dong is giving a short course on quantum dimensions for vertex operator algebra representations, and quantum Galois theory. Pierre-Louis Curien will give one on higher-dimensional rewriting and applications to coherent presentations of Artin groups. And I’ll give one about spans of groupoids and the combinatorics underlying the key relation in the Heisenberg algebra:
Besides talking about these topics, which form a nice example of categorified algebra, I thought this would be a good chance to familiarize more people with the second column of the periodic table:
- bicategories
- monoidal bicategories
- braided monoidal bicategories
- sylleptic monoidal bicategories
- symmetric monoidal bicategories
So, I’ll use Mike Stay’s wonderful diagrams to explain these things. You can see my slides here.
Heisenberg reinvented matrices while discovering quantum mechanics, and the algebra generated by annihilation and creation operators and obeying
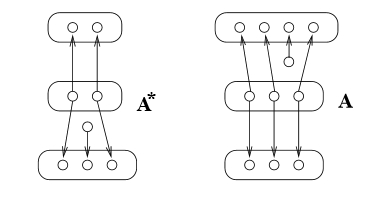
was named after him: the Heisenberg algebra. It turns out that matrices arise naturally from ‘spans’, where a span between two objects is just a third object with maps to both those two:

Spans also let you formalize the simple combinatorial interpretation of the equation , namely,
there’s 1 more way to add an element to a set and then remove one than to remove one and then add one.
More recently, Mikhail Khovanov introduced a ‘categorified’ Heisenberg algebra, where this equation holds only up to isomorphism, and this isomorphism obeys new relations of its own.
The meaning of these new relations was initially rather mysterious, at least to me. However, Jeffrey Morton and Jamie Vicary have shown that these, too, have a nice interpretation in terms of spans. We can begin to formalize this using the work of Alex Hoffnung and Mike Stay, who have shown that spans of groupoids are morphisms in a symmetric monoidal bicategory.
Here are the slides:
• Part 1 – How Jeffrey Morton and Jamie Vicary categorified the Heisenberg algebra using spans of groupoids.
• Part 2 – The definition of symmetric monoidal bicategory, following Mike Stay.
• Part 3 – How the categorified Heisenberg algebra shows up in the theory of Young diagrams and Schur functors.

For more on this subject try these papers:
- Mikhail Khovanov, Heisenberg algebra and a graphical calculus.
- Jeffrey Morton and Jamie Vicary, The categorified Heisenberg algebra I: a combinatorial representation.
- Alex Hoffnung, Spans in 2-categories: a monoidal tricategory.
- Mike Stay, Compact closed bicategories.
- Jeffrey Morton, 2-vector spaces and groupoids.
- Jeffrey Morton, Categorified algebra and quantum mechanics.
- John Baez, Alex Hoffnung and Christopher Walker, Higher-dimensional algebra VII: groupoidification.
- John Baez and James Dolan, From finite sets to Feynman diagrams.
For more on the physics of spans, try this other talk of mine:
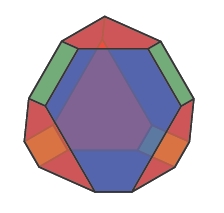
The pictures of creation and annihilation spans above are by Jeffrey Morton. The truncated shuffle polytope, a coherence law in the definition of braided monoidal bicategory, was drawn by Mike Stay. The Young diagrams with arrows showing the action of the categorified creation operator were drawn by Jeffrey Morton and Jamie Vicary.


Re: Spans and the Categorified Heisenberg Algebra
Parts 2 & 3 are dead links.