Compact Closed Bicategories
Posted by John Baez
I’m happy to announce that this paper has been published:
- Mike Stay, Compact closed bicategories, Theory and Applications of Categories 31 (2016), 755–798.
Abstract. A compact closed bicategory is a symmetric monoidal bicategory where every object is equipped with a weak dual. The unit and counit satisfy the usual ‘zig-zag’ identities of a compact closed category only up to natural isomorphism, and the isomorphism is subject to a coherence law. We give several examples of compact closed bicategories, then review previous work. In particular, Day and Street defined compact closed bicategories indirectly via Gray monoids and then appealed to a coherence theorem to extend the concept to bicategories; we restate the definition directly.
We prove that given a 2-category with finite products and weak pullbacks, the bicategory of objects of , spans, and isomorphism classes of maps of spans is compact closed. As corollaries, the bicategory of spans of sets and certain bicategories of ‘resistor networks” are compact closed.
This paper is dear to my heart because it forms part of Mike Stay’s thesis, for which I served as co-advisor. And it’s especially so because his proof that objects, spans, and maps-of-spans in a suitable 2-category forms a compact symmetric monoidal bicategory turned out to be much harder than either of us were prepared for!
A problem worthy of attack
Proves its worth by fighting back.
In a compact closed category every object comes with morphisms called the ‘cap’ and ‘cup’, obeying the ‘zig-zag identities’. For example, in the category where morphisms are 2d cobordisms, the zig-zag identities say this:
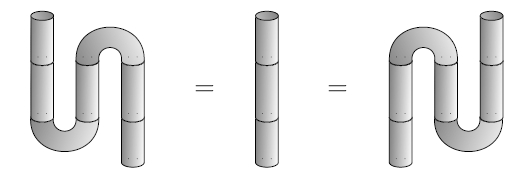
But in a compact closed bicategory the zig-zag identities hold only up to 2-morphisms, which in turn must obey equations of their own: the ‘swallowtail identities’. As the name hints, these are connected to the swallowtail singularity, which is part of René Thom’s classification of catastrophes. This in turn is part of a deep and not yet fully worked out connection between singularity theory and coherence laws for ‘-categories with duals’.
But never mind that: my point is that proving the swallowtail identities for a bicategory of spans in a 2-category turned out to be much harder than expected. Luckily Mike rose to the challenge, as you’ll see in this paper!
This paper is also gaining a bit of popularity for its beautiful depictions of the coherence laws for a symmetric monoidal bicategory. And symmetric monoidal bicategories are starting to acquire interesting applications.
The most developed of these are in mathematical physics — for example, 3d topological quantum field theory! To understand 3d TQFTs, we need to understand the symmetric monoidal bicategory where objects are collections of circles, morphisms are 2d cobordisms, and 2-morphisms are 3d cobordisms-between-cobordisms. The whole business of ‘modular tensor categories’ is immensely clarified by this approach. And that’s what this series of papers, still underway, is all about:
Bruce Bartlett, Christopher L. Douglas, Christopher J. Schommer-Pries and Jamie Vicary, Extended 3-dimensional bordism as the theory of modular objects.
Bruce Bartlett, Christopher L. Douglas, Christopher J. Schommer-Pries and Jamie Vicary, Modular categories as representations of the 3-dimensional bordism 2-category.
Mike Stay, on the other hand, is working on applications to computer science. That’s always been his focus — indeed, his Ph.D. was not in math but computer science. You can get a little taste here:
- Mike Stay and Jamie Vicary, Bicategorical semantics for nondeterministic computation, Proceedings of Mathematical Foundations of Programming Semantics 29 (2013), 345–359.
But there’s a lot more coming soon from him and Greg Meredith.
As for me, I’ve been working on applied math lately, like bicategories where the morphisms are electrical circuits, or Markov processes, or chemical reaction networks. These are, in fact, also compact closed symmetric monoidal bicategories, and my student Kenny Courser is exploring that aspect.
Basically, whenever you have diagrams that you can stick together to form new diagrams, and processes that turn one diagram into another, there’s a good chance you’re dealing with a symmetric monoidal bicategory! And if you’re also allowed to ‘bend wires’ in your diagrams to turn inputs into outputs and vice versa, it’s probably compact closed. So these are fundamental structures — and it’s great that Mike’s paper on them is finally published.

Re: Compact Closed Bicategories
Congratulations, Mike!
Anyone looking for hints about this, a wide-ranging discussion occurred on this blog almost 10 years ago.