December 31, 2006
Puzzle #11
Posted by John Baez
Happy New Year! Here’s a little puzzle to start the year off…
When was the toothpick invented?
December 26, 2006
This Week’s Finds in Mathematical Physics (Week 243)
Posted by John Baez
In week243 of This Week’s Finds, hear about Claude Shannon, his sidekick Kelly, and how they used information theory to make money at casinos and the stock market. Hear about the new book Fearless Symmetry, which explains fancy number theory to ordinary mortals. Learn about the Dark Ages of our Universe, and how they were ended by the earliest stars. And finally, get a taste of Derek Wise’s work on Cartan geometry, gravity… and hamsters!
December 25, 2006
The Earliest Stars?
Posted by John Baez
You may have read about this in the news, but here are the original articles:
- A. Kashlinsky, R. G. Arendt, J. Mather and S. H. Moseley, New measurements of cosmic infrared background fluctuations from early epochs, to appear in Ap. J. Letters.
- A. Kashlinsky, R. G. Arendt, J. Mather and S. H. Moseley, On the nature of the sources of the cosmic infrared background, to appear in Ap. J. Letters.
Executive summary: using delicate techniques to carefully sift through the infrared background radiation, the authors claim to find radiation not accounted for by previously known sources. Assuming the now-standard ΛCDM cosmology, the sources of this radiation date back to less than 1 billion years after the Big Bang, and were individually much brighter than current-day stars.
December 24, 2006
arXiv Policy Statement?
Posted by John Baez
A while back David Corfield raised some important issues about the academic commons. Here’s a practical question along those lines:
Does the arXiv have an official policy statement someplace where they promise to keep papers there freely available? They should. I haven’t been able to find one! Did I miss it?
Marco Grandis raised this issue in a post to the category theory mailing list.
Puzzle #9
Posted by John Baez
Which famous philosopher is also known as the RaMBaM?
December 21, 2006
Conference: Lie Algebroids and Lie Groupoids in Differential Geometry
Posted by Urs Schreiber
In October 2007 there will be a four-day conference in Sheffield on Lie algebroids and Lie groupoids in Differential Geometry, organized by Kirill Mackenzie and Ieke Moerdijk.
Lectures on Classical Mechanics
Posted by John Baez
In the Spring of 2005 I taught a graduate course on classical mechanics, and Derek Wise took beautifully precise notes. I started with the Lagrangian approach, with a heavy emphasis on action principles, and derived the Hamiltonian approach from that.
Now, as a Christmas present to the world, Blair Smith has converted them into a beautiful typeset PDF document, adding extra material:
- John Baez, Blair Smith and Derek Wise, Lectures on Classical Mechanics. Also available in Postscript format.
Enjoy! And, please report any typos or other errors that you find!
A Little Bit of Geometric Langlands: Relation to Integrable Systems
Posted by Urs Schreiber
As I mentioned in Navigating Geometric Langlands by Analogies, the mathematicians and the string theorists in Hamburg have a a small series of lectures this term, where we try to explain to each other some tiny fraction of what Langlands duality is about.
Last time we had something on the “classical” number-theoretic aspect. I didn’t even try to report on that.
This time, Jörg Teschner spoke about geometric Langlands duality. After briefly mentioning what the main statement is, he concentrated on understanding one aspect of this statement using the language of integrable systems.
Ever since it was found that certain aspects of super Yang-Mills theory are governed by what are called quantum integrable systems, and due to the impact this has on understanding and testing the AdS/CFT duality, string theorists have been interested in integrable systems. That’s one reason why Jörg Teschner decided to emphasize this aspect of the talk.
Roughly, the main point he tried to make could maybe be summarized like this:
The geometric Langlands duality relates (conjecturally) two different derived categories by an equivalence.
But on top of that, the conjecture states that both these derived categories have something like a nice “basis of eigenstates of some operator” (compare my previous entry # on what such a statement would really mean) and that under the equivalence a basis vector on one side is sent to a basis vector on the other.
Now, on one of these two sides, those “basis vectors” (the Hecke eigensheaves) can be understood as coming from common eigenstates of the set of commuting Hamiltonians of some integrable system.
From this point of view of integrable systems, geometric Langlands duality seems to be a statement about when and how an integrable system admits a separation of variables.
If you like integrable systems, that should be interesting.
Common Applications
Posted by David Corfield
I’ve been reading some of Jorg Lemm’s papers in recent days. He’s written a book - Bayesian Field Theory - which I don’t have access to, but he had written a paper of the same name earlier. In it (page 6, note 1) he remarks that:
statistical field theories, which encompass quantum mechanics and quantum field theory in their Euclidean formulation, are technically similar to a nonparametric Bayesian approach.
It is intriguing to see so many constructions of mathematical physics - mean field methods, diffusion models, free energy - find a use in learning theory. But what to make of it? If we think it needs an explanation at all, we might say that perhaps it’s telling us that we only have a limited number of tools, so should expect to use them time and again. If we were washed up on a desert island with just a knife in our pocket, we’d find a host of uses for it, with little in common between them, e.g., opening a clam and sharpening a stick.
David Ruelle favoured this kind of explanation about multiple application in “Is our mathematics natural? The case of equilibrium statistical mechanics.” Bull. Amer. Math. Soc. 19, 259-268 (1988). Our minds have a limited repertoire, which explains why mathematicians keep bumping into the same constructions. Closer to this blog, a similar question is why the deeper reaches of number theory (Langlands programme) and quantum field theory (duality) are so closely related. In Mathematics in the 20th Century, Michael Atiyah’s predictions for the 21st century went thus:
What about the 21st century? I have said the 21st century might be the era of quantum mathematics or, if you like, of infinite dimensional mathematics. What could this mean? Quantum mathematics could mean, if we get that far, ‘understanding properly the analysis, geometry, topology, algebra of various non-linear function spaces’, and by ‘understanding properly’ I mean understanding it in such a way as to get quite rigorous proofs of all the beautiful things the physicists have been speculating about.
Quantization and Cohomology (Week 9)
Posted by John Baez
Here are the final notes from my Fall 2006 course on Quantization and Cohomology:
- Week 9 (Dec. 5) - A glimpse of what’s to come. Phases versus relative phases. Geometric quantization: finding a connection on a U(1) bundle whose curvature is the symplectic 2-form ω on phase space. Why doing this is only possible if ω defines an integral cohomology class - hence the term ‘quantization’.
Last week’s notes are here; the notes from next quarter begin here.
My colleague Apoorva Khare has produced a LaTeX version of the notes for the entire Fall quarter, and Christine Dantas has drawn figures for these notes. The notes still need more polishing, but they’re already very useful:
- John Baez and Apoorva Khare, with figures by Christine Dantas, Course Notes on Quantization and Cohomology, Fall 2006. Also available in Postscript.
December 20, 2006
Excellent Math in Bonn: Opening Colloquium in January
Posted by Urs Schreiber
After decades in which every potential sign of elitism was oficially frowned upon, the last German government had decided that it was quite a pity that every university here was and had to be equal, with none being more equal than the others. They decided it would be lots of fun to have some elite universities, like all those other countries do. So they decided to find them – by decree.
The result is that, as of recently, two Munich universities as well as that in Karlsruhe are officially elite universities™. In addition, a couple of institutes of several other universities, in various fields, have been declared to be clusters of excellence™.
In practice, what this really means is that those places with the new titles will get extra government money from now on. Everybody is excited about that.
Anyway, there is now precisely one “cluster of excellence” concerned with mathematics in Germany, and that’s in Bonn.
Hausdorff Center for Mathematics
As a cluster of excellence, it’s titled
Mathematics: Foundations, Models, Applications.
Luckily, that title is not too restrictive.
I am writing all this because you might be intersted in the cluster’s Opening Colloquium that takes place January 19th and 20th, 2007.
Plenary lectures will be given by
Douglas Arnold (Minneapolis)
Michael Hopkins (Harvard)
Elliott Lieb (Princeton)
László Lovász (Budapest)
Andreu Mas-Colell (Barcelona)
Wendelin Werner (Paris)
So it might be worth a visit.
Research Blogging
Posted by Urs Schreiber
Clifford Johnson ponders the advantages of research blogging in The Blog as a Sharp Tool for Research and now again in Research Blogging.
Related considerations were voiced by Craig Laughton early this year: Exploring the Blogosphere.
I don’t have much to add to that, except for noting that I used blogging in this sense, and almost exclusively in this sense, from the very beginning.
And I’d guess that, long long before my feeble writings, John’s TWFs served a similar purpose.
One big difference is that Clifford Johnson has a non-public blog for his research, which, as he writes #
[…] is also the place where everyone (including me) can say silly things and ask silly questions if we want to, without the whole world watching. That latter is a very important feature, in fact.
For some reason I have always felt like moving private discussions on technical issues out in the open. For me that’s a matter of increasing the reaction rate of research by increasing the reaction surface. And, looking back, it did work for me #.
With the esoteric stuff we are talking about, this seems more important to me than shielding away insights and hiding mistakes. The game here is not Bingo #.
But I am aware that most people feel quite different about this – and quite possibly for good reasons. But I cannot help it. On the other hand, I am fond of having found philosophical support # # from David Corfield.
While I cannot prove it, I think everybody would benefit from seeing more research-related communication done out in the open. The most valuable aspect of many conferences is the conversation one has in between the talks. And this kind of conversation is what I am after.
December 18, 2006
Universal Gerbes
Posted by Urs Schreiber
Jim Stasheff asked me to forward the following question to the -Café audience:
There is a universal principal bundle for any group. Is there also a universal gerbe?
This Week’s Finds in Mathematical Physics (Week 242)
Posted by John Baez
In week242 of This Week’s Finds, see some incredible photos of Saturn’s rings taken by the Cassini spacecraft:

Hear about some of the other exciting space missions NASA may cancel to pay for an expensive plan to send canned primates to Mars. See the Sun in neutrinos. And learn about Jeffrey Morton’s new approach to topological quantum field theory using a double bicategory of cobordisms with corners!
December 15, 2006
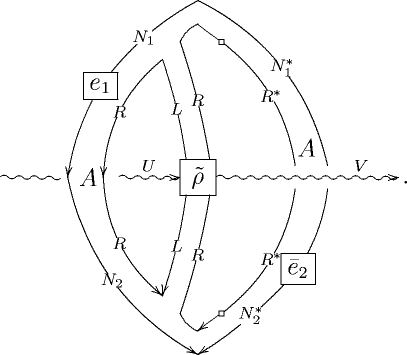
Frobenius Algebroids with Invertible Products
Posted by Urs Schreiber
Sometimes, banalities fool us into ignoring important structure. That happens when the banality is the degenerate case of something that is in general more interesting.
One banality is this.
An associative monoidoid (I mean any enriched category, please see the comments below)
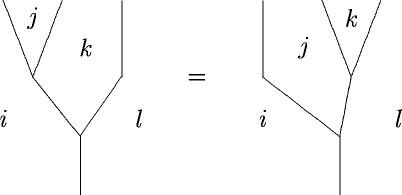
with invertible product (this invertibility is the degeneracy)
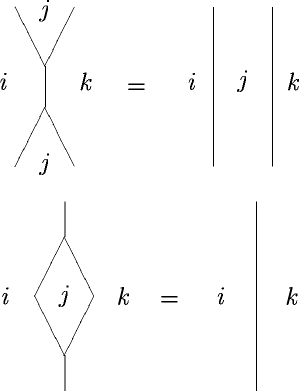
is naturally a Frobenius monoidoid
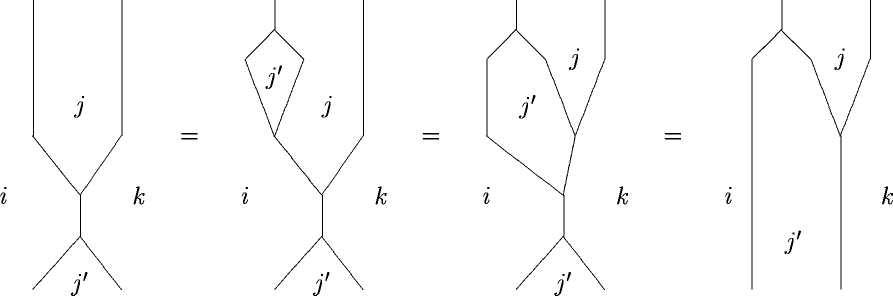
only that you would tend to ignore this fact. It’s like ordering Pizza Tonno without Tuna.
December 14, 2006
Higher Categories at the Fields Institute
Posted by John Baez
Excitement is building throughout Toronto as news of this workshop spreads:
- Higher Categories and Their Applications, January 9-13, 2007, part of the Thematic Program in Geometric Applications of Homotopy Theory at the Fields Institute.
Crowds are lining up in front of the Fields Institute, trying to get seats early, wondering when the show will start. To prevent rioting and looting, I have decided to post a tentative schedule including abstracts of some of the talks.
December 13, 2006
Back from NIPS 2006
Posted by David Corfield
Aside from thinking up the second n-Café millennium prize, there wasn’t much time for higher-dimensional algebra last week while I attended the NIPS 2006 machine learning conference/workshop in Vancouver/Whistler. To find a role even for ordinary category theory in machine learning presents an interesting challenge. Most of what I’ve seen relates to neural networks, e.g., here.
Now, it looked as though neural networks had had their day, superseded by kernel methods, both support vector machines (SVMs) and Gaussian processes (GPs), as used by most of the people I work with in Tübingen. But there’s been a recent revival of interest in neural networks with the discovery of a new way to train deep networks, as Yoshua Bengio described.
Bicat is Not Triequivalent to Gray
Posted by David Corfield
Bicat is the tricategory of bicategories, homomorphisms, pseudonatural transformations, and modifications. Gray is the subtricategory of 2-categories, 2-functors, pseudonatural transformations, and modifications. We show that these two tricategories are not triequivalent.
Communicating Thoughts on the Web
Posted by Urs Schreiber
In school, I remember, I got very upset when somebody once tried to teach me that no thinking is possible without language. While I think (with or without language?) that this is clearly wrong, it is clearly right that language greatly affects – and good language greatly facilitates – thinking.
Thinking without language is possible, but it is like computing without RAM: it is hard to think a complex thought without the ability of saving big sub-thoughts using a convenient address: a word. Or an equation. Or a diagram. Or a word for an equation or a diagram.
Even with lots of language, thinking just by yourself may be inefficient. Many a thought wants to be communicated and recycled once or twice until reaches a desireable form. At least for me, a blog like the one we are running here is a means to greatly increase the potential for thought exchange.
That requires language. And good language. In our business this means: it requires good means to express math on the web. s One of the marvelous things of this blog, for me, is the sophistication its administrator, Jacques Distler, has put and is putting into web-based math technology. I imagine that in a few years using equations and diagrams in electronic communication will be no less unusual than discussion with your colleagues in front of your office’s blackboard. But somebody has to make it real.
And it’s not as trivial as one might wish it were. It’s rather an entire research all in itself. Check out Jacques’s report on a conference Evolution of Mathematical Communication, where he gave a talk on on Blogging with MathML.
MathML is the communication protocol for electronic mathematical expressions that is at work behind the scenes when we transmit thoughts like
in -Café-communication.
Interestingly, as Jacques mentioned in his talk, the discussion that is archived on the three blogs hosted by him, his own Musings, as well as the (now somewhat dormant) String Coffee Table and the -Category Café here, now constitutes one of the largest collections of MathML on the web.
While I find nothing more convenient than being able to include proper LaTeX in everything I write here, with the output seamlessly embedded into everything else, there are still some technological hurdles that want eventually to be removed.
One is on the server side. The reason that there are so few weblogs with full WebTeX/MathML support like here becomes quite apparent once you follow Jacques’ frequent accounts on what kinds of problems he had to solve to make it work.
As a result, other scientific blogs, whose owners feel the desire of transmitting a formula over the web once in a while, try to resort to solutions like mimeTeX, as for instance Clifford Johnson over at Asymptotia did now.
It’s not at me to discuss the pros and cons of these different solutions in detail. All I’ll notice here is that most solutions I know so far have the one big drawback that they are restricted to a fixed subset of LaTeX. They won’t allow you to load your own packages. In particular, this means: little support for diagrams.
But, in this respect, mimeTeX has at least a slight advantage: it does allow picture environments. While not the same as things like xypic, this does allow to communicate thoughts of this form
by typing the relevant LaTex directly (more or less) inline with the surrounding text. See the mimeTeX site for how to do this, if you want to use it here.
Of course there is always the, in a way, most primitive option: simply compile your LaTeX on your own machine as usual, convert it to a pdf and link to that. As John remarked recently (I cannot find the comment right now) this is, while by itself perfectly fine, for some funny psychological reason not as vivid a communication technique as having the LaTeX output directly on the web page.
To get that, of course, you can always turn the LaTeX output into gif and include that directly using the img tag.
To see the difference, notice that the following example will inevitably attract your attention, while you will probably have ignored this diagram - and its explanation - when I first linked to the pdf it appeared in #
You can do all this gif-conversion by hand, if you know how to. But there is also a little script freely available online, which facilitates and automates the task a little: TeX to GIF.
December 12, 2006
Navigating Geometric Langlands by Analogies
Posted by Urs Schreiber
On occasion of the new paper by Gukov-Witten on further details of how the geometric Langlands duality can be understood as a special case of S-duality in 4-dimensional Yang-Mills theory or, equivalently, of Mirror-symmetry of the 2-dimensional field theory obtained from that by compactification, I would like to recall some – analogies.
No, I am not an expert on geometric Langlands, and I haven’t even learned (mostly from Tony Pantev I, II and Anton Kapustin I, II, III) more than the most basic statements involved. Usually, talking about Langlands duality, classical or geometric, quickly leads to ever and ever more sophisticated constructions. It’s heavy machinery taken to its extreme.
But usually, if something is exceptionally interesting it is so not because it is arbitrarily convoluted and that being it – but because governing all that complexity is a single elegant mechanism.
Exactly that seems to be true for geometric Langlands, including its connection to quantum field theory. And it ought to be emphasized a little more.
We have a seminar here in Hamburg this semester, where the mathematicians join forces with the string theorists in the hope of teaching each other a tiny little bit of what geometric Langlands is about. In order to prepare myself for that, I want to start rather leisurely by simply recalling some analogies and simple pictures that should help discern the underlying basic structure.
December 8, 2006
Local Transition of Transport, Anafunctors and Descent of n-Functors
Posted by Urs Schreiber
In discussion here we discovered that we need to harmonize our use of the terms in the title of this post. Here is my take at what is going on. Please feel free to add your comment and correct me where I need correction.
December 7, 2006
New Light Particle(s) Discovered?
Posted by John Baez
The lightest known particle heavier than the electron is the muon: it’s about 207 times as heavy. This paper claims to have found evidence for new neutral particles that are only about 14 and 37 times as heavy as the the electron:
- Piyare Lal Jain and Gumurkh Singh, Search for new light particles decaying into electron pairs of mass below 100 MeV/c2, Jour. Phys. G: Nuclear and Particle Physics 34 (2007), 129-138.
Here’s a news story:
The title of this story makes the discovery sound like a sure thing, but I think we should be careful. The evidence is not iron-clad — and particle physics beyond the Standard Model is serious stuff!
December 6, 2006
Guiraud on Higher-Dimensional Rewrite Rules
Posted by John Baez
In this quarter’s last class on Classical versus Quantum Computation, I hinted that one could use 3-dimensional structures to understand the process of computation. A key figure in this line of work is Yves Guiraud, and he just put some of his papers on this topic on the arXiv:
- Yves Guiraud, Termination orders for 3-dimensional rewriting, Journal of Pure and Applied Algebra 207 (2006), 341-371.
- Yves Guiraud, Termination orders for 3-polygraphs, Comptes-Rendus de l’Academie des Sciences Serie I, 342 (2006), 219-222.
- Yves Guiraud, Two polygraphic presentations of Petri nets, Theoretical Computer Science 360 (2006), 124-146.
- Yves Guiraud, The three dimensions of proofs, Annals of Pure and Applied Logic 141 (2006), 266-295.
December 5, 2006
Talks at “Higher Categories and their Applications”
Posted by Urs Schreiber
In the context of the workshop Higher Categories and their Applications that takes place at the Fields Institute next January, I am invited to give two talks, one on categorical and 2-categorical aspects of 2-dimensional quantum field theory, the other on higher parallel transport.
In order to harmonize this with other talks being given, I was asked to indicate what I might and might not mention. For those interested, here is some discussion.
A preliminary schedule and some of the abstracts can now be found here.
Postdoctoral Position at the Interface of Algebra, Conformal Field Theory and String Theory
Posted by Urs Schreiber
The Mathematics Department of the University of Hamburg has a postdoctoral position available in the area of Algebra, Conformal Field Theory and String Theory which is part of the Collaborative Research Centre 676 “Particles, Strings and the Early Universe: the Structure of Matter and Space-Time” funded by the German Science Foundation (DFG).
The position starts in the fall of 2007 and is for a period of 2 years with the possibility of an extension for an additional year. The candidate is expected to do research at the interface of Algebra, Conformal Field Theory and String Theory.
Applicants must have a PhD in Theoretical Physics or Mathematics.
See the full announcement.
Further links:
Prof. Ch. Schweigert’s homepage
Some entries discussing the group’s work:
Unoriented Strings and Gerbe Holonomy
December 4, 2006
What Does the Classifying Space of a 2-Category Classify?
Posted by Urs Schreiber
My personal spy has just returned from the Nordic Conference in Topology that took place last week.
I hear that Tore A. Kro has new notes on his work with N. Baas and M. Bökstedt available online
N. Baas, M. Bökstedt, T. A. Kro
2-categorical K-theories.
They try to answer the question: What does the classifying space of a 2-category classify? Their answer is: for sufficiently well behaved topological 2-categories , the nerve of is the classifying space for charted -bundles.
Here a charted -bundle is essentially like what one would call the transition data for a 2-groupoid bundle #. The only difference is that no invertibility in is assumed. As a consequence, transition functions may go from patch to patch , but not the other way around.
The main application of this theory in these notes is a proof of the previously announced claim, that for the 2-category of Kapranov-Voevodsky 2-vector spaces the classifying space is the 2K-theory introduced by Baas, Dundas and Rognes. For the 2-category of Baez-Crans 2-vector spaces the classifying space is two copies of ordinary K-theory.
December 1, 2006
Klein 2-Geometry VIII
Posted by David Corfield
As John said:
categorification is a very broad project, like a huge tidal wave hitting the whole length of the shoreline. If certain parts don’t advance as fast as others, it’s really no big deal.
We’ve been trying to ride other parts of the wave of late, so there’s not much to report on last month’s events.
Something we did find is that the Poincaré 2-group is a full sub-2-group of the general linear 2-group of a skeletal Baez-Crans real 2-vector space of dimension (4, 1), i.e., with worth of objects and worth of morphisms from an object to itself.
There was also some speculation about the possibility and/or value of a composition of 2-groups, which prompted some exposition on -enriched profunctors.
Classical vs Quantum Computation (Week 8)
Posted by John Baez
Here are the last of the Fall quarter notes on Classical versus Quantum Computation:
- Week 8 (Nov. 30) - The Fixed Point Theorem and the diagonal argument (after Tom Payne). Cantor’s ‘negative’ use of diagonalization to prove that infinite bit strings cannot be enumerated, versus Curry’s ‘positive’ use of diagonalization to get a fixed point for any lambda-term in the untyped lambda calculus. Preview of coming attractions: quantum computation, and categorifying everything so far to see computation as a process.
Last week’s notes are here; next week’s notes are here.
Quantization and Cohomology (Week 8)
Posted by John Baez
Here are this week’s notes on Quantization and Cohomology:
- Week 8 (Nov. 28) - From particles to membranes, continued. A coordinate-free definition of -velocity. The action for a charged point particle in general relativity, versus the action for a charged membrane. The electromagnetic field versus its -form generalization.
Last week’s notes are here; next week’s notes are here.
 Posts with this logo use
Posts with this logo use