Talks at "Higher Categories and their Applications"

December 5, 2006

Talks at “Higher Categories and their Applications”

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

In the context of the workshop Higher Categories and their Applications that takes place at the Fields Institute next January, I am invited to give two talks, one on categorical and 2-categorical aspects of 2-dimensional quantum field theory, the other on higher parallel transport.

In order to harmonize this with other talks being given, I was asked to indicate what I might and might not mention. For those interested, here is some discussion.

A preliminary schedule and some of the abstracts can now be found here.

$MathML-enabled post (click for more details).$

Parallel Transport in low Dimensions (pdf)

Abstract:

A vector bundle with connection can be conceived as a suitable parallel transport 1-functor from paths in base space to vector spaces.

We categorify this and discuss various examples of locally trivializable 2-transport, some of them relevant for the description of charged 2-particles in formal high energy physics.

We point out how certain kinds of surface transport really have to be conceived as 3-transport; and we discuss the Chern-Simons 3-transport.

On 2-dimensional QFT: from Arrows to Disks.

Abstract:

The quantization of the charged point particle relates two 1-functors into vector spaces: the parallel transport on target space is turned by quantization into propagation on parameter space.

We categorify this and discuss how the 2-dimensional quantum field theory describing the charged 2-particle relates two 2-functors with values in 2-vector spaces.

Our goal is to explain and illuminate this way aspects of the categorical description of rational conformal field theory by the FRS theorem; like the relation of boundary fields (living on “D-branes”) to internal modules and of bulk fields to internal bimodules.

Here is a gentle introduction to the idea of how the space of states of strings are sections of 2-bundles:

Quantum 2-States: Sections of 2-vector bundles

More information is assembled here:

$\;\;\;$ On 2-dimensional QFT: from Arrows to Disks

The theme underlying all this is the desire to understand parallel transport and propagation in quantum field theory on the same footing. The unifying concept is apparently that of transport $n$ -functors, as indicated in the following table:

The quantization step from the left to the right column of this table therefore amounts to a procedure that sends parallel transport $n$ -functors to propagation $n$ -functors.

Posted at December 5, 2006 5:25 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1065

33 Comments & 25 Trackbacks

Read the post Local Transition of Transport, Anafunctors and Descent of n-Functors
Weblog: The n-Category Café
Excerpt: Conceps and examples of what would be called transition data or descent data for n-functors.
Tracked: December 8, 2006 7:21 AM

Read the post Communicating Thoughts on the Web
Weblog: The n-Category Café
Excerpt: Thinking, communicating and having math on the web.
Tracked: December 13, 2006 12:46 PM

Read the post Frobenius Algebroids with invertible Products
Weblog: The n-Category Café
Excerpt: Thinking of algebroids with invertible products as Frobenius algebroids.
Tracked: December 15, 2006 12:02 PM

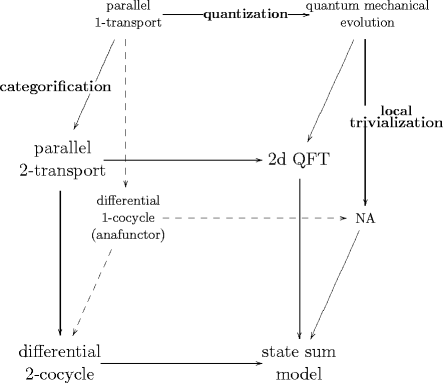
Parallel Transport in Low Dimensions

$MathML-enabled post (click for more details).$

I am working on a script for the talk on parallel transport. I am not satisfied with the result yet, but here are some tentative notes:

Parallel Transport in Low Dimensions

Posted by: urs on December 19, 2006 12:31 PM | Permalink | Reply to this

Helter Skelter: Categorification, Quantization and Local Trivialization

$MathML-enabled post (click for more details).$

Start in the top left corner, with a functor

(1)

\mathrm{tra} : P_1(X) \to \mathrm{Vect}

that takes paths in $X$ to morphisms of vector spaces.

Choose a cover of $X$ and trivialize the transport over each patch, inserting transition functions in the overlap. Move down the diagram to find a differential 1-cocycle, also known as an anafunctor #.

Now categorify. Move to the front of the diagram and find a differential 2-cocycle.

Regard this as describing the background field for a charged 2-particle. Suppose you know how to quantize this 2-particle and move to the right to find the 2-dimensional quantum field theory on the world sheet of the 2-particle.

when I get to the bottom I get back to the top of the slide, where I stop and I turn and I go for a ride…

All right, let’s do that again.

Back to the top: a connection on a bundle encoded in a 1-functor with values in vector spaces.

Now categorify: move to the front to obtain a 2-functor with values in 2-vector spaces.

Going downwards now would get us to the locally trivialized 2-functor with its transitions forming a differential 2-cocycle that we already know.

So let’s turn right. We find 2-dimensional quantum field theory in the Stolz-Teichner refinement of Segal’s global functorial notion of QFT.

Regarding this as a 2-vector transport as we did on the left and locally trivializing as before gets us to the 2-dimensional state sum models.

… and I see you again.

Start again in the top left, with a functor

(2)

\mathrm{tra} : P_1(X) \to \mathrm{Vect}

that takes paths in $X$ to morphisms of vector spaces.

Consider this as describing a charged particle and find the quantum theory of that particle: you move to the right and find a functor

(3)

U : 1\mathrm{Cob}_\mathrm{Riem} \to \mathrm{Vect}

describing the time evolution of the quantized charged particle.

Now do something that you rarely find discussed in your QM text books:

Take the particle to have spin and compute its partition function with antiperiodic boundary conditions. This amounts to locally trivializing the time evolution along the circle and inserting a transition function with value $-1$ : we arrive at NA (no established term for this).

If you figure out what’s really going on here, categorification takes you to the front, and once again to the 2-dimensional state sum model.

Posted by: urs on December 19, 2006 5:35 PM | Permalink | Reply to this

Re: Helter Skelter: Categorification, Quantization and Local Trivialization

Is your quantization arrow to be seen as an instance of something much larger? I mean should we be looking at quantization as a functor from a classical category to a quantum category, as Landsman suggests? Maybe for your purposes of categorification, it’s best to start with a single system.

Posted by: David Corfield on January 4, 2007 10:07 AM | Permalink | Reply to this

Re: Helter Skelter: Categorification, Quantization and Local Trivialization

$MathML-enabled post (click for more details).$

Is your quantization arrow to be seen as an instance of something much larger? I mean should we be looking at quantization as a functor from a classical category to a quantum category, as Landsman suggests? Maybe for your purposes of categorification, it’s best to start with a single system.

Thank you for this question.

I should make the following remarks concerning the statement of that cube above:

At the moment, this cube is heuristic. I don’t claim that I have a good general-purpose definition of all the vertices and all the arrows such that there would be a theorem that this cube commutes.

But I think it should.

At the moment, this cube serves for me the purpose of a 3-dimensional map. A map that needs to be refined.

That’s the first comment.

The second comment is that I restrict attention to the quantization of classical systems of a very special kind:

instead of considering what it might mean to have a quantization prescription applicable to every Poisson manifold, as Landsman does, I only consider classical systems of the form

“a charged $n$ -particle coupled to an $n$ -vector bundle”.

John urged me not to say “charged $n$ -particle”, because it will confuse everybody. But some concise terminology for the following natural idea deserves to exist (I am open for suggestions):

If we disregard the kinetic contribution for a moment (which may be thought of as arising universally on general grounds #) then the classical action of a charged particle (like the electron, charged under the electgromagnetic field, or a quark, charged under the nuclear “color gauge field”) is entirely encoded in a vector bundle with connnection $\nabla$ – or, equivalently, a parallel transport functor $\mathrm{tra}_\nabla$ .

An analogous statement is true for the “charged string”. Apart from the kinetic contribution, the action is entirely encoded in a line bundle gerbe with connection – or, equivalently, a parallel transport 2-functor.

Applying either path integral quantization (using the generalized Feynman-Kac formula), or geometric quantization to the charged particle leads to the result that the quantum theory associated to the parallel transport functor $\mathrm{tra}_\nabla$ is the functor

(1)

t \mapsto U_\nabla(t) = \exp(i t \nabla^\dagger \circ \nabla) \,.

An analogoues statement applies to the charged string.

So this is my point here: if we restrict attention to those classical systems that describe ( $n-1$ )-dimensional objects whose classical phases are given by parallel transport in an $n$ -bundle with connection, then quantization seems to be a procedure that sends parallel transport $n$ -functors to time evolution $n$ -functors

(2)

\mathrm{tra}_\nabla \mapsto U_\nabla \,.

This proceudre involves, on the level of objects, passing from an $n$ -vector bundle to its $n$ -vector space of sections. On the level of morphisms it amounts to forming from a parallel transport $n$ -functor the corresponding covariant derivative.

Both are very natural operations on a transport functor.

I imagine that, when worked out properly, this assignment may be suitably understood as a morphism between $n$ -categories of $n$ -functors.

But this requires more thinking on my part.

Posted by: urs on January 4, 2007 1:04 PM | Permalink | Reply to this

Re: Helter Skelter: Categorification, Quantization and Local Trivialization

$MathML-enabled post (click for more details).$

Urs wrote:

John urged me not to say “charged n-particle”, because it will confuse everybody.

Not everybody — just your audience at the Fields Institute. Mathematical physicists will instantly understand that ‘charge’ means ‘representation of a Lie group $G$ ’, so that the wavefunction of a charged particle is not an element of $L^2(X)$ but of $L^2(X,E)$ , where $X$ is the configuration space and $E$ is a vector bundle associated to some principal $G$ -bundle over $X$ . So, they’ll be ready to categorify this idea — at least if they’re ready to categorify anything. But, your audience at the Fields Institute will consist largely of experts on homotopy theory and n-categories. Many of these people last met ‘charge’ back in their high school or college electromagnetism course. Using this term will merely confuse them — since you don’t have time for a quick review of how electromagnetism generalizes to Yang–Mills theory, etcetera etcetera.

For these people, the big revelation will be that categorifying the physics of particles gives the physics of strings, and categorifying that gives the physics of 2-branes, and so on. They won’t know string theory, but they’ll have heard of it — and since they like $n$ -categories, they’ll be very excited to hear that maybe string theory will make more sense using n-categories. Mathematicians are always hoping that their branch of math will be relevant to physics, or at least help them understand what physicists are doing… though few of them take the time to seriously study what physicists are doing.

So: saying “n-particle = (n-1)-brane” is a great idea, as long as you also tell them a 1-brane is a string and a 0-brane is a normal particle. But bringing the term ‘charge’ into the game is too much for a 1-hour talk (knowing all the other stuff you intend to cover).

General philosophy: when giving a talk, one needs to carefully ponder the audience and what they know. This is easy for the Fields conference, since you can see a list of the speakers and a list of other participants. You’ll note the absence of mathematical physicists except you and me! Knowing the audience, one can choose ones terminology. So, the ‘same’ talk to different audiences will come out sounding very different.

Posted by: John Baez on January 4, 2007 5:29 PM | Permalink | Reply to this

terminology

$MathML-enabled post (click for more details).$

So: saying “ $n$ -particle = $(n-1)$ -brane” is a great idea, as long as you also tell them a 1-brane is a string and a 0-brane is a normal particle.

Okay good. I will do that.

(I am hoping that it will not sound like I have any intentions at all to argue about this when I cannot refrain from remarking that $n$ -particle is a term supposed to be essentially self-explanatory to $n$ -category theorists: a 1-particle must be a plain particle, by common convention. A 2-particle must be some kind of categorification thereof. And it evades the problem of why the “strings” I talk about might, but need not, be exactly those (“fundamental”) strings they talk about in string theory.)

But bringing the term ‘charge’ into the game is too much for a 1-hour talk.

Okay, good. I won’t mention it then.

My intention was to define what the term “charged particle” means by saying: “I consider smooth functors with values in $\mathrm{Vect}$ . Physicists happen to call this a ‘charged particle’.”.

$\;\;\;$ (knowing all the other stuff you intend to cover)

I have drastically reduced the intentions in that now

A) everything about associated $n$ -bundles I have moved from first to second talk

B) after explaining what a categorified line bundle is, the second talk only explains what a section of such a beast is, closing with the remark that this is one way to understand D-branes.

Posted by: urs on January 4, 2007 7:31 PM | Permalink | Reply to this

Re: Talks at “Higher Categories and their Applications”

$MathML-enabled post (click for more details).$

I would like to “explain and illuminate aspects of the categorical description of rational conformal field theory by the FFRS theorem” by showing how the ingredients of that theorem can be understood as coming from a locally trivialized 2-vector transport.

But merely stating the FFRS theorem # takes its time. In rough outline, it achieves the following:

I thought that instead of trying to explain what all this means in detail, I’d just exhibit what this prescription does to $X$ the disk with a bulk and a boundary insertion.

Posted by: urs on December 20, 2006 4:35 PM | Permalink | Reply to this

Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Quantum 2-States: Sections of 2-vector bundles

Abstract:

Quantization of point particles is a process that sends a vector bundle to its space of sections (“states”); and a connection on the vector bundle to an action on this space of states.

This situation can be categorified. Suitable sections of line-2-bundles ( $\simeq$ line bundle gerbes) describe states of open strings.

Over the endpoints of the string, such a 2-section amounts to a choice of gerbe module. This is known as a “D-brane”.

Posted by: urs on January 3, 2007 1:10 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Probably a worthless thought, but might something be gained by expressing the classical part of the story in such a way that it looks more like the quantum? This follows on from what we were talking about here concerning change of rigs. Litvnov suggests that:

in parallel with the traditional mathematics over fields, its “shadow,” the idempotent mathematics, appears. This “shadow” stands approximately in the same relation to the traditional mathematics as does classical physics to quantum theory. (p. 2)

But more specifically,

Basic equations of quantum theory are linear; this is the superposition principle in quantum mechanics. The Hamilton–Jacobi equation, the basic equation of classical mechanics, is nonlinear in the conventional sense. However, it is linear over the semirings $R_{max}$ and $R_{min}$ . (p. 8)

Hmm, couldn’t one develop bundle theory for $R_{max}$ ? It has modules defined over it.

At a conference organised by Litvanov, I see Mascari talked about ‘Higher Dimensional Idempotent Mathematics: Idempotent Mathematics and Higher Dimensional Algebra’.

Posted by: David Corfield on January 3, 2007 2:33 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Probably a worthless thought […]

Not at all! A very worthwhile remark. It is great that you keep pushing me in this direction. I ought to better understand this.

but might something be gained by expressing the classical part of the story in such a way that it looks more like the quantum?

If we can keep the functorial picture of quantum mechanics and understand the classical limit entirely in terms of deformations of the ground field, I’d be very happy.

Litvinov suggests […]

I’ll take a closer look at that.

At a conference organised by Litvinov […]

On page 15 of these proceedings I find the statement

The Hamilton-Jacobi equation is an idempotent version of the Schrödinger equation.

That’s very nice. This aspect of the matter is much close to the techniques that I have under good control than the path integral picture (Fourier $\leftrightarrow$ Legendre) is, when it comes to categorification.

I can roughly see how the above statement is true. But could you point me directly to some page in some paper where this particular statement is discussed in detail? Thanks.

Hmm, couldn’t one develop bundle theory for $R_\mathrm{max}$ ?

Yes, certainly. That’s why I keep on going in these discussions about formulating everything “arrow theoretically” (of course after having been taught to do so by Baez/Bartels). If we have a good idea what the arrow theory of, say, quantum mechanics is, we can rather straightforwardly interpret it in all kinds of new contexts.

Okay, so as a warmup we should think about this

Exercise: Characterize suitably well-behaved functors that send paths in a space $X$ to morphisms of $\mathbb{R}_\mathrm{max}$ -modules

(1)

\mathrm{tra} : P_1(X) \to {}_{\mathbb{R}_\mathrm{max}}\mathrm{Mod} \,.

It should help to start with the trivial $\mathbb{R}_\mathrm{max}$ -bundle with connection, given by a functor of the above sort that sends every point of $X$ to $\mathbb{R}_\mathrm{max}$ , regarded as a module over itself:

(2)

\mathrm{tra}(x) = \mathbb{R}_\mathrm{max} \,.

A morphism of $\mathbb{R}_\mathrm{max}$ -modules

(3)

\mathbb{R}_\mathrm{max} \to \mathbb{R}_\mathrm{max}

should simply be multiplication by an element in $\mathbb{R}_\mathrm{max}$ .

So we can equivalently think of these morphisms as morphisms of the abelian group

(4)

G = (\mathbb{R},+) \,,

I guess.

We can identify this group with its Lie algebra by declaring that

(5)

1 = \exp(1) \,,

where on the left 1 denotes a group element and on the right we have the exponential map applied to “1” regarded as an element of the Lie algebra.

Then

(6)

\exp(1)\exp(1) = 1 + 1 = 2 = \exp(2)

and so on.

Anyway, this should mean that connection on a trivial $\mathbb{R}_\mathrm{max}-\mathrm{Mod}$ -bundle is nothing but a connection on a trivial real line bundle.

Aha, okay. So the peculiarities of idempotent mathematics come in only as we sum over several paths. Namely we get

(7)

\sum_{(x \stackrel{\gamma}{\to} y)} \mathrm{tra}(\gamma) = \mathrm{max}_\gamma \mathrm{tra}(\gamma) \,.

So this path integral picks out the contribution of that path from $x$ to $y$ with the “largest parallel transport displacement”.

Right, this is how the classical limit of quantum mechanics has a chance of being expressed in terms of idempotent rings.

Hm, maybe what I’d need to understand next is the “Schrödinger equation” version of this:

what would be the covariant derivative $\nabla$ associated with the parallel transport $\mathrm{tra}$ in the world of idempotent rings?

Hm…

Posted by: urs on January 3, 2007 3:28 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

Litvinov discusses the idea that the Hamilton-Jacobi equation is an idempotent version of the Schrödinger equation in section 6 of this. On p. 10 he gives references for a rigorous treatment rather than his own heuristic one.

Posted by: David Corfield on January 3, 2007 3:57 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Litvinov discusses the idea that the Hamilton-Jacobi equation is an idempotent version of the Schrödinger equation in section 6 of this.

Thanks. I have read that now.

I am not sure yet that I do see the full abstract picture.

What Litvinon describes is pretty much exactly what one finds in physics textbooks when it says “now we let $\hbar$ tend to 0”.

That’s all fine, but I was hoping that the idempotent math picture would offer us a more abstract description of this process, more amenable to categorification.

For instance, the above procedure rests entirely on the fact that we can assume we know that a state of a quantum system is a complex function on configuration space.

Even for ordinary quantum mechanics this is an oversimplification. In general that state will be a section of some line bundle. But okay, locally it looks like a complex function.

But now when I categorify, a state will no longer be a section of a line bundle, but of a line-2-bundle, as I describe in the above notes.

Again, I’d be content with assuming for the moment that this line-2-bundle is trivial. But even then it is not really obvious what “sending $\hbar$ to 0” would mean here.

As I describe above, a state of an open “2-particle” (string) coupled to a line-2-bundle is a collection consisting of two twisted vector bundles (the “D-branes” at the endpoints of the string) and a certain morphism between them.

What would it mean to take the classical limit of that?

I am hoping that “taking the classical limit” can be expressed entirely in terms of deformation of the $n$ -ring we are working over.

For instance, the above 2-states of the open string are elements of a module category which is acted on by the 2-ring (= abelian monoidal category) of vector bundles that are equivariant with respect to translation along the support of the D-branes.

I imagine that it should be possible to consider a 1-parameter deformation of this 2-ring

(1)

\mathrm{VectBund}(X/\mathrm{branes}) \to \mathrm{something}

which we may interpret as a categorification of the deformation

(2)

\mathbb{R} \to \mathbb{R}_\mathrm{max} \,.

Then, somehow, it should be possible to subject this entire setup, with 2-states living in $\mathrm{VectBund}(X/\mathrm{branes})$ -module categories, to this deformation.

I am not sure yet how that would work. It would be easier to understand if I had a similarly “abstract” or “arrow theoretic” idea of the classical limit for ordinary quantum mechanics.

Posted by: urs on January 3, 2007 4:29 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

What Litvinov describes is pretty much exactly what one finds in physics textbooks when it says “now we let $\hbar$ tend to 0”.

So although he claims to be doing something instead of taking the semiclassical limit (top of p. 10), you don’t think this amounts to much of a difference?

I have a vague recollection of Michael Berry talking to a philosophy conference about the intricacies of taking semiclassical limits. Ah, this paper, “Chaos and the Semiclassical Limit of Quantum Mechanics (Is the Moon There When Somebody Looks?)” seems to be the one. Available here.

So what’s the point? That we should expect the taking of semiclassical limits to be complicated affairs, and so probably not amenable to neat arrow theoretic formulations involving rig replacement? So you’re unlikely to get

a similarly “abstract” or “arrow theoretic” idea of the classical limit for ordinary quantum mechanics.

Then again maybe there’s no reason that rig replacement could not produce complicated behaviour.

What’s the difference between ‘classical’ and ‘semiclassical’?

Posted by: David Corfield on January 4, 2007 9:31 AM | Permalink | Reply to this

semiclassical

$MathML-enabled post (click for more details).$

What’s the difference between ‘classical’ and ‘semiclassical’?

“Semiclassical “usually refers to an expansion about the classical limit.

If you like, instead of assuming that $\hbar = 0$ you assume that $\hbar^n = 0$ , for some $n \in \mathbb{N}$ .

A standard semiclassical technique is saddle point expansion. Instead of just considering the saddle point of the path integral, one approximates it by a Gaussian (i.e. take “ $\hbar^3 = 0$ ”).

Posted by: urs on January 4, 2007 1:11 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

So although he claims to be doing something instead of taking the semiclassical limit (top of p. 10), you don’t think this amounts to much of a difference?

He first recalls that in physics textbooks one writes the wave function as $\psi = a e^{iS/\hbar}$ , plugs it into the Schrödinger equation and then takes $\hbar \to 0$ .

Then he announces to follow a different route, as you note. But look at what he does:

he first renames $\hbar$ as $\hbar = -i h$ , then he renames $\psi$ as $u$ and also renames $S$ such as to absorb the $a$ from before.

So now

(1)

\psi = u = \exp(S/h)

just by renaming. He plugs that into Schrödinger’s equation and sends $\h \to 0$ .

It’s exactly the same procedure as in the physics textbooks.

Please note well: I am not saying there is anything objectionable about this at all. It’s good.

The interesting new observation - which does go beyond what one finds in ordinary physics textbooks - is that it may be useful to regard that very procedure as defining a deformation of the ring of real numbers to an idempotent ring.

That’s good. It often happens that physicsist work with something without identifying the natural structures implicit in their work. Then a mathematician comes along, points at various pages of various physics text and calls various concepts by their abstract mathematical names.

In the optimal case, this identification of structures allows us to subsequently generalize and improve our understanding of the original situation.

That’s what I was hoping whould happen here. Probably it does. But I do not see it yet.

For instance: consider a Poisson manfiold and do geometric quantization with it to obtain an associated quantum theory: a line bundle, a space of sections, etc.

Can we use the passage from $\mathbb{R}_+$ to $\mathbb{R}_\mathrm{max}$ to systematically say what the dequantization of this system is?

Posted by: urs on January 4, 2007 4:59 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

Is there an inequality of treatment between point and path going on when one compares classical and quantum? I mean the quantum propagator ends up being formed over an average of paths averaged over possible start and end points. In the classical case one tends to imagine the start and end point as given and then note that the path traversed is extremal, so an integral in the idempotent sense. But why not see the start and end points as also selected by an integration/extremisation?

Posted by: David Corfield on January 4, 2007 5:42 PM | Permalink | Reply to this

Paths and Points

$MathML-enabled post (click for more details).$

I mean the quantum propagator ends up being formed over an average of paths averaged over possible start and end points.

That’s not quite the way I would put it.

The “amplitude” for a passage from a fixed point $x$ to a fixed point $y$ is given by an integral of the exponentiated action over all paths going between $x$ and $y$ .

So we get one amplitude per pair of points, hence a “matrix” - or rather a linear operator.

But why not see the start and end points as also selected by an integration/extremisation?

This is the point of view promoted by Dan Freed, originally:

above # I stated a dichotomy between the “kinematical” and the “dynamical” aspect of quantization.

We do one thing to paths: namely we integrate the action over them.

We seem to do another thing to points: namely we form the space of sections of the vector bundle fibers living over them.

Dan Freed noticed that, when suitably looked at, this latter step should also be a kind of integration. Or, conversely, that the former step should also a way of taking sections.

This aims at unifying the treatment of points and paths - and then of paths of paths, etc.

Aspects of more precise formulations of this idea appear in some modern treatments of topological field theories, as for instance indicated in this description of Chern-Simons theory.

The slogan is, roughly: quantization is push forward to a point.

See for instance p. 3 of this for how one may think of the path integral as a pushforward to a point.

Analogously, forming the space of sections of a vector bundle can be understood as push-forward of the vector bundle to a point (“in K-theory”).

If Bruce Bartlett weren’t on vacation, he would probably help us out with some related remarks.

Posted by: urs on January 4, 2007 6:26 PM | Permalink | Reply to this

Re: Paths and Points

$MathML-enabled post (click for more details).$

quantization is push forward to a point

So from the perspective of the infamous charged particle the big question is:

what does it mean to push a parallel transport functor forward to a “point”??

There must be a very elegant mechanism at work, but I don’t fully see it yet.

But it all looks quite suggestive:

say we have a charged particle on a space $X$ . With $P_1(X)$ a category of paths in $X$ , its nature is determined by a suitable functor

(1)

\mathrm{tra} : P_1(X) \to \mathrm{Vect} \,.

Quantization, we know, is a process which turns this functor on all paths into a functor on a single abstract path called the worldline or parameter space.

We can model parameter space for instance by a category with just two objects and a single nontrivial morphism between them

(2)

\{a \to b\} \,.

The “space” of all paths in $X$ is

(3)

[\{a\to b\}, P_1(X)] \,.

Somehow quantization amounts to pulling back $\mathrm{tra}$ to this space of all paths and then “pushing it forward” to a functor on $\{a \to b\}$ alone, namely

(4)

U : (a \to b) \mapsto H_a \stackrel{\exp(i \Delta)}{\to} H_b \,,

where $H$ is the space of sections of the original bundle and $\exp(i \Delta)$ the propagator obtained from the path integral (integral over $[\{a\to b\}, P_1(X)]$ , in a sense).

I was trying to identify the abstract nonsense of this “pushforward to a single abstract path” here and here.

I still don’t fully understand it, though.

I am hoping that in the end it is true that “quantization of the charged particle” is some sort of colimit, roughly like an expression

(5)

\int_{[\{a\to b\},P_1(X)]} \mathrm{tra}_*

or so, and that all the subtleties, like the well-definedness of the path integral etc, can the be understood as related to the question in which contexts this colimit actually exists.

Does that hope make sense to anyone?

Posted by: urs on January 5, 2007 12:22 PM | Permalink | Reply to this

Re: Paths and Points

Vacation has just finished… time to prepare for a hectic Fields workshop!

Posted by: Bruce Bartlett on January 5, 2007 1:28 PM | Permalink | Reply to this

Bruce is back

$MathML-enabled post (click for more details).$

Vacation has just finished…

Hi Bruce!

Hope you had a good vacation.

Are we going to see you at Café Diplomatico?

By the way, in case you missed it:

while you were away you were kindly asked if you could provide comments on Toby’s thesis.

Posted by: urs on January 5, 2007 1:42 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

David wrote:

Is there an inequality of treatment between point and path going on when one compares classical and quantum?

Nope.

I mean the quantum propagator ends up being formed over an average of paths averaged over possible start and end points.

No, the quantum propagator for a particle going from a point $p$ in spacetime to a point $q$ in spacetime is the integral of $exp(iS/\hbar)$ over all paths from $p$ to $q$ .

In the classical case we don’t talk about a ‘propagator’ — we speak instead of ‘Hamilton’s principal function’. The Hamilton’s principal function for a particle going from $p$ to $q$ is the infimum of $S$ over all paths from $p$ to $q$ .

So: when we go from quantum to classical, minimization replaces addition, and we work with $S$ instead of $exp(iS/\hbar)$ .

The fun part is seeing how the quantum case reduces to the classical case in the $\hbar \to 0$ limit.

I explained this stuff here, with one slight difference: I made things simpler, by comparing classical mechanics to statistical mechanics instead of quantum mechanics!

So, instead of using the words ‘action’, ‘Planck’s constant’ and ‘ $exp(iS/\hbar)$ ’, I used the words ‘energy’, ‘temperature’ and ‘ $exp(-E/T)$ ’. Apart from that, the whole story was almost the same — but simpler, because no complex numbers enter the game! Instead of complex amplitudes, we just have nonnegative real ‘relative probabilities’.

So, to see how statistical mechanics reduces to classical mechanics in the $T \to 0$ limit, all we need to think about is the temperature-dependent rig $\mathbb{R}^T$ , which is isomorphic to the rig of nonnegative real numbers for all positive temperatures, but reduces to the idempotent rig $\mathbb{R}^{min}$ as $T \to 0$ . I already defined all these rigs back then, so I won’t do it here.

To go from statistical mechanics to quantum mechanics, we then need to do just one more thing: replace the rig of nonnegative real numbers (relative probabilities) by the rig of complex numbers (amplitudes).

Posted by: John Baez on January 5, 2007 12:02 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

the quantum propagator for a particle going from a point $p$ in spacetime to a point $q$ …

Yes, but don’t you apply it to states which aren’t position eigenvectors? So there’s a superposition of positions and then a sum over paths between positions, whereas in the classical case there’s one pair of positions and one path.

To go from statistical mechanics to quantum mechanics, we then need to do just one more thing: replace the rig of nonnegative real numbers (relative probabilities) by the rig of complex numbers (amplitudes).

I guess what Urs and I are wondering is what to make of this fact. Having lectured statistical mechanics to our students, do we say to them “don’t bother going now to the quantum mechanics lecture, you can just change the rig in what I told you.”?

How systematic is this rig changing business? Might it be quite subtle, as when you pass to the $q = 0$ version of $q$ -mathematics. Here we are chatting about that back in 2003. Did you ever find out more about crystal bases?

I’m also wondering what to make of the ‘insight’ that homotopy theory is a kind of (generalized) truth-value valued mechanics, as we once noted. Urs has mentioned the idea of the space of sections as an integral along a path, but we were thinking of the path itself as an integral. At least, its existence was registered by a integral of truth values, and the thought was raised of the path itself as an integral of its points.

Is this insight not related to the fact that the topology of a space and the physics possible within a space constrain each other?

Posted by: David Corfield on January 5, 2007 11:52 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

David wrote:

John almost wrote:

the quantum propagator for a particle going from a point $p = (t,x)$ in spacetime to a point $p' = (t',x')$ …

Yes, but don’t you apply it to states which aren’t position eigenvectors?

You can if you want.

So there’s a superposition of positions and then a sum over paths between positions, whereas in the classical case there’s one pair of positions and one path.

Okay, so you’re telling me this:

In the quantum case, the set of states is a module for the rig $\mathbb{C}$ : we can add states and multiply them by complex numbers. Ignoring crucial details of analysis, as physicists always do, we may say the position eigenstates form a ‘basis’ of states. So, knowing the propagator $G(t,x;t',x')$ , which gives the amplitude for a position eigenstate at time $t$ to evolve to a position eigenstate at time $t'$ , we can compute the amplitude for any state at time $t$ to evolve to any state at time $t'$ .

By contrast, in the classical case, the set of states is not a module of the rig $\mathbb{R}^{min}$ .

But is this really true? Maybe there is some meaning to $\mathbb{R}^{min}$ -linear combinations of ‘position eigenstates’ in the classical case! But, perhaps they’re ‘degenerate’ in some drastic way, since addition in $\mathbb{R}^{min}$ is idempotent.

As some evidence that this idea is not utterly insane: the superposition principle does work in the case of statistical mechanics, where we use the rig $\mathbb{R}^T$ . Here our superpositions are just the usual probabilistic sort of ‘mixtures’ of probability distributions.

And, as $T \to 0$ , $\mathbb{R}^T \to \mathbb{R}^{min}$ — statistical mechanics reduces to classical mechanics at absolute zero, when the ‘thermal noise’ goes away. So, maybe there should be a kind of superposition principle in classical mechanics, the $T \to 0$ limit of the superposition principle in statistical mechanics!

But, right now I think it must be ‘degenerate’ in some way.

David wrote:

John wrote:

To go from statistical mechanics to quantum mechanics, we then need to do just one more thing: replace the rig of nonnegative real numbers (relative probabilities) by the rig of complex numbers (amplitudes).

I guess what Urs and I are wondering is what to make of this fact. Having lectured statistical mechanics to our students, do we say to them “don’t bother going now to the quantum mechanics lecture, you can just change the rig in what I told you.”?

Obviously we don’t do that — even though we could. Instead, we first teach them quantum mechanics, and later we say something like this:

There’s a deep, mysterious relation between quantum mechanics and statistical mechanics, called ‘Wick rotation’, which consists of replacing time by imaginary time. This lets us apply all the techniques of statistical mechanics to quantum mechanics. It’s especially useful in quantum field theory — especially for understanding concepts like ‘renormalization’, ‘phase transitions’, ‘critical points’, ‘spontaneous symmetry breaking’, and so on. Indeed, if you look at a book on rigorous quantum field theory like Quantum Physics: A Functional Integral Point of View by Glimm and Jaffe, you’ll see that right near the start they do Wick rotation, and from then on they study quantum fields using ideas from statistical mechanics!

There’s a lot more to think about in what you said, but I’ve got to run…

Posted by: John Baez on January 6, 2007 12:49 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

By contrast, in the classical case, the set of states is not a module of the rig $\mathbb{R}^\mathrm{min}$ .

This might be a matter of choosing the right canonical coordinates. Litvinov’s discussion shows that in terms of action variables the states do form a module of this sort. I think.

Posted by: urs on January 7, 2007 5:29 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

So, maybe there should be a kind of superposition principle in classical mechanics

Phew! That’s exactly what I’ve been driving at, not very coherently.

Posted by: David Corfield on January 6, 2007 12:53 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

David wrote:

Phew! That’s exactly what I’ve been driving at, not very coherently.

Sorry, it took me a while to get your secret point: if different forms of mechanics are all just matrix mechanics over different rigs, where’s the superposition principle in classical mechanics?

Right now I feel the best way to tackle this puzzle is by studying classical statics instead of classical mechanics. Classical statics is the chilly $T \to 0$ limit of statistical mechanics at temperature $T$ . It’s still statistical mechanics, so all the stuff about probability theory should still apply. So, it should still have a superposition principle: superposition of probabilities. But, it’s deterministic — at absolute zero, a classical system in equilibrium will sit at its least-energy state with probability 1. So, using probability theory will feel like ‘overkill’!

Then, we can Wick-rotate to go from classical statics to classical mechanics. I neglected to mention this point in my previous post! We really have four cases to keep in mind here:

classical statics         classical mechanics
statistical mechanics     quantum mechanics

But, the term ‘statistical mechanics’ is misleading, just like ‘thermodynamics’ - because these subjects are really about statics at nonzero temperature! Different terminology might make the four cases clearer:

classical statics         classical dynamics
thermal statics           quantum dynamics

The two columns in the chart are related by the change of variables

$T = i \hbar.$

The top row in the chart is the $T \to 0$ or $\hbar \to 0$ limit of the more general bottom row.

You want to understand the superposition principle in classical dynamics. If it exists, it should arise as a limit of the superposition principle in quantum dynamics. But, I’m finding it easier to imagine how some superposition principle in classical statics arises as a limit of the superposition principle in thermal statics.

I’m still confused about a lot of stuff, though. We really should systematically work out the same problem in all four corners of the chart. Maybe the problem of the hanging spring/thrown rock.

But alas, I have to get up at 3:30 am tomorrow to catch a plane to Toronto, so now is not the best time for me to work this out.

Posted by: John Baez on January 6, 2007 1:33 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Let me just jot down a few random thoughts I had while awake in the night.

1) $\mathbb{R}$ has Euler characteristic $-1$ so $\mathbb{R}_{min}$ has Euler characteristic $0$ .

2) $\mathbb{R}_{min}$ , not being a field, can have more interesting modules than $\mathbb{C}$ . E.g., the rig of truth values is a module (maybe able to represent the presence of a particle).

3) Is there some relation between Wick rotation and the Fourier transform? I seem to recall one of the QG seminars spending time on the Fourier transform as a quarter turn.

Posted by: David Corfield on January 6, 2007 11:55 AM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

If $\mathbb{R}^T$ is the rig for thermal statics (statistical mechanics), and Wick rotation sends $T$ to $i \hbar$ , then what is $\mathbb{R}^{i \hbar}$ , and what does it converge to as $\hbar \to 0$ ?

Posted by: David Corfield on January 6, 2007 3:57 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

You want to understand the superposition principle in classical dynamics. If it exists, it should arise as a limit of the superposition principle in quantum dynamics. But, I’m finding it easier to imagine how some superposition principle in classical statics arises as a limit of the superposition principle in thermal statics.

This is, by the way, pretty much the point that Litvinov makes in his discussion around p. 6. There he notes that deriving the Hamilton-Jacobi equation from Schrödinger’s equation by the usual $\hbar \to 0$ in particular tells us that the Hamilton-Jacobi equation is linear over $\mathbb{R}_\mathrm{max}$ .

Posted by: urs on January 7, 2007 5:21 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

There’s a whole website devoted to Max-Plus algebra. If you follow up the ‘searcher’, Jean-Pierre Quadrat, you can read his Min-Plus Linearity and Statistical Mechanics, which on p. 6 discusses the Hamilton-Jacobi equation.

Another relevant paper is Roublev’s On Minimax and Idempotent Generalized Weak Solutions to the Hamilton-Jacobi Equation.

Posted by: David Corfield on January 10, 2007 8:02 PM | Permalink | Reply to this

Re: Sections of Line-2-Bundles and D-branes

$MathML-enabled post (click for more details).$

Where does quantum thermodynamics fit into your chart, if you’ve replaced the $T$ by $i \hbar$ ? I see that in the winter 2004 QG seminar you treated it in parallel with classical statistical mechanics. Is it that there’s a statistical mechanics for each complex number, the real part corresponding to temperature, the complex part the value of $\hbar$ ?

And then there’s my related confusion with Legendre and Laplace/Fourier transforms. Might one hope to find a use for a categorical Fourier transform in the context of your CTherm and QTherm?

Posted by: David Corfield on January 9, 2007 12:45 PM | Permalink | Reply to this

Read the post The first part of the story of quantizing by pushing to a point...
Weblog: The n-Category Café
Excerpt: Taking sections of transport functors by pushing them to a point.
Tracked: January 13, 2007 8:32 PM

Read the post Aaronson on the Nature of Quantum Mechanics
Weblog: The n-Category Café
Excerpt: Scott Aaronson on the nature of quantum mechanics.
Tracked: January 16, 2007 3:05 PM

Read the post D-Branes from Tin Cans, III: Homs of Homs
Weblog: The n-Category Café
Excerpt: Sections of sections, their pairing and n-disk correlators.
Tracked: January 19, 2007 9:10 AM

Read the post Cocycle Category
Weblog: The n-Category Café
Excerpt: Bruce Bartlett reports on Rick Jardine's concept of 'cocycle categories' and their relation to anafunctors.
Tracked: January 24, 2007 11:03 AM

Read the post The Globular Extended QFT of the Charged n-Particle: Definition
Weblog: The n-Category Café
Excerpt: Turning a classical parallel transport functor on target space into a quantum propagation functor on parameter space.
Tracked: January 24, 2007 8:15 PM

Read the post Globular Extended QFT of the Charged n-Particle: String on BG
Weblog: The n-Category Café
Excerpt: The string on the classifying space of a strict 2-group.
Tracked: January 26, 2007 3:02 PM

Read the post QFT of Charged n-particle: Chan-Paton Bundles
Weblog: The n-Category Café
Excerpt: Chan-Paton bundles from the pull-push quantization of the open 2-particle.
Tracked: February 7, 2007 8:23 PM

Read the post Isham on Arrow Fields
Weblog: The n-Category Café
Excerpt: On Chris Isham's notion of an "arrow field" on a category.
Tracked: February 8, 2007 7:24 PM

Read the post QFT of Charged n-Particle: Algebra of Observables
Weblog: The n-Category Café
Excerpt: The algebra of observables as certain endomorphisms of the n-category of sections.
Tracked: February 28, 2007 2:44 AM

Parallel Transport and Quantization

$MathML-enabled post (click for more details).$

I am currently at Karlstad University, visiting two Fs from FFRS.

Two days ago I gave a talk to a couple of physicists, which was roughly following these notes:

Parallel Transport and Quantization

Posted by: urs on February 28, 2007 1:24 PM | Permalink | Reply to this

Read the post QFT of Charged n-Particle: Disk Path Integral for String in trivial KR Field
Weblog: The n-Category Café
Excerpt: The arrow-theoretic perspective on the path integral for the disk diagram of the open string.
Tracked: March 5, 2007 10:21 PM

Read the post The First Edge of the Cube
Weblog: The n-Category Café
Excerpt: The notion of smooth local i-trivialization of transport n-functors for n=1.
Tracked: May 4, 2007 8:59 PM

Read the post Report from "Workshop on Higher Gauge Theory"
Weblog: The n-Category Café
Excerpt: Report-back on a little symposium titled "Higher Gauge Theory" (but concerned just with abelian gerbes) that took place at the AEI in Golm.
Tracked: May 9, 2007 11:54 AM

Read the post Extended Quantum Field Theory and Cohomology, I
Weblog: The n-Category Café
Excerpt: On understanding extended quantum field theory and generalized cohomology.
Tracked: June 8, 2007 2:26 PM

Read the post Extended QFT and Cohomology II: Sections, States, Twists and Holography
Weblog: The n-Category Café
Excerpt: How transformations of extended d-dimensional quantum field theories are related to (d-1)-dimensional quantum field theories. How this is known either as twisting or as, in fact, holography.
Tracked: June 10, 2007 7:56 PM

Read the post Arrow-Theoretic Differential Theory
Weblog: The n-Category Café
Excerpt: We propose and study a notion of a tangent (n+1)-bundle to an arbitrary n-category. Despite its simplicity, this notion turns out to be useful, as we shall indicate.
Tracked: July 31, 2007 7:07 PM

Read the post QFT of Charged n-Particle: Towards 2-Functorial CFT
Weblog: The n-Category Café
Excerpt: Towards a 2-functorial description of 2-dimensional conformal field theory. A project description.
Tracked: August 3, 2007 10:41 PM

Read the post That Shift in Dimension
Weblog: The n-Category Café
Excerpt: What makes the Kontsevich-Cattaneo-Felder theorem tick? How can it be that an n-dimensional quantum field theory is encoded in an (n+1)-dimensional one?
Tracked: August 25, 2007 9:50 AM

Read the post The Concept of a Space of States, and the Space of States of the Charged n-Particle
Weblog: The n-Category Café
Excerpt: On the notion of topos-theoretic quantum state objects, the proposed definition by Isham and Doering and a proposal for a simplified modification for the class of theories given by charged n-particle sigma-models.
Tracked: January 9, 2008 10:27 PM

Read the post L-infinity Associated Bundles, Sections and Covariant Derivatives
Weblog: The n-Category Café
Excerpt: Associated L-infinity structures are obtained from Lie action infinity-algebroids, leading to a concept of sections and covariant derivatives in this context.
Tracked: January 31, 2008 3:46 AM

Read the post Smooth 2-Functors and Differential Forms
Weblog: The n-Category Café
Excerpt: An article on the relation between smooth 2-functors with values in strict 2-groups, and an outline of the big picture that this sits in.
Tracked: February 6, 2008 12:09 PM

Read the post What has happened so far
Weblog: The n-Category Café
Excerpt: A review of one of the main topics discussed at the Cafe: Sigma-models as the pull-push quantization of nonabelian differential cocycles.
Tracked: March 27, 2008 4:45 PM

Read the post Connections on Nonabelian Gerbes and their Holonomy
Weblog: The n-Category Café
Excerpt: An article on transport 2-functors.
Tracked: August 15, 2008 8:16 PM

The n-Category Café

Skip to the Main Content

December 5, 2006