The n-Category Café

Another puzzle piece in my quest for understanding the arrow-theory of quantum mechanics, and in particular of the quantum mechanics of $n$-dimensional objects coupled to $n$-bundles with connection.

After meditating a little about how the functorial conception of quantum field theory according to Segal relates to the “AQFT” approach of Doplicher, Haag, Kastler, Roberts like the “Schrödinger picture” relates to the “Heisenberg picture”, it is time to come to terms with the true nature of the algebra of observables of the charged $n$-particle.

The $n$-particle of shape $$\mathrm{par}$$ with configuration space $$\mathrm{conf}$$ has a space of states given by the generalized elements $$\psi \in \mathrm{Hom}(1_*,\mathrm{tra}_*)$$ of the $n$-bundle with connection $$\mathrm{tra}_* : \mathrm{conf} \to [\mathrm{par},\mathrm{phas}]$$ it couples to.

(examples: the point particle, the string)

As described in the “Rosetta Stone”-section (1.2), there are three monoids naturally acting on this space of states:

1) Endomorphisms of the trivial bundle $1_*$ may be precomposed with a state $$(1_* \stackrel{\psi}{\to} \mathrm{tra}_*) \mapsto (1_* \stackrel{f}{\to} 1_* \stackrel{\psi}{\to} \mathrm{tra}_*) \,.$$ This corresponds to acting with a position operator or multiplication operator (multiplication by a function on configuration space) on the state.

2) Automorphisms of the gauge bundle $\mathrm{tra}_*$ may be postcomposed with a state $$(1_* \stackrel{\psi}{\to} \mathrm{tra}_*) \mapsto (1_* \stackrel{\psi}{\to} \mathrm{tra}* \stackrel{g}{\to} \mathrm{tra}_*) \,.$$ This corresponds to acting with a local gauge transformation on a state.

3) Flows on configuration space may be composed with a state.

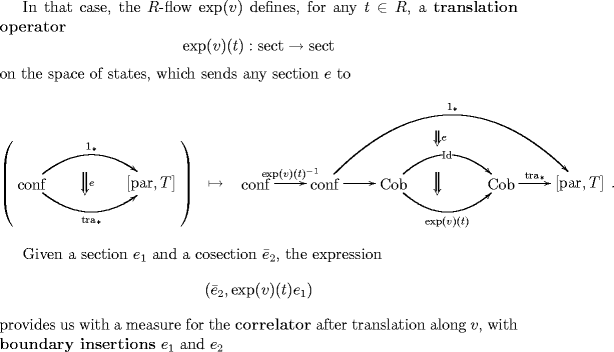
The standard example is the electromagnetically charged 1-particle on target space $\mathrm{tar} = P_1(\mathbb{R}^n)$ coupled to the line bundle $\mathrm{tra}_* \to 1d\mathrm{Vect}_\mathbb{C}$.

In this case, the space of states, $\mathrm{sect}$, is that of sections of the given line bundle. The above position operators are given by mutiplying with functions $C(\mathbb{R}^n)$. The translation operators are given by 1-parameter groups of diffeomorphisms on sections. Their differential yields the action of the covariant derivative $\nabla$ on sections, known as the (covariant) momentum operator.

For trivial line bundle this gives the familiar Weyl algebra, the algebra of observables of the free 1-particle on $\mathbb{R}^n$.

What is so very special about this? Why does nature care?

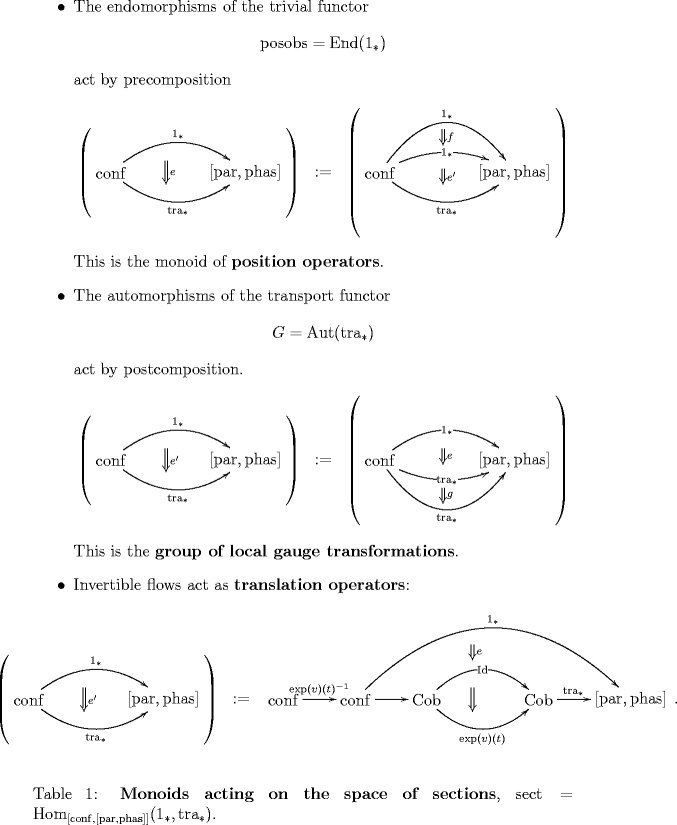
Stare at the three different actions on the space of states above for a while… precomposition of 2-morphisms, postcomposition, and whiskering.

Question: What kind of transformation is that?

Answer: A (pseudo)natural transformation!

The above three operations are unified in the following tin can equation:

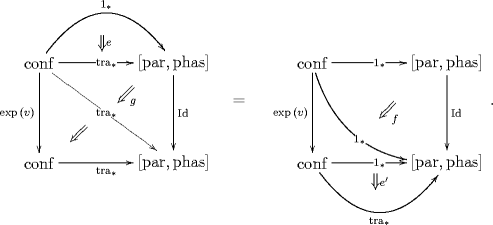
This tin can encodes: a diffeomorphism (the left vertical morphism), the covariant translation along it (the 2-cell adjacent to it), a gauge transformation (the 2-cell on top of that), and multiplication by a function on configuration space (the 2-cell on the right) – all different components of one natural operation on sections.

These are the components of a map of the space of sections $$\mathrm{sect} \stackrel{O}{\to} \mathrm{sect} \,,$$ (where I regard $\mathrm{sect}$ as an $n$-category with two objects) which is connected to the identity $$\array{ & \nearrow \searrow^{\mathrm{Id}} \\ \mathrm{sect} &\Downarrow& \mathrm{sect} \\ & \searrow \nearrow_{O} } \,.$$

We are apparently lead to

Definition: The monoid of observables of the charged $n$-particle is the submonoid of endomorphisms of the space of sections that is connected to the identity.

This neatly generalizes the way that flows along vector fields are endomorphisms of configuration space connected to the identity.

It seems that we are entitled to coin a slogan:

The algebra of observables acts on the space of states like, and generalizing how, the monoid of arrow fields acts on configuration space.

By the natural nature of everything in sight, this action automatically contains translation operators (momentum) as well as multiplication operators (position) and local gauge transformations.

If you look closely, you see that this is more flexible concerning the presence of invertibles in configuration space, thereby alleviating the issue Bruce pointed out. This may be relevant for directed configuration spaces like those discussed here.

The above figures are taken from The Charged Quantum $n$-Particle: Kinematics and Dynamics