Isham on Arrow Fields

February 8, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

Chris J . Isham
A New Approach to Quantising Space-Time: I. Quantising on a General Category
gr-qc/0303060

the author considers the concept of an arrow field on a category.

I recall his definition, reformulate it in arrow-theoretic terms, discuss the connection of “arrow fields” to ordinary vector fields and describe how to generalize it to a notion of covariant transport of sections of bundles with connection.

$MathML-enabled post (click for more details).$

Chris Isham defines (beginning of section 3.1) an arrow field on a category $Q$ as (my paraphrasing) a section of the source map. So it is an assigmnet $v : Obj (Q) \to Mor (Q)$ which sends each object $o$ in $Q$ to a morphism $o \overset{v (o)}{\to} t (v (o))$ starting at $o$ .

Here is comment on that:

we know that something which assigns morphisms to objects is likely to be a natural transformation.

Since we want this assignment to be a section of the source map, it is likely a natural transformation starting at the identity functor ${Id}_{Q}$ on $Q$ $\begin{matrix} ↗ ↘^{Id} \\ Q & ⇓^{v} & Q \\ ↘ ↗_{\exp (v)} \end{matrix}$ and ending at some endofunctor of $Q$ , which I have given the name $\exp (v)$ .

Chris Isham goes on to note that there is a natural monoidal structure on such “arrow fields”: given two arrow fields $v_{1}$ and $v_{2}$ , we obtain a new one by assigning to each object $o$ of $Q$ the composite arrow $o \overset{v_{1} (o)}{\to} t (v_{1} (o)) \overset{v_{2} (t (v_{1} (o)))}{\to} t (v_{2} (t (v_{1} (o)))) .$

Here is a comment on that:

this monoidal structure is the obvious monoidal structure on natural transformations of the above form $\begin{matrix} ↗ ↘^{Id} & ↗ ↘^{Id} \\ Q & ⇓^{v_{1}} & Q & ⇓^{v_{2}} & Q \\ ↘ ↗_{\exp (v_{1})} & ↘ ↗_{\exp (v_{2})} \end{matrix}$

Finally, in section 3.2, the author defines an action of arrow fields on objects in the obvious way: each arrow field maps an object $o$ to the target of its value at that object: $v : o \mapsto t (v (o)) .$

Here is a comment on that:

notice that this is the action of the restriction of the functor $\exp (v) : Q \to Q$ that is the target of the natural transformation $v$ .

In the last paragraph of section 3.2, Chris Isham remarks that the action of arrow fields on objects of $Q$ is like the action of the diffeomorphism group $Diff (Obj (Q))$ .

Using the above re-formulation in terms of natural transformations, we can make this precise as follows:

Let’s consider the identity component of $DIff (Obj (Q))$ and look at “smooth families” of arrow fields that contain the trivial arrow field.

So let $Q = P_{1} (X)$ be the path groupoid of a smooth space $X$ , and let $Σ (ℝ)$ be the the additive group of real numbers, regarded as a category with a single object.

Write $Flow (X) \subset Σ ({End}_{Cat} (P_{1} (X)))$ for the sub-category of endomorphisms of $P_{1} (X)$ of the form $\begin{matrix} ↗ ↘^{Id} \\ P_{1} (X) & ⇓^{v} & P_{1} (X) \\ ↘ ↗_{\exp (v)} \end{matrix},$ where everything is smooth.

As we have just seen, each of these can be regarded as defining an “arrow field” on $P_{1} (X)$ .

Notice how these arrow fields $v$ look like in this case: they assign to each point $x$ in $X$ a path $x \overset{v (x)}{\to} t (v (x))$ in $X$ . Moreover, $\exp (v) : P_{1} (X) \to P_{1} (X)$ is the functor which sends any path $x \overset{γ}{\to} y$ to $\exp (v) : (\begin{matrix} x \\ ↓ γ \\ y \end{matrix}) \mapsto (\begin{matrix} x & \overset{v (x)^{- 1}}{\leftarrow} & t (v (x)) \\ ^{γ} ↓ \\ y & \overset{v (y)}{\to} & t (v (y)) \end{matrix}) .$ We might want to think of this as the adjoint action of arrow fields on morphisms.

Now, in order to get a smooth family of such, consider smooth functors $v : Σ (ℝ) \to Flow (X) .$ These send $v : t \mapsto \begin{matrix} ↗ ↘^{Id} \\ P_{1} (X) & ⇓^{v (t)} & P_{1} (X) \\ ↘ ↗_{\exp (v (t))} \end{matrix}$ in a way that respects translation on the real line: $v (t_{1} + t_{2}) : x \mapsto x \overset{v (t_{1}) (x)}{\to} t (v (t_{1})) \overset{v (t_{2}) (t (v (t_{1}) (x)))}{\to} t (v (t_{2}) (t (v (t_{1}) (x)))) .$ And smoothly so.

I think such smooth functors $v : Σ (ℝ) \to Flow (X)$ are precisely in bijection with ordinary vector fields on $X$ .

To me, this is an arrow-theoretic notion of vector field alternative to that used in synthetic differential geometry.

If “arrow fields” on $Q$ are to be thought of as vector fields, they should act on functions on $Obj (Q)$ by some kind of translation.

At the beginning of section 4.2, Chris Isham considers the obvious action of an arrow field on a function: $v : C (Obj (X)) ∋ ψ \mapsto (o \mapsto ψ (t (v (o)))) .$

My final comment here shall be that this action of arrow fields on functions also has a nice arrow-theoretic formulation in terms of the above natural transformations. This formulation allows in particular to readily see how arrow fields act by covariant transport on sections of fiber bundles over $Obj (Q)$ , in the case where a bundle with connection over $Q$ is present. Such a covariant translation along arrow fields is conidered around equation (67) in Chris Isham’s text.

The relevant diagram, however, is a little hard to draw here. I am discussing it in section 1.2,

A Rosetta Stone: Arrow Theory of Quantum Mechanics

of the document which accompanies the discussion here.

Here is a snapshot of the end of that section:

Posted at February 8, 2007 5:38 PM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1154

82 Comments & 11 Trackbacks

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

I’ll incorporate the following comments tomorrow, when I am less tired:

The entire discussion in section 4.3 of Chris Isham’s paper amounts to saying that with the morphisms of $Q$ regarded as paths between its objects (which is the relevant interpretation for Isham’s purposes), a functor $tra : Q \to Hilb$ is a hermitean vector bundle with connection on $Obj (Q)$ .

However, this is not the way Chris Isham puts it. The connection part he calls a “multiplier” and instead of thinking of a parallel transport functor he thinks of this functor as a presheaf.

I don’t really follow the reasoning behind this. Thinking of the above functor as a presheaf would imply thinking of $Q$ as a site. But this is not the role played by $Q$ in the rest of the discussion:

$Obj (Q)$ rather plays the role of the configuration space of some physical system (and not of a site of open sets on that configuration space).

The discussion around equation (83) then amounts to noticing that a transformation $1 \to tra$ is not just a section of this bundle, but a flat section.

This is a general issue, which I also do discuss for instance in that Rosetta stone section 1.2:

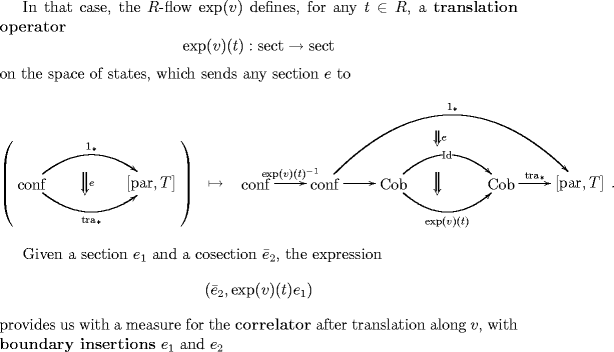
when we want to form the space of states in our arrow-theoretic formulation of quantum mechanics, we need to pass from the category of “configurations and paths between configurations”, which in my terminology is $cob = [par, tar],$ the category of functors from parameter space into target space (for the present case the parameter space is simply the point $par = •$ so that $[par, tar] ≃ tar : = Q$ )

to the subcategory $conf \subset [par, tar],$ the true configuration space, which contains only morphism between configurations that we want to regard as physically equivalent.

That’s the difference between all “cobordisms” (processes) between configurations (morphisms in $cob$ ) and the morphisms in $conf$ , which are the processes that are “pure gauge”.

So, this is why I keep going on about why specifying a physical system arrow-theoretically involves not just choosing a target space $tar$ and a bundle with connection $tra : tar \to phas$ on that, but also a sub-category $conf$ of the category of all processes in target space. That’s why I define # a physical system as a situation of the form $(par \overset{γ \in conf}{\to} tar \overset{tra}{\to} phas)$ and then give a prescription for computing the space of states which involves first pulling back $tra$ (Isham’s “multiplier”!) back to configuration space and then taking its sections.

All this is, secretly, the issue discussed around equations (83)-(84) in Chris Isham’s paper.

It’s a not a particularly complicated issue, but I think it pays to try to extract a clear picture here.

I am making this comparison with Isham’s ideas here also in the hope that it will help our mutual understanding, in the light of John’s remarks at the end of this comment.

Posted by: urs on February 8, 2007 9:13 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Urs schreibt:

instead of thinking of a parallel transport functor he thinks of this functor as a presheaf.

I don’t really follow the reasoning behind this. Thinking of the above functor as a presheaf would imply thinking of Q as a site.

One doesn’t need the notion of a site for a presheaf. A presheaf (of categories, say) on a category $C$ is simply a pseudofunctor $C^{op} \to Cat$ . The site machinery is simply to see if compatible things paste over covers. That said, Isham’s POV is still a bit mysterious, since then the “mulitplier” is a presheaf on $Q^{op}$ .

Posted by: David Roberts on February 9, 2007 12:49 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

One doesn’t need the notion of a site for a presheaf.

Sure, right. But given any contravariant functor, you would not call it a presheaf unless you are going to think of its domain as a site.

My point is just this:

of course, since a presheaf is nothing but a contravariant functor, Isham is free to call his contravariant functor a presheaf – but it is not a natural point of view on the situation he considers. I think.

On the other hand, if we think of this functor (contravariant or not is not that important, since in standard applications the domain is a groupoid anyway) as the parallel transport of a bundle with connection, then everything falls into place.

Posted by: urs on February 9, 2007 7:38 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

Hi everyone

One of my PhD students just drew my attention to this site. Perhaps I may add a few remarks to the discussion.

Firstly, there seems to be some confustion between a sheaf and a pre-sheaf: it is the former that requires a site; a presheaf on a category C is simply defined to be a functor from that category to the category Set, there is no need for a Grothendieck topology. At least, that is the definition that is used by all texts on topos theory:-)

When writing my paper I was well aware of the similarity to a connection. Indeed that was part of the original motivation. I saw my work as a big generalisation to a categorial context of Mackey’s work on induced representations of semi-direct product groups . There are two ways of seeing what a Mackey representation looks like. One is in terms of a principal bundle and associated vectors bundles: if you like, that is the ‘differential geometry’ route. Various (flat) connections can arise naturally in this approach.

However, there is another approach which Mackey himself favoured, and this is more functional analytic in form(in fact, I am not sure if Mackey even realised there was a fibre bundle version). In particular, even if the underlying principal bundle is non-trivial, there still exist measureable cross-sections (although, of course, no smooth ones). Mackey used such such to ‘de-bundlise’ (:-)) the construction and, when you do that, the ‘multiplier’ appears naturally from the representation of the isotropy group used in the representation of the semidirect product.

I decided to generalise Mackey’s, measure theoretical, approach rather than the differential geometry one because, in my case, the base space is the objects in the category, and this is far from being a manifold.

Actually, the referee of my paper remarked approvingly (I think:-)) that what I was really doing was constructing a vast generalisation of Mackey theory.

Of course, there are more ways of ‘skinning a cat’ as the old English proverb goes, and it is always good to look at something in more than one way.

Kind regards to all

Chris Isham

Posted by: Chris Isham on February 15, 2007 6:21 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Dear Chris Isham,

many thanks indeed for your comment!

I very much like the philosophy of your approach of “quantizing on a category”. Essentially, one should consider a quantum system as living on the category of paths (“trajectories”, “histories”) in its configuration space.

Without really being aware of your work, I have spent lots of time lately thinking about something very similar #.

My motivation was mainly to understand how a functor characterizing some kind of parallel transport of some physical object gives rise to the functor that describes the quantum propagation of that very object.

For that reason I felt particularly sensitive concerning your remarks on that structure you call a “multiplier”. Therefore my corresponding remark.

You write:

Firstly, there seems to be some confusion between a sheaf and a pre-sheaf: […]

David Roberts raised that point already. I don’t really think there is any confusion concerning the math. But maybe there is some difference in the phiosophy concerning terminology. I had replied to David’s (and now your) remark here.

What I think is helpful is to consider the general idea of “quantizing on a category” for simple familiar examples, like the free non-relativistic particle. Understanding that well enough would help me with applying the same formalism to more ambitious tasks, like quantizing general relativity by considering a configuration space category of posets representing spacetimes, as you do in gr-qc/0304077.

For the single nonrelativistic particle propagating on some target space $X$ , we would take the “category that we quantize on” to be the category whose objects are the points in target space (the configurations of our particle) and whose morphisms would be some suitable kind of paths (for instance smooth Moore paths) in $X$ .

If the particle is “charged”, under an electromagnetic field, say, there would in addition be a parallel transport functor # in the game, which sends each such path to the corresponding phase change of the particle caused by that background field.

Given that, there is, I think, a canonical arrow-theoretic way to send this “classical” data to the corresponding quantum theory:

For instance the space of states of the particle would be obtained by restricting the parallel transport to constant paths in $X$ and then “pushing it to a point”. This produces # the space of sections of the (potentially nontrivial) vector bundle that represents the background field (a line bundle in the case of electromagnetism).

On that space of states, we can naturally act with certain correspondences, coming from restricting a piece of worldline of the particle to its endpoints. This does reproduce the familiar propagator of our charged particle #.

It is this setup, together with similar consistency checks for more interesting cases, that provides a certain confidence in the interpretation of the various abstract ingredients that go into “quantizing on a category”.

For instance, I believe this does shed light on the issue that you are dealing with in particular in gr-qc/0306064, where you notice that if the “category we quantize on” has Hom-sets with more than one element, then the interpretation of these morphisms as inducing momentum operators breaks down.

Judging from the example of the single particle mentioned above, a reason for this apparent problem is suggested: the morphisms correspond in general to arbitary paths that the “system” (here: the particle) may trace out as it evolves. Only the “infinitesimally short” such paths would induce momentum operators of the kind they appear in, for instance, equation (1.2) and (1.3) of gr-qc/0306064.

I believe this can be made precise as follows: as I indicate in the entry above, there is a way to identify the “arrow fields” that you consider with true vector fields in the case that we have smooth functors which I denoted $v : Σ (ℝ) \to Flow (X)$ above.

One can see that these describe the flow along a vector field $v$ on $X$ . These flows act on the states of our system in a natural way. Differentiating this action with respect to the single paramter defining the flow gives the familiar action of the momentum operator associated to the vector field $v$ .

It is this differentiation process which evades the problem you mention, that many paths may go between to given points: as we differentiate, all paths starting at a given point in the limit look like tangent vectors emanating radially away from that point.

Of course all this applies directly only when we have a smooth structure on our category, which does allow us to perform this differentiation.

For the example of the free particle we do. For many other examples, too.

But we might imagine applying that formalism even to examples where the configuration space category of our system does not have a sensible smooth structure.

As far as I understand, this is certainly the case for the categories of posets that you consider.

I would still think, though, that we get “momentum operators” even in these cases from looking at group homomorphisms $Σ (G) \to Flow (X)$ (noticing that the way the category $Flow (X)$ is constructed it exists quite generally).

For instance, we might imagine that the configutration space category of our system is a discrete cell complex. The morphisms of the “category we quantize on” would be generated from edges of some underlying graph, say.

In such a situation, we might take $G = ℤ$ the integers, and consider vector fields on configuration space to be group homomorphisms $Σ (ℤ) \to Flow (X) .$ Noticing that $Σ (Z)$ is the groupoid freely generated from the graph containing a single edge, we might demand this to even be a graph map.

If we do so, we do recover a discrete analog of differentiability: the above group homomorphism will send a single parameter step in $ℤ$ to an “elementary” morphism in the category we are quantizing on. If the edges of the underlying graph for instance locally form a cubical lattice, there will locally only be unique paths between pairs of points and we again retrieve a well-defined notion of momentum operator.

I am aware that this example of “quantization on a graph category” might not be directly relevant to the categories of poses that you consider. But I did mention it to indicate how the intuition that can be gained from “quantization on a category” of the single point particle suggests how to deal with more general cases.

Well, or so I think. You have certainly thought longer about these issues than I have, so maybe you would rather disagree with what I say here.

If so, please do! I’d be very interested in your comments.

Posted by: urs on February 16, 2007 11:23 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Allow me to join in the fun and make some comments too :-) Some of these comments are just rehashes of stuff I said earlier $pic$ in response to John’s comments - these latter are certainly relevant for our current discussion!

Firstly, I found the idea of an “arrow field” on a category an interesting idea. It seems so simple, I thought it was strange I personally had never actually encountered this idea while reading about categories and physics. Thats embarassing for me - I’m sure the n-cafe hosts thought about these things when they were toddlers ;-)

Perhaps I hadn’t seen it before because its not a particularly invariant construction : two equivalent categories will have different monoids of arrow fields. For example, the action groupoid $G$ of $ℤ_{2}$ on a two element set is equivalent to a one object groupoid $ℤ_{2}$ , while

(1)

Arr (G) = (ℤ_{2})^{8}, Arr (ℤ_{2}) = ℤ_{2} .

(I think!)

Anyway, I still find it a bit weird. Lets work it out in simple examples. Suppose a finite group $G$ acts from the left on a finite set $X$ . As usual, one thinks of this via the action groupoid $G_{G} (X)$ , [ Ed : how do you get calligraphic letters? ] whose objects are elements $x \in X$ with morphisms $g \cdot x \overset{g}{\leftarrow} x$ depicting the action of $G$ on $X$ .

Now let $Arr (G_{G} (X))$ be Chris Isham’s group of arrow fields . An arrow field is a choice of an arrow emanating from each object $x$ , and you compose them in the obvious way.

In our example, it consists of set-wise maps $s : X \to G$ with the composition law

(2)

s_{1} * s_{2} (x) = s_{1} (s_{2} (x) \cdot x) .

This seems such a fundamental example I find it a bit emabarassing that I had never thought about this before : that the set of maps from $X$ to $G$ forms a group $pic$ .

Secondly, suppose we’re given a finite groupoid $G$ and a representation $ρ : G \to Hilb$ , which we think of as a vector-bundle-with-connection over $G$ . (Hint to first-timers : everyone at the n-cafe knows that I go on and on about representations of finite groupoids, ever since my supervisor published a paper about these issues).

Given the representation $ρ$ , we have the space of sections $Γ_{G} (ρ)$ , and the space of flat sections $Γ_{G}^{0} (ρ)$ . The former is what Chris Isham calls the ‘space of states’, at least in his first two papers.

Now the arrow fields $Arr (G)$ act on the space of sections $Γ_{G} (ρ)$ . The corresponding thing which acts on the flat sections $Γ_{G}^{0} (ρ)$ is the (objects of) the automorphism 2-group $Aut (G)$ of $G$ . (The full automorphism 2-group acts on $Rep (G)$ ).

Thirdly, Chris Isham defines an inner product on the space states $Γ_{G} (ρ)$ by

(3)

(s_{1}, s_{2}) = \sum_{x \in Ob (G)} (s_{1} (x), s_{2} (x))

where these latter inner products are taken in the Hilbert spaces $ρ (x)$ . He mentions that “it is necessary to develop a proper measure on the set $Ob (G)$ ”.

Indeed! That is precisely what all of us at the n-cafe were talking about in the discussion of Tom Leinster’s Euler characteristic of categories.

In the case when $G$ is a groupoid, the appropriate measure to use is $\frac{1}{∣ x \to ∣}$ . Thus the inner product on the space of sections should be modified to

(4)

(s_{1}, s_{2}) = \sum_{x \in Ob (G)} \frac{(s_{1} (x), s_{2} (x))}{∣ x \to ∣} .

When $G$ is a poset, its also well known what measure to use (see Tom Leinster’s paper).

Finally, in Chris’s third paper he suggests that an alternative definition of the space of states of a category $G$ would be as functions on the space of arrows. This is nothing but $ℂ [G]$ , using John’s notation from this post.

In conclusion : Chris Isham’s ideas mesh well with the stuff n-cafe folks have been talking about!

Posted by: Bruce Bartlett on February 16, 2007 6:58 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

For example, the action groupoid $G$ of $ℤ_{2}$ on a two element set is equivalent to a one object groupoid $ℤ_{2}$ , while $Arr (G) = ℤ_{2}^{8} Arr (ℤ_{2}) = ℤ_{2}$

Isn’t $G$ the codiscrete category (precisely one morphism for every ordered pair of objects) on two objects? Doesn’t that give four different arrow fields on $G$ ?

it’s not a particularly invariant construction

I suggested to think of arrow fields as natural transformations starting at the identity endomorphism on our category. That’s manifestly invariant under equivalence. (You would probably enjoy to think of this as an element of the 2-trace of an endomorphism of our category :-)

“it is necessary to develop a proper measure on the set $Ob (G)$ ”.

Indeed! That is precisely what all of us at the $n$ -cafe were talking about in the discussion of Tom Leinster’s Euler characteristic of categories.

In the case when G is a groupoid, the appropriate measure to use is $\frac{1}{∣ x \to ∣}$

Hm, sure? Makes me a little nervous that the measure is supposed to be determined by topology alone. That’s not how it works for ordinary quantum mechanics! I may be wrong, but consider this:

In the case of ordinary quantum mechanics of a point particle, we would want the measure on the space of objects to be that coming from a Riemannian metric on that space.

Remarkably, for ordinary quantum mechanics we also choose a measure on the space of morphisms. Namely the Wiener measure (or rather its complex version) associated to the Riemannian metric on the space of objects.

Posted by: urs on February 16, 2007 10:19 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Urs wrote:

Isn’t G the codiscrete category…?

Yes - thanks! Sorry, I suppose I meant $ℤ_{2} \oplus ℤ_{2}$ acting on a 2-element set. You know what I mean - two objects, four morphisms going out from each object.

You suggested thinking of arrow fields as natural transformations starting at the identity endomorphism. I suppose this only works when the category is a groupoid. Nevertheless its a very helpful point of view! Its weird : it says that an arrow field on a category is the same as a single arrow in another category. Heh its obvious I suppose, but one needs to enjoy the small things in life.

Posted by: Bruce Bartlett on February 17, 2007 12:45 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

You suggested thinking of arrow fields as natural transformations starting at the identity endomorphism. I suppose this only works when the category is a groupoid.

It will coincide with the more component-based notion of arrow field as “section of the source map” if the category is a groupoid.

If the category is not a groupoid, transformations starting at the identity endomorphism may still exist, but there may be less of them than there are sections of the source map.

Its weird: it says that an arrow field on a category is the same as a single arrow in another category

Yes, but notice that to some extent this is just what happnes when you put that monoidal structure on arrow fields and then realize than any element in a monoid is equivalently an arrow in a category with a single object.

Posted by: urs on February 18, 2007 12:25 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

You suggested thinking of arrow fields as natural transformations starting at the identity endomorphism. I suppose this only works when the category is a groupoid.

It will coincide with the more component-based notion of arrow field as “section of the source map” if the category is a groupoid.

By the way, in this context, a natural transformation starting and ending at the identity endomorphism on our category would define a loop field on the category: a choice of loop over every object.

Posted by: urs on February 20, 2007 9:12 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

I am at the airport on my way to Sweden, where I will visit Jens Fjelstad in Karlstad. On my way to the airport, I had the leisure to think.

Above, Bruce declared that the mysterious measure we have to invoke in order to do the path integral (when we “quantize on a category”) is always the weighting of the kind we have been discussing.

This is certainly true – and well known – for topological field theories, like Dijkgraaf-Witten theory.

Still, I objected to the statement in its generality, pointing out that for simple non-topological systems like the ordinary free particle, the measure instead derives from a measure induced by a (pseudo-)Riemannian metric on some target space.

Now I realize that this is not a contradiction at all! Both statements should be right.

The weighting should be the general “right” measure, because it somehow models the results one would obtain had one replaced $ℂ$ by $ℂ Set$ and computed an ordinary colimit.

If, for instance, we assume that that the automorphism group at some vertex acts freely on these sets, then indeed their colimit has cardinality given by the original cardinality divided by the numer of automorphisms.

(There should be a better way to say this. I will re-read some stuff Tom Leinster recently wrote and then maybe try to say the above again, in more generality. Possibly I am only now beginning to fully appreciate the impact of Tom’s idea to the program of arrow-theoretic quantization.)

So, if we expect a certain measure to appear in a certain example, we should probably try to understand the true category of configurations of that example! For the right choice of category, the canonical “weighting”-measure should then coincide with the one we are expecting to see.

On my way to the airport I played around with various discretizations of the free particle, which were such that the canonical groupoid measure reproduced the Wiener measure on paths in an appropriate limit.

If everything is right, the Wiener measure should in fact be (maybe a suitable continuum limit) of a weighting on a category whose objects are parameterized paths in some Riemannian space and whose morphisms are certain automorphisms of these paths – for instance certain notions of reparameterizations.

I think this can be done, but none of the solutions I found looks particularly natural or elegant.

I imagine chances are higher that we find a nice natural structure for the relativistic free particle.

So, consider the poset ${worldvol}_{n} = 1 \to 2 \to \dots \to n$

as a model for a worldline (of “parameter length $n$ ”) of a particle.

Moreover, let $M^{d}$ be $d$ -dimensional Minkowski space, choose some sub-lattice of that and consider it as a poset ${tar}_{M^{d}}$ by demanding that $x \to y$ if and only if $y$ is in the future of $x$ . (This is how Sorkin and Isham model spacetimes by posets.)

Now, the category of all histories $hist = [{worldvol}_{n}, {tar}_{M^{d}}]$ is again a poset. An object is a timelike path of $n$ straight steps in spacetime.

A morphism beween two such paths with fixed endpoints describes how to push the source path closer to the lightcone. $hist$ is itself a poset.

Question: What is the weighting on the subcategory ${hist}_{x}^{y}$ of all paths whose endpoints sit at some fixed points $x$ and $y$ in target space? How does it behave asymptotically for large $n$ ?

(Guess what I am hoping the answer will be…)

Posted by: urs on February 22, 2007 9:02 AM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

This conversation is way over my head, but something you said made me think you were somehow relating connectivity on a graph (via weighting) and geometry (via Reimannian measure). Did I totally miss the mark? That would resonate with a few thoughts stashed away in the back of my mind somewhere.

Posted by: Eric on February 22, 2007 2:27 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

The connection I’m thinking of is more like:

randomness -> geometry

but the weightings have an interpretation as generating “random motion on a graph”, so the neat link would be

weighting -> randomness -> geometry

Is that vague enough for you? :)

Posted by: Eric on February 22, 2007 2:31 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Yes, somehow this amounts to something that we have vaguely been thinking of before: the structure of the morphisms induces a measure on the space of objects.

Above I was considering this phenomenon on the space of “paths” of a physical system. But if that is the way it seems to be, one would certainly be tempted to apply the same sort of reasoning to categories modeling spacetime itself.

So if we decide to model pseudo-Riemannian spacetime as a poset (with arrows connecting those points that can be connected by a timelike or lightlike travelling particle), i.e. if we specify a light cone structure on spacetime, then Tom Leinster’s formula (for the case that everything is finite at least) actually provides us, for free, also with a volume measure on that spacetime.

Let’s see, how was that: light-cone structure together with volume is almost the same structure as a (pseudo-)Riemannian metric. Right?

Posted by: urs on February 22, 2007 5:16 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Urs wrote:

Question: What is the weighting on the subcategory $hist (x, y)$ of all paths whose endpoints sit at some fixed points $x$ and $y$ in target space?

After reading this, I tried my hand at solving it, but I sadly failed $pic$ . It brings up the following questions about Tom’s paper:

(a) Given finite categories $X$ and $Y$ with weightings (and coweightings), is there a weighting on $[X, Y]$ ?

(b) Suppose a category $X$ has a weighting. What can we say about the existence of a weighting on some full subcategory $A \subset X$ ?

I’m sure I’m embarassing myself here $pic$ … but I didn’t know the answer to these, and failed to find the answer explicitly written in bold letters in Tom’s paper. For (a), I tried the formula

(1)

w_{[X, Y]}^{F} = \sum_{x \in X} w_{Y}^{F (x)}

which tries to calculate the weighting on $[X, Y]$ in terms of that on $Y$ . “ $F$ ” stands for a functor $F : X \to Y$ .

I also tried one of the form

(2)

w_{[X, Y]}^{F} = \sum_{x \in X} \frac{w_{Y}^{F (x)}}{w_{X}^{x}}

which tries to use both the weightings on $X$ and $Y$ . Sadly, I couldn’t make headway.

In reply to (b), note that just restricting the weighting on $X$ to $A$ doesn’t work : in general there will be arrows emanating from $A$ to $X$ , even though $A$ is a full subcategory.

I think Urs’s idea of a measure on paths (with fixed endpoints) in posets, using Tom’s weightings, is a nice idea - it also ties in with something John wrote recently about inegrating over $hom (a, b)$ . Probably I’m revealing some sad misunderstanding about the Euler characteristic in my questions above, but if so, there are probably others like me in the same boat!

Posted by: Bruce Bartlett on February 22, 2007 5:45 PM | Permalink | Reply to this

Re: Isham on Arrow Fields

$MathML-enabled post (click for more details).$

Just a few more thoughts regarding the above. Urs has suggested that when trying to calculate the classical path integral

(1)

〈 b ∣ U (t) ∣ a 〉 = \int_{paths γ : a \to b} e^{- S [γ]} D γ

that the appropriate measure to use on $Paths (a, b)$ - the space of paths $γ$ from $a$ to $b$ - is given by Tom’s weightings on the category $Paths (a, b)$ :

(2)

e^{- S [γ]} D γ = w^{γ} .

Okay, thats at least my interpretation - perhaps lousy - of what Urs is actually saying.

In particular, the path integral computes as the Euler characteristic of $Paths (a, b)$ :

(3)

\int_{paths γ : a \to b} e^{- S [γ]} D γ = χ (Paths (a, b)) .

To be precise, we talk about paths in a poset called “tar” for target space, which we think of as functors $γ : {worldvol}_{n} \to tar$ where

(4)

{worldvol}_{n} = 1 \to 2 \to \dots \to n .

We set $Hist : = [{worldvol}_{n}, tar]$ . The question is, what is the weighting on $Paths (a, b)$ - the full subcategory of Hist consisting of paths such that $γ (1) = a$ and $γ (n) = b$ ?

It seems there are three answers (see my questions above):

1. Use the weighting restricted from Hist. Its not a weighting on Paths(a,b), but who cares! Sum it up and see what happens.

2. Paths(a,b) is itself a poset, and we can calculate a weighting for it. Use this.

3. Do something else.

If you use option (2), then the path integral always is 1, for any $n$ and for any $a, b \in tar$ . That’s because the path $(a b b \dots b)$ is a terminal object in $Paths (a, b)$ . Thus the Euler characteristic of $Paths (a, b)$ is 1.

If you use option (1), my intution is that the path integral always gives zero. That’s because inside Hist, there is always a morphism $(a b b \dots b) \to (b b b \dots b)$ .

Posted by: Bruce Bartlett on February 22, 2007 7:13 PM | Permalink | Reply to this

measure on paths

$MathML-enabled post (click for more details).$

Urs has suggested […]

That’s the nice thing about discussions: ideas arise that none of the individuals would have come up with by themselves. Here we see Bruce attributing an idea to me which I was attributing to him. Apparently it was given to us from elsewhere… :-)

If you use option (2), then the path integral always is 1

Right! So that’s not what we want.

I tend to think that what we should really be looking at is more like your option (1), where the measure is that induced by the measure on free paths.

To figure this out, we should think properly about which procedure we really ought to be looking at: there is a general pull-push process of quantization, which, as you know, I tried to formulate in the arrow-theoretic terms needed here.

When you look at this prescription, you see that it involves a push-forward operating on all of $hist$ in a certain way.

I should try to work that out in more detail for the case of hand where ${worldvol}_{n} = 1 \to 2 \to \dots \to$ and $tar$ is a “causal poset” of Minkowski spacetime.

A formula which might be helpful for doing this is the one Tom Leinster mentions here.

Posted by: urs on February 23, 2007 8:18 AM | Permalink | Reply to this

Re: measure on paths

$MathML-enabled post (click for more details).$

I wrote:

To figure this out, we should think properly about which procedure we really ought to be looking at

Okay, so when doing this pull-push, what we seem to end up computing (but see below) is, for each point (object) in target space, an integral over all paths ending at that point, namely over the pullback of some state to these paths times a phase associated to the paths: $ψ (y) = \int_{t^{- 1} (y)} tra (x \overset{γ}{\to} y) (ϕ (x))) e^{- S_{kin} (γ)} D γ .$ As before, $e^{- S_{kin} (γ)} D γ$ would be the measure on the space of paths, which we would like to see if it can be understood as a weighting on the category of these paths in a suitable way.

(I write $S_{kin}$ to emphasize that it is really just the so-called “kinetic” part of the action which is supposed to be part of the measure on the space of paths. In the above formula, for instance, $tra (γ) : = e^{i S_{bg} (γ)}$ is the (exponentiated) action corresponding to the coupling to the background gauge field encoded by the functor $tra$ .)

So it would seem we should be looking for the measure on the full subcategory ${hist}^{y} \subset [{worldvol}_{n}, {tar}_{M^{d}}]$ of all paths ending at some point $y$ .

Sadly, this category still has a terminal object, namely the constant path sitting at $y$ . This, as Bruce remarked, would imply that we have a weighting which is concentrated entirely on that constant path (all others having weight 0).

But, on the other hand, the above is still not quite what we are supposed to be looking at. Rather, we should be looking at the pull-push of transformations $e$ through $\begin{matrix} hist \times worldvol \\ ^{{out}^{*}} ↙ & ↘^{{in}^{*}} \\ conf \times par & \Leftarrow & conf \times par \\ _{ev} ↘ & ↙_{ev} & ↓ \\ tar & ↓ \\ tra ↓ & \overset{e}{\Leftarrow} & ↓ \\ phas & \leftarrow \end{matrix},$ for the case that $phas =_{FinSet} Mod,$ as I described here.

When you write out what this means (best for the simple case where $tra$ is a trivial line bundle and hence assigns the canonical 1-dimensional $FinSet$ -vector space to each point, i.e. $FinSet$ itself), you find that this leads to a colimit on a functor on the category of paths which takes values not quite in $FinSet$ itself, but in a version of $FinSet$ where morphisms may be “twisted” in a certain way!

Hm…

Posted by: urs on February 23, 2007 10:34 AM | Permalink | Reply to this

Re: measure on paths

$MathML-enabled post (click for more details).$

I have thought a little more about this issue of finding a lift of a measure set to a category such that a weighting on the category exists and reproduces the original measure on the space of objects.

I would like to see if this can be applied to posets modelling pseudo-Riemannian spacetime (inspired by these ideas).

In the above above we did run into some first problems.

Pausing for a moment and reflecting on what might have gone wrong in these attempts, I noticed that already my model for the 1-dimensional space was severely broken. Fixing this might be a key to making progress.

Namely, I said I wanted to consider the poset ${worldvol}_{n} = {1 \to 2 \to 3 \to \dots \to n}$ as a model for the interval $[0, n] \subset ℝ$ .

But that badly fails in modelling the standard measure on $ℝ$ : since ${worldvol}_{n}$ has a terminal object, $n$ , it has a weighting which is 1 at that object and 0 elsewhere. So from the point of view of measure the space ${worldvol}_{n}$ is no different than a single point.

In the context of the exercise we are doing here, this should mean that we have to throw in additional morphisms unti we do get the weighting we desire.

On the other hand, we don’t want to ruin the poset-nature of ${worldvol}_{n}$ , in order to retain the nice physical interpretation that we are after.

I think there is one nice and natural way out: we pass to a mild blend between a poset and a groupoid!

So let’s consider categories which have at most one morphsim going between different objects, but where each object may have nontrivial automorphisms.

This implies that composing every automorphism with a non-automorphism just reproduces that non-automorphisms. So we do can consistently put nontrivial automorphism group on the objects of a given poset and still have a category.

So consider a new category $worldvol'_{n}$ which is generated from the poset $1 \to 2 \to \dots n$ and a vertex group of order $i$ on the $i$ th object, subject to the relation that composing any automorphism with a morphism coming from the poset just reproduces the latter.

Then it is easy to see (calculating backwards from the object $n$ ) that a weighting on this category is given by the constant function which sends every object to $1 / n$ .

This is indeed the weighting that resembles the standard measure on the interval $[0,1]$ .

One can proceed completely analously for causal posets obtained from finite truncations of lattices inside $d$ -dimensional Minkowski space, and probably for any causal subset of any pseudo-Riemannian manifold. Adding suitable automorphisms groups to the objects allows one to pretty much arbitrarily adjust the weighting at that object.

So let $tar'_{M^{d}}$ be a category of this kind. Then we should redo the exercise we discussed above and try do understand the induced weightings on the functor category $hist = [worldvol'_{n}, tar'_{M^{d}}] .$

I haven’t managaed to make any progress on that yet, but at least the full subcategories ${hist}^{y} \subset hist$ of paths that end at some point $y$ in target space no longer contain a terminal object and hence have a chance of carrying a non-pathological weighting.

In closing, I’ll mention the following observation:

By throwing in all those extra automorphisms into our poset, we are effectivly enlarging the automorphims group of the identity endofunctor on our poset.

In a slightly different but rather similar context, such automorphisms, have been addressed as supersymmetries.

Not sure what this means, but maybe something to keep in mind.

Posted by: urs on February 24, 2007 12:43 PM | Permalink | Reply to this

Re: measure on paths

Hi Urs,

Would you mind writing one or two sentences describing what you are trying to do in terms even I can understand? You guys are way over my head at the moment, but occasional I read something that resonates with things I’ve thought about. For example, it almost seems like you are trying to build a discrete model for R. I’m probably just confused…

Eric

Posted by: Eric on February 24, 2007 4:33 PM | Permalink | Reply to this

Re: measure on paths

$MathML-enabled post (click for more details).$

Hi Eric,

Would you mind writing one or two sentences describing what you are trying to do in terms even I can understand?

I’ll try to do that!

Essentially everything in the game here is quite elementary (except possibly for the proof of Tom’s theorem, but the statement of the theorem is certainly elementary), so if you feel that

You guys are way over my head at the moment

then this is certainly a defect on “our” side (my side, more likely).

So, this is the idea:

As you know better than I do, some people are fond of the idea that pseudo-Riemannian spaces can equivalently be thought of as posets equipped with a measure.

As for instance described in

Rafael Sorkin, Causal Sets: Discrete Gravity .

Now, along comes Tom Leinster with a theorem which says that for a given category there is, under some conditions at least, a natural notion of measure induced by the set of morphisms on the set of objects.

What is so very nice about this measure it that it translates colimits of functors over that category into integrals of functions over the objects of that category.

Maybe you’re not familiar with the notion of colimit. But never mind for the moment and just accept that this is an interesting property. The upshot is that the morphisms of a category (under suitable conditions) do induce in a god-given way a measure on the space of objects.

Now, people around Sorkin have tried to induce a measure on their posets by considering their elements to be embedded into some space and measuring their density there.

But I am now saying: given Tom Leinster’s result, there is a much more intrinsic and more natural way to think of our poset as being equipped with a measure (see this comment by Tom Leinster for what is so good about this, and maybe my remark on why this might be interesting for physics).

Or almost. To get measures of the kind we expect to see using Tom’s result, it turns out that we need to modify the space of morphisms of the poset a little.

Above, I was talking about how one can take a poset and add to it lots of automorphisms (invertible arrows that start and end at a given point) such that the measure induced on these points by Tom’s theorem is more like the kind of measure we expect to see (less pathological than when we don’t do this).

Ah, by the way, maybe the term “measure” is confusing here: it is really just a fancy word, meant to be suggestive but being total overkill: we are really talking about finite sets. A measure on that is just a function that assigns a weight to each point – a number that we want to think of as the “volume” associated with this point.

So, all you need to know in order to participate in this game is what Tom’s theorem says how such an assignment of numbers is induced by a collection of morphisms on our set.

The definition is indirect: we say that a function $w : x \mapsto w (x)$ on our set of objects is a measure induced from the morphisms on these objects, if for every object $x$ the following condition holds: $\sum_{y} ∣ Hom (x, y) ∣ w (y) = 1 .$ Here the sum is over all objects and the term $∣ Hom (x, y) ∣$ just denotes the number of morphisms from $x$ to $y$ .

For simple examples of categories, it is easy to solve this equation recursively by working backwards from objects that have very few outgoing morphisms.

If you need some simple examples, try Tim Silverman’s discussion here (but beware that he is talking about coweightings, where we replace $Hom (x, y) \leftrightarrow Hom (y, x)$ ).

So, for instance, for the category with two objects and a single nontrivial morphism going between them $0 \to 1$ the weighting is $w (1) = 1$ $w (0) = 0$ Notice that there is an identity-morphism on every object which we do take into account. So there is one morphism emanating from $1$ and two from $0$ .

Now, this weighting is not what we expect to be a discrete version of the standard measure of the interval $[0,1]$ .

But now throw in one additional morphism $1 \overset{f}{\to} 1$ and require that $1 \overset{f}{\to} 1 \overset{f}{\to} 1 = 1 \overset{Id}{\to} 1$ and that $0 \to 1 \overset{f}{\to} 1 = 0 \to 1 .$

This way, we now have two morphisms emanating from 1, both having the object 1 as target. This implies that now $w (1) = 1 / 2 .$ Also, there are still only two different morphisms emanating from 0, one of them being now weighted by $1 / 2$ . It follows that also $w (0) = 1 / 2 .$

This way, we do indeed recover the obvious discretization by two elements of the standard measure on the interval $[0,1]$ .

Posted by: urs on February 24, 2007 6:41 PM | Permalink | Reply to this

Re: measure on paths

$MathML-enabled post (click for more details).$

And so on.

So what I called ${worldvol}_{3} = {1 \to 2 \to 3}$ is the category with three objects $1,2,3$ and nontrivial morphisms $1 \to 2$ $2 \to 3$ and $1 \to 3$ such that $1 \to 2 \to<$

The n-Category Café

Skip to the Main Content

February 8, 2007