Common Applications

December 21, 2006

Posted by David Corfield

I’ve been reading some of Jorg Lemm’s papers in recent days. He’s written a book - Bayesian Field Theory - which I don’t have access to, but he had written a paper of the same name earlier. In it (page 6, note 1) he remarks that:

statistical field theories, which encompass quantum mechanics and quantum field theory in their Euclidean formulation, are technically similar to a nonparametric Bayesian approach.

It is intriguing to see so many constructions of mathematical physics - mean field methods, diffusion models, free energy - find a use in learning theory. But what to make of it? If we think it needs an explanation at all, we might say that perhaps it’s telling us that we only have a limited number of tools, so should expect to use them time and again. If we were washed up on a desert island with just a knife in our pocket, we’d find a host of uses for it, with little in common between them, e.g., opening a clam and sharpening a stick.

David Ruelle favoured this kind of explanation about multiple application in “Is our mathematics natural? The case of equilibrium statistical mechanics.” Bull. Amer. Math. Soc. 19, 259-268 (1988). Our minds have a limited repertoire, which explains why mathematicians keep bumping into the same constructions. Closer to this blog, a similar question is why the deeper reaches of number theory (Langlands programme) and quantum field theory (duality) are so closely related. In Mathematics in the 20th Century, Michael Atiyah’s predictions for the 21st century went thus:

What about the 21st century? I have said the 21st century might be the era of quantum mathematics or, if you like, of infinite dimensional mathematics. What could this mean? Quantum mathematics could mean, if we get that far, ‘understanding properly the analysis, geometry, topology, algebra of various non-linear function spaces’, and by ‘understanding properly’ I mean understanding it in such a way as to get quite rigorous proofs of all the beautiful things the physicists have been speculating about.

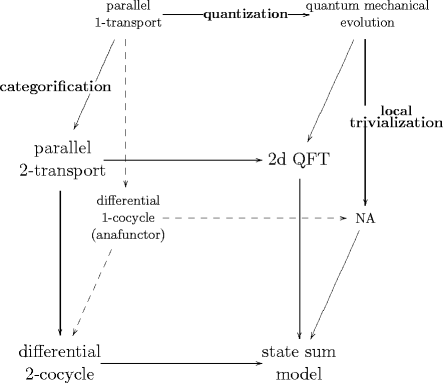
This work requires generalising the duality between position and momentum in classical mechanics:

This replaces a space by its dual space, and in linear theories that duality is just the Fourier transform. But in non-linear theories, how to replace a Fourier transform is one of the big challenges. Large parts of mathematics are concerned with how to generalise dualities in nonlinear situations. Physicists seem to be able to do so in a remarkable way in their string theories and in M-theory…understanding those non-linear dualities does seem to be one of the big challenges of the next century as well. (Atiyah 2002: 14-15, my emphasis)

Again, is this just a sign of our limited repertoire? (Perhaps Atiyah might have said that the problem is also how to categorify such dualities.)

A second strain of explanation for multiple application of a piece of mathematics, on the other hand, is that the things it is applied to really are similar. It is no accident that the same tools work in different situations when the tasks are very similar. With regards to commonalities between Bayesian statistics and physics, Edwin Jaynes would favour this latter explanation. Recently this has been expressed by Caticha in The Information Geometry of Space and Time:

The point of view that has been prevalent among scientists is that the laws of physics mirror the laws of nature. The reflection might be imperfect, a mere approximation to the real thing, but it is a reflection nonetheless. The connection between physics and nature could, however, be less direct. The laws of physics could be mere rules for processing information about nature. If this second point of view turns out to be correct one would expect many aspects of physics to mirror the structure of theories of inference. Indeed, it should be possible to derive the “laws of physics” appropriate to a certain problem by applying standard rules of inference to the information that happens to be relevant to the problem at hand.

Noting that statistical mechanics and quantum mechanics can be largely constructed by considering them as ways of manipulating information, Caticha goes on to take on general relativity.

Now, John Baez raises an interesting example of commonality of structure in this comment, between natural selection and Bayesian inference. I could imagine explanations by both of the strains above.

The structure of Bayes’ theorem (which doesn’t require you to be a Bayesian to use) is a very simple one relevant in many combinatorial situations, which is how we like to think about the world.
Evolution is a kind of learning.

Posted at December 21, 2006 3:14 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1084

15 Comments & 3 Trackbacks

Re: Common Applications

$MathML-enabled post (click for more details).$

Interesting observartions.

A tiny comment:

I think everybody will agree that the general pattern of statistical mechanics is indeed about more about inference than about nature per se. But at some point you want to apply all this to a particular case. Usually this amounts to specifying a Hamiltonian function.

And the precise details of that function is what encodes information about nature.

So there is a bit of information about nature - encoded in a Hamiltonian - and then there are means to extract certain parts of that information (entropy maximization, etc.).

Interestingly, while quantum mechanics is in a way nothing but statistical mechanics analytically continued to the complex plane, we usually tend to regard not just the Hamiltonian in quantum mechanics as encoding information about nature, but also the rest of the formalism.

Whether that “rest of the formalism” is really just a manifestation of our thinking or a genuine aspect of nature is hotly debated in all those discussions concerning the “interpretation of quantum mechanics”.

Posted by: urs on December 21, 2006 4:09 PM | Permalink | Reply to this

Re: Common Applications

I mentioned Christopher Fuchs, who thinks much of the apparatus of quantum mechanics is about information, here.

…it turns out to be rather easy to think of quantum collapse as a noncommutative variant of Bayes’ rule.

If I recall, he made the cut where you mention, at the Hamiltonian.

Posted by: David Corfield on December 21, 2006 4:25 PM | Permalink | Reply to this

Re: Common Applications

$MathML-enabled post (click for more details).$

I mentioned Christopher Fuchs, who thinks much of the apparatus of quantum mechanics is about information, here.

…it turns out to be rather easy to think of quantum collapse as a noncommutative variant of Bayes’ rule.

I tried to look at that paper and extract the gist of this statement.

The argument goes like this:

Starting with a density matrix $\rho$ the “state change” after finding the system in a state sitting in the image of the projector

(1)

E_d

is any of the density matrices

(2)

\rho_d = \frac{1}{P(d)} A_d \;\rho \; A_d^\dagger \,,

where the $A_d$ have to square to $E_d$

(3)

E_d = A_d^\dagger A_d

and are otherwise arbitrary.

That’s the simplified version (73) of the original equation (63) which is taken from reference [50].

Then, on p. 33 Fuchs notices that there are operators

(4)

\tilde \rho_d

that are unitarily equivalent to $\rho_d$ and such that

(5)

\rho = \sum_d \frac{1}{P(d)}\tilde \rho_d \,.

He concludes in the text around eqs. (93)-(95) that hence Bayes’ rule (70)

(6)

P(h) = \sum_d P(d)P(h|d)

has a quantum analog in that we have the operator equation

(7)

\rho = \sum_d P(d) V_d^\dagger \;\rho_d \; V_d

for some unitary operator $V_d$ .

Fuchs calls that a “noncommutative version” of Bayes’ rule.

I wonder if it might help if we instead say that this is Bayes’ equation holding up to specified isomorphism.

Posted by: urs on December 22, 2006 10:59 AM | Permalink | Reply to this

Re: Common Applications

$MathML-enabled post (click for more details).$

Bayes’ equation holding up to specified isomorphism.

Could you expand on that? Are you thinking of a categorification? Why do the $P$ s get treated differently, where the probability $P(d)$ reappears, but $P(h)$ is replaced by an operator?

Posted by: David Corfield on January 2, 2007 11:22 AM | Permalink | Reply to this

Re: Common Applications

$MathML-enabled post (click for more details).$

Bayes’ equation holding up to specified isomorphism.

Could you expand on that?

That’s a question I asked myself, too, when writing that comment! :-)

For the moment, the above is just a summary of Fuchs’s argument concerning the quantum version of Bayes’ rule and an observation concerning the nature of that rule.

Whether or not that argument together with that observation should be telling me something I have not decided yet.

Are you thinking of a categorification?

Well, that would be the obvious consequence after making that remark that I made. But I am not sure yet I can put all this into a coherent picture.

All I can observe is this:

Fuchs argues that we should take Bayes’ equation and do two things with it:

1) replace conditional probabilities - which are numbers - by partial density matrices $\rho_d$ , which are operators (read: morphisms).

2) replace these operators, in turn, by isomorphic operators $V_d^\dagger \rho_d V_d$ .

Why do the $P$ s get treated differently, where the probability $P(d)$ reappears, but $P(h)$ is replaced by an operator?

If one thinks that there is a deeper meaning hidden behind Fuchs’ observation, then these questions would need to be answered.

I cannot answer these questions yet. But I’ll try to think about it.

If it should really turn out to be true that there is a way to think of quantization as a categorification process, then it might be easier to go the other way around: try to understand in which sense passing to the classical limit of a quantum system can be understood as decategorification. But maybe John answered that already in your discussion about “changing the rig”?

I am not really sure about all this yet. I used to think of categorification and quantization as being orthogonal:

But quite possibly categorification can come to us in different guises here. I don’t know.

Posted by: urs on January 2, 2007 12:42 PM | Permalink | Reply to this

Re: Common Applications

$MathML-enabled post (click for more details).$

maybe John answered that already in your discussion about changing the rig

Well there John mentioned one-parameter deformations of classical statics into statistical mechanics, and, if we allow complex numbers, to quantum mechanics. The rig being deformed was $R_{max}$ = ( $R$ $\union$ { $+\infty$ }, min, +, $+\infty$ , 0). So it seemed to be rig replacement rather then categorification at stake.

How does this fit in with what Kapranov says on p. 2 of Noncommutative Geometry and Path Integrals:

the natural homomorphism $R \to R_{ab}$ of a noncommutative ring to its maximal commutative quotient is the algebraic analog of path integration,

The $R$ there is often a polynomial algebra over $\mathbb{C}$ . Passing to the quotient allows us to sum contributions from paths with the same endpoints, e.g., by allowing us to sum the contribution of a path in a lattice which goes East then North, with one which goes North then East. Presumably we can have polynomial algebras over $R_{max}$ , and say something similar. Instead of a noncommutative Fourier transform, this should lead to a noncommutative Legendre transform.

Posted by: David Corfield on January 2, 2007 2:44 PM | Permalink | Reply to this

Kapranov on path integrals

$MathML-enabled post (click for more details).$

How does this fit in with what Kapranov says on p. 2 of Noncommutative Geometry and Path Integrals:

the natural homomorphism $R \to R_{ab}$ of a noncommutative ring to its maximal commutative quotient is the algebraic analog of path integration,

Proposition 2.1.9 in this text says, in words (my paraphrase), the following:

parallel transport of a constant 1-form along a path $\gamma$ with values in a free group depends, when we pass to the corresponding free abelian group, only on the endpoint of the path.

As the author remarks, this is obvious. It means just slightly more that that the integral of a constant 1-form with values in the real numbers only depends on the endpoints (by Stokes theorem, if you like, since a constant 1-form is a closed 1-form).

In symbols this is written as

(1)

c(E_\gamma(Z)) = e^{(a,z)}

(p.7), where $E$ denotes the parallel transport $a$ the endpoint of the path $\gamma$ and $c$ the homomorphism from the free structure to the free abelian structure.

Now the argument is as follows:

integration over all paths from the origin to $a$ of this parallel transport (with constant 1 form $A$ !!) produces, for each endpoint $a$ , the sum (weighted by the chosen measure on the space of paths) of all possible ways to order the factors in the monomial

(2)

E_\gamma(Z) = \mathrm{lim}_{N = 1/\epsilon\to \infty} (e^{\epsilon A(\gamma'(0))}) (e^{\epsilon A(\gamma'(\epsilon))}) (e^{\epsilon A(\gamma'(2\epsilon))}) \cdots (e^{\epsilon A(\gamma'(a))}) \,.

In this way this path integral is like a projection of every monomial on its complete symmetrization.

Like, in the finite case:

(3)

XY \mapsto XY + YX

and

(4)

XYZ \mapsto XYZ + XZY + YXZ + YZX + ZXY + ZYX

and so on.

I’d need to further read this text to figure out which concrete profit is obtained from this observation.

For instance: say I have a non-constant 1-form on $\mathbb{R}^n$ with values in some Lie algebra.

The path integral over the corresponding parallel transport with the usual Wiener measure on paths can be made precise by using an generalization of the old Feynman-Kac formula.

The result is that the path integral over paths of length $t$ is the integral kernel of the operator

(5)

U(t) = \exp(it \nabla^\dagger \nabla) \,,

where

(6)

\nabla : H \to H

is the covariant derivative acting with respect to the given connection 1-form acting on square integrable sections of the (trivial, in this case) vector bundle over $\mathbb{R}^n$ .

I wonder: would the above observation on how the path integral of a constant 1-form projects onto a maximal commutative quotient allow us to rederive that formula from this point of view?

I don’t quite see how it would…

Posted by: urs on January 2, 2007 4:01 PM | Permalink | Reply to this

Re: Kapranov on path integrals

This caught my eye and gave a sense of deja vu :)

Posted by: Eric on January 2, 2007 7:43 PM | Permalink | Reply to this

Re: Common Applications

In connection with Fuchs’ viewpoint, see this discussion by Ray Streater, entitled “Locality in the EPR experiment”. It starts this way:

I. The von Neumann collapse postulate
In this section, we show that the postulate of von Neumann, that on measurement the wave function collapses to an eigenstate of the observable being measured, follows from Bayes’s rule for conditioning probabilities in classical probability.

Posted by: Chris Weed on December 29, 2006 6:12 PM | Permalink | Reply to this

Re: Common Applications

And Streater is a fan of Amari’s Information Geometry, treated by Caticha.

Posted by: David Corfield on January 2, 2007 11:02 AM | Permalink | Reply to this

Re: Common Applications

See the following, which cites Caticha’s paper:

Thomas Marlow, Relationalism vs. Bayesianism

Posted by: Chris Weed on December 30, 2006 12:07 AM | Permalink | Reply to this

Re: Common Applications

I love this discussion. It always brings me joy to see someone mention Jaynes as well :)

I’m now thinking about this stuff from a completely different perspective, i.e. finance and economics, but I think similar arguments carry over (as unobvious as that may sound). Jaynes similarly applied his ideas to economics. I think he was a visionary and will someday be recognized as such by a larger audience. I only wish I had stumbled onto his work earlier so that I might have met him.

Best regards,
Eric

Posted by: Eric on January 2, 2007 8:03 PM | Permalink | Reply to this

Re: Common Applications

In connection with the application of constructions of mathematical physics to machine learning, as well as Bayesianism, I thought some recent work of Shalizi and Crutchfield should be mentioned:

Pattern Discovery and Computational Mechanics

Computational mechanics is a method for discovering, describing and quantifying patterns, using tools from statistical physics. It constructs optimal, minimal models of stochastic processes and their underlying causal structures. These models tell us about the intrinsic computation embedded within a process—how it stores and transforms information. Here we summarize the mathematics of computational mechanics, especially recent optimality and uniqueness results. We also expound the principles and motivations underlying computational mechanics, emphasizing its connections to the minimum description length principle, PAC theory, and other aspects of machine learning.

Shalizi’s views on Bayesian approaches (to use a crude cover term) are interesting; I think he can be fairly described as a skeptic, as indicated here, here, and here (Pet peeves: Physicists who do not distinguish between a random variable (“X = the roll of a die”) and the value it takes (“x=5”). People who report numbers without error-bars or confidence-intervals. Bayesians.)

Posted by: Chris Weed on January 5, 2007 1:13 AM | Permalink | Reply to this

Read the post Ubiquitous Duality
Weblog: The n-Category Café
Excerpt: I'm in one of those phases where everywhere I look I see the same thing. It's Fourier duality and its cousins, a family which crops up here with amazing regularity. Back in August, John wrote: So, amazingly enough, Fourier duality...
Tracked: January 11, 2007 2:18 PM

Re: Common Applications

A discussion of complexity by Murray Gell-Mann, summarizing material in his book The Quark and the Jaguar, echoes the connections made in this post. Note in particular the emphasis on the relevance of a particular notion of regularities in this excerpt:

A measure that corresponds much better to what is usually meant by complexity in ordinary conversation, as well as in scientific discourse, refers not to the length of the most concise description of an entity (which is roughly what AIC is), but to the length of a concise description of a set of the entity’s regularities. Thus something almost entirely random, with practically no regularities, would have effective complexity near zero. So would something completely regular, such as a bit string consisting entirely of zeroes. Effective complexity can be high only a region intermediate between total order and complete disorder.

There can exist no procedure for finding the set of all regularities of an entity. But classes of regularities can be identified. Finding regularities typically refers to taking the available data about the entity, processing it in some manner into, say, a bit string, and then dividing that string into parts in a particular way and looking for mutual AIC among the parts. If a string is divided into two parts, for example, the mutual AIC can be taken to be the sum of the AIC’s of the parts minus the AIC of the whole. An amount of mutual algorithmic information content above a certain threshold can be considered diagnostic of a regularity. Given the identified regularities, the corresponding effective complexity is the AIC of a description of those regularities.

More precisely, any particular regularities may be regarded as embedding the entity in question in a set of entities sharing the regularities and differing only in other respects. In general, the regularities associate a probability with each entity in the set. (The probabilities are in many cases all equal but they may differ from one member of the set to another.) The effective complexity of the regularities can then be defined as the AIC of the description of the set of entities and their probabilities. (Specifying a given entity, such as the original one, requires additional information.)

I can’t resist quoting from another of Gell-Mann’s essays posted at SFI, entitled “Nature Conformable To Herself”, which is highly relevant to the topic of David’s post:

To answer those questions, we need to deal first with the widespread notion that all scientific theory is nothing but a set of constructs with which the human mind attempts to grasp reality, a notion associated with the German philosopher Immanuel Kant. Although I had heard of that belief many times, I first came into collision with it thirty-six years ago in Paris.

At that time, I was a visiting professor at the Collège de France, founded by Francis I more than four hundred years earlier. (As far as I know, I was the first visiting professor in the history of that venerable institution.) My office was in the laboratory of experimental physics established by Francis Perrin, a well-known scientist who was a permanent professor at the Collège. On visits to the offices of the junior experimentalists down the hall, I noticed that they spent a certain amount of time drawing little pictures in their notebooks, which I assumed at first must be diagrams of experimental apparatus. Many of the drawings turned out, however, to be sketches of a gallows for hanging the vice-director of the lab, whose rigid ideas drove them crazy.

I soon got to know the sous-directeur, and we conversed on various subjects, one of which was Project Ozma, an early attempt to detect possible signals from other technical civilizations on planets orbiting nearby stars. The corresponding project nowadays is called the Search for Extraterrestrial Intelligence. We discussed how communication might take place if alien intelligences broadcasting signals were close enough to the solar system, assuming that both interlocutors would have the patience to wait years for the signals to be transmitted back and forth. I suggested that we might try beep, beep-beep, beep-beep-beep, etc. to indicate the numbers 1, 2, 3, and so forth, and then perhaps 1, 2, 3,…42, 44…..60, 62…….92, for the atomic numbers of the 90 chemical elements that are stable—1 to 92 except for 43 and 61. “Wait,” said the sous-directeur, “that is absurd. Those numbers up to 92 would mean nothing to such aliens…. Why, if they have 90 stable chemical elements as we do, then they must also have the Eiffel Tower and Brigitte Bardot.”

That is how I became acquainted with the fact that French schools taught a kind of neo-Kantian philosophy, according to which the laws of nature are nothing but Kantian “categories” used by the human mind to describe reality.

Posted by: Chris Weed on January 13, 2007 2:00 AM | Permalink | Reply to this

Pomo (Was: Common Applications)

Chris Weed qouted Murray Gell-Mann, quoting a sous-directeur:

“Why, if they have 90 stable chemical elements as we do, then they must also have the Eiffel Tower and Brigitte Bardot.”

That is how I became acquainted with the fact that French schools taught a kind of neo-Kantian philosophy, according to which the laws of nature are nothing but Kantian “categories” used by the human mind to describe reality.

Well, that is just stupid of the sous-directeur.

I see nothing wrong with the idea, as phrased above, that

all scientific theory is nothing but a set of constructs with which the human mind attempts to grasp reality[.]

Indeed, it seems obviously correct to me, (although there are probably other good ways of looking at it). But the sous-directeur is not applying this philosophy consistently. He seems to think that there are minds (his, Gell-Mann’s, other humans’, and even aliens’) first, and then these various minds come up with ideas to describe reality. Certainly something like this is going on, but he has forgotten that the aliens are also part of reality (our reality, as we describe it, at least under the hypothesis that we find some). If, as in the scenario that Gell-Mann introduced, they are close enough that we can communicate back and forth in our lifetimes, then our understanding of science indicates that they have the same stable nuclear isotopes available.

If you doubt that science, then very well, but what is the basis for believing in the process of communiciation, or even the aliens’ existence? He may as well say “I cannot discuss the Eiffel Tower with you, Dr. Gell-Mann; for if you know about that, then you must also know all my secret inner thoughts, which is absurd.” On the contrary, the same science (subjective description of reality) that says that Gell-Mann can’t read the sous-directeur’s mind also says that Gell-Mann can see the Eiffel Tower (and exists in the first place); and the same subjective description of reality that would (in the hypothetical situation before us) say that the aliens haven’t built an Eiffel Tower also says that they have interacted with the 90 stable chemical elements.

There’s nothing wrong with these postmodernist critiques of naïve realism, but you’ve got to do it seriously. If you just do it half way (like applying a sort of Cartesian dualism, then saying that the material world is a subjective illusion but minds or souls have an absolute existence, which seems appallingly common among the scientifically illiterate), then you’re just going to get nonsense.

Actually, I take a very extreme view about communication with alien life forms, in that I don’t find it all obvious that they will even have pure mathematics like ours. (Forget numbering the chemical elements; can they even count?) It’s certainly a good place to start, especially if we have nothing else to talk about, but that’s because we don’t know any alternative. Still, it is possible to communicate with cultures that have no mathematics, if you have something else to discuss, and I wouldn’t be surprised if that’s how it happens first. Nevertheless, when I think about the aliens as features of reality, then I will use our science and mathematics, which may well be changed by our communication with them but will not go away.

Posted by: Toby Bartels on January 13, 2007 9:47 PM | Permalink | Reply to this

Read the post Aaronson on the Nature of Quantum Mechanics
Weblog: The n-Category Café
Excerpt: Scott Aaronson on the nature of quantum mechanics.
Tracked: January 16, 2007 3:04 PM

Read the post Category Theoretic Probability Theory
Weblog: The n-Category Café
Excerpt: Having noticed (e.g., here and here) that what I do in my day job (statistical learning theory) has much to do with my hobby (things discussed here), I ought to be thinking about probability theory in category theoretic terms....
Tracked: February 7, 2007 11:57 AM

The n-Category Café

Skip to the Main Content

December 21, 2006