June 29, 2020
Getting to the Bottom of Noether’s Theorem
Posted by John Baez
Most of us have been staying holed up at home lately. I spent the last month holed up writing a paper that expands on my talk at a conference honoring the centennial of Noether’s 1918 paper on symmetries and conservation laws. This made my confinement a lot more bearable. It was good getting back to this sort of mathematical physics after a long time spent on applied category theory. It turns out I really missed it.
While everyone at the conference kept emphasizing that Noether’s 1918 paper had two big theorems in it, my paper is just about the easy one—the one physicists call Noether’s theorem:
June 27, 2020
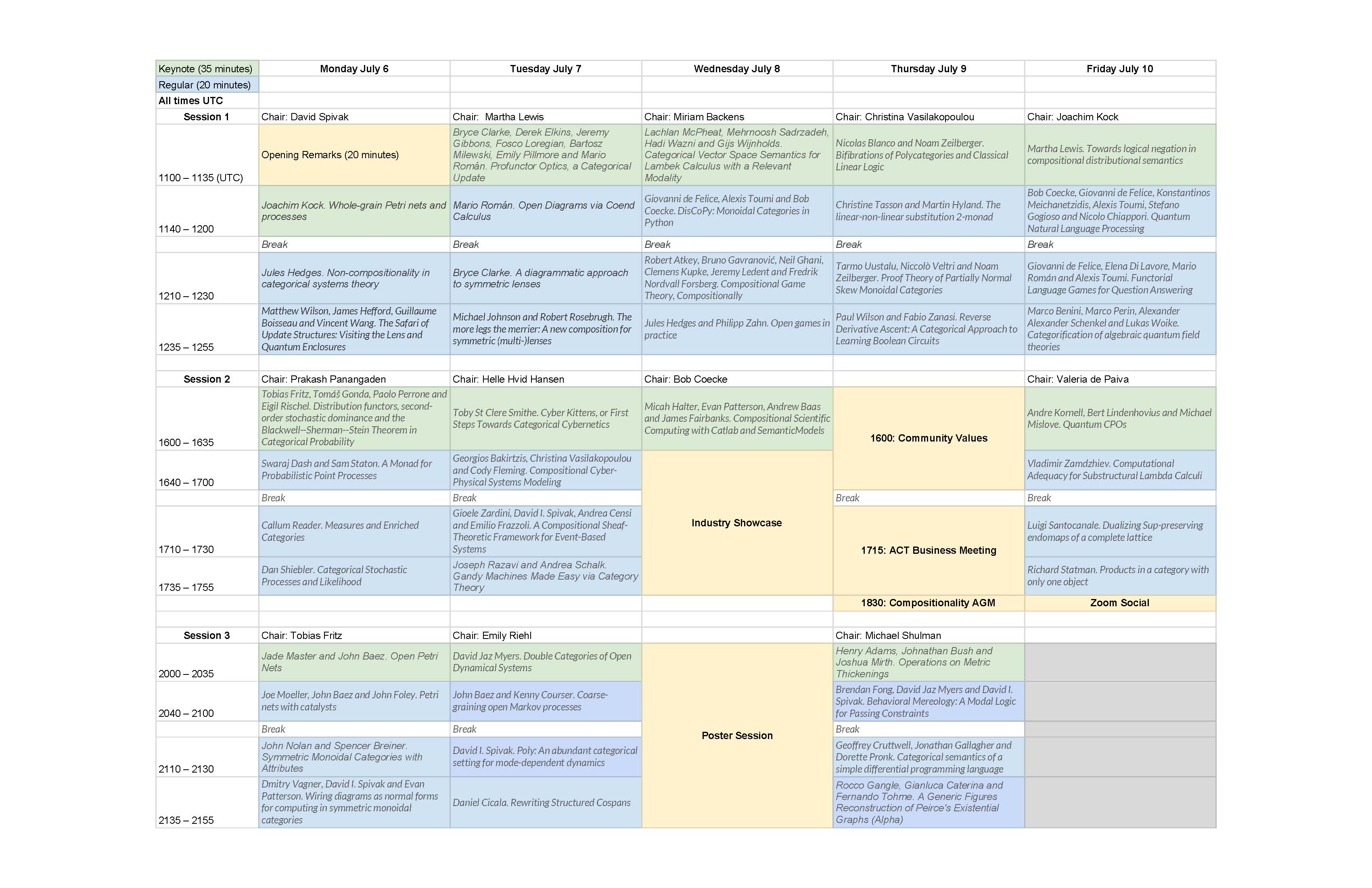
ACT2020 Program
Posted by John Baez
Applied Category Theory 2020 is coming up soon! After the Tutorial Day on Sunday July 6th, there will be talks from Monday July 7th to Friday July 10th.
Here is the program—click on it to download a more readable version:
All talks will be live on Zoom. Recorded versions should appear on YouTube later.
And here’s a list of the talks….
June 17, 2020
ACT2020 Tutorial Day
Posted by John Baez
If you’re wanting to learn some applied category theory, register for the tutorials that are taking place on July 5, 2020 as part of ACT2020!
More details follow….
June 11, 2020
Categorical Statistics Group
Posted by John Baez
As a spinoff of the workshop Categorical Probability and Statistics, Oliver Shetler has organized a reading group on category theory applied to statistics. The first meeting is Saturday June 27th at 17:00 UTC.
You can sign up for the group here, and also read more about it there. We’re discussing the group on the Category Theory Community Server, so if you want to join the reading group should probably also join that.
June 7, 2020
Jordan Algebras
Posted by John Baez
I’ve learned a fair amount about Jordan algebras by now, but I still don’t have a clear conceptual understanding of the Jordan algebra axioms, and it’s time to fix that.
A Jordan algebra is a vector space with a commutative bilinear operation that obeys
That’s how Wikipedia defines it. This axiom is an affront to my mathematical sense of taste. It looks like a ridiculously restricted version of the associative law, plucked from dozens of variants one could imagine. There has to be a better way to understand what’s going on here!
June 1, 2020
Categorical Probability and Statistics 2020
Posted by Tom Leinster
Guest post by Tobias Fritz, Rory Lucyshyn-Wright, and Paolo Perrone
As many of you will already know, we are organizing the workshop Categorical Probability and Statistics, which will take place online over the upcoming weekend, June 5–8.
The goal is to provide a platform for exchange of results and ideas between the various communities who pursue categorical approaches to probability and statistics. The talks will be hosted on Zoom and accompanied by discussions in a chat forum. The final schedule of the talks is available under the link above.
 Posts with this logo use
Posts with this logo use