Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

December 25, 2007

Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

Hisham Sati, Jim Stasheff and myself are working on writing up some ideas on Lie $∞$ -algebra cohomology and its application to String- and Chern-Simons $n$ -Transport, further exploring the second edge of the cube.

We would like to share this document:

H. Sati, J. Stasheff, U. S.
$L_{∞}$ -algebra connections and applications to String- and Chern-Simons $n$ -Transport
arXiv:http://arxiv.org/abs/0801.3480
(pdf of the latest version)

This consists of three parts:

Part A : Overview and physical applications
Part B: Lie $∞$ -algebras, their cohomology and their String-like extensions
Part C: Categorified Cartan-Ehresmann connections and lifts through String-like extensions.

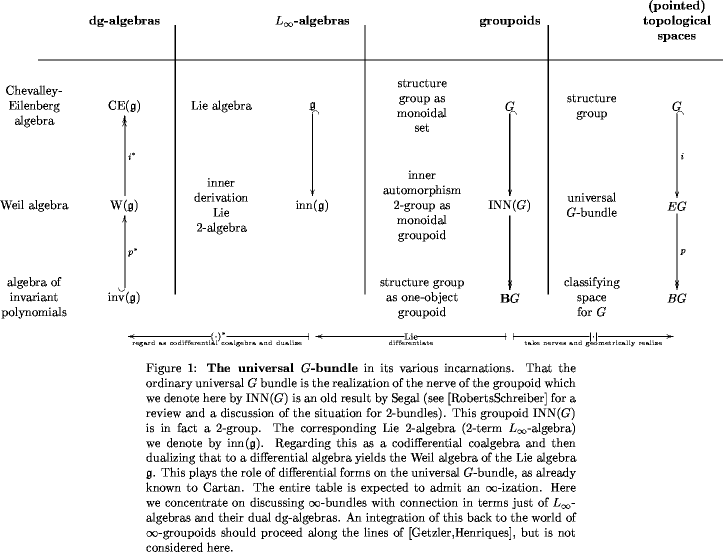
This can be thought of as providing details to the discussion provided in my slide show String- and Chern-Simons $n$ -Transport. $N$ -Café regulars will recognize a certain synthesis of topics I used to discuss here, like inner automorphism $n + 1$ -groups, String and Chern-Simons Lie $∞$ -algebras, $n$ -Curvature , obstruction theory and other things. To some extent, the main idea here found its final form after John posed a nice problem in Higher Gauge Theory and Elliptic Cohomology.

Much progress on the relation of the general formalism to (heterotic) string theory and supergravity/M-theory occurred when I visited Hisham Sati in Yale. The full implications are only briefly indicated here.

We’d be grateful for whatever comment you might have.

$MathML-enabled post (click for more details).$

Math abstract. We give a generalization of the notion of a Cartan-Ehresmann connection from Lie algebras to $L_{∞}$ -algebras and use it to study the obstruction theory of lifts through higher String-like extensions of Lie algebras.

Physics abstract. It is known that over a D-brane the Kalb-Ramond field restricts to a 2-bundle with connection (a gerbe) which can be seen as the obstruction to lifting the $PU (H)$ -bundle on the D-brane to a $U (H)$ -bundle. We discuss how this phenomenon generalizes from the ordinary central extension $U (1) \to U (H) \to PU (H)$ to higher categorical central extensions, like the String-extension $B U (1) \to String (G) \to G$ . Here the obstruction to the lift is a 3-bundle with connection (a 2-gerbe): the Chern-Simons 3-bundle classified by the first Pontrjagin class. For $G = Spin (n)$ this obstructs the existence of a String-structure. We discuss how to describe this obstruction problem in terms of Lie $n$ -algebras and their corresponding categorified Cartan-Ehresmann connections. Generalizations even beyond String-extensions are then straightforward. For $G = Spin (n)$ the next step is “Fivebrane structures” whose existence is obstructed by certain generalized Chern-Simons 7-bundles classified by the second Pontrjagin class.

Statement of the main results

We define, for any $L_{∞}$ -algebra $g$ and any smooth space $X$ , a notion of

$•$ $g$ -descent objects over $X$ ;

and an extension of these to

$•$ $g$ -connection descent objects over $X$ .

These descent objects are to be thought of as the data obtained from locally trivializing an $n$ -bundle (with connection) whose structure $n$ -group has the Lie $n$ -algebra $g$ .

We define for each $L_{∞}$ -algebra $g$ a dg-algebra $inv (g)$ of invariant polynomials on $g$ .

We show that every $g$ -connection descent object gives rise to a collection of deRham classes on $X$ : its characteristic classes. These are images of the cohomology of $inv (g)$ .

Two descent objects are taken to be equivalent if they are concordant in a natural sense.

Our first main result is

Theorem. Characteristic classes indeed characterize $g$ -descent objects in the following sense:

- Concordant $g$ -connection descent objects agree in cohomology and have the same characteristic classes.

- Two $g$ -descent objects with the same characteristic classes agree in cohomology.

- If two $g$ -descent objects differ in cohomology, they are not concordant and cannot have the same characteristic classes.

Remark. We expect that this result can be strengthened. Currently our characteristic classes are just in deRham cohomology. One would expect that these are images of classes in integral cohomology which completely characterize equivalent $g$ -descent objects. While we do not attempt here to discuss integral characteristic classes in general, we discuss some aspects of this for the case of abelian Lie $n$ -algebra $g = b^{n - 1} u (1)$ by relating $g$ -descent objects to Deligne cohomology.

We define String-like extensions $g_{μ}$ of $L_{∞}$ -algebras coming from any $L_{∞}$ -algebra cocycle $μ$ : a closed element in the Chevalley-Eilenberg dg-algebra corresponding to $g$ : $μ \in CE (g)$ . These generalize the String Lie 2-algebra which governs the dynamics of (heterotic) superstrings.

Then we do this and that and arrive at our second main result:

Theorem. For $μ \in CE (g)$ any degree $n + 1$ $g$ -cocycle that transgresses via $cs \in W (g)$ to an invariant polynomial $P \in inv (g)$ , the obstruction to lifting a $g$ -descent object to a $g_{μ}$ -descent object is a $(b^{n} u (1))$ -descent object whose single characteristic class is the class corresponding to $P$ of the original $g$ -descent object.

We discuss the following applications.

- For $g$ an ordinary semisimple Lie algebra and $μ$ its canonical 3-cocycle, this says the obstruction to lifting a $g$ -bundle to a String 2-bundle is a Chern-Simons 3-bundle. The vanishing of this obstruction is known as a String structure.

- This result generalizes to all String-like extensions. Using the 7-cocycle on $so (n)$ we obtain lifts through extensions by a Lie 6-algebra, which we call the Fivebrane Lie 6-algebra. Accordingly, fivebrane structures are obstructed by the second Pontrjagin class and are related to higher twists in string theory.

- This pattern continues and one would expect our obstruction theory for lifts through string-like extensions with respect to the 11-cocycle on $so (n)$ to correspond to Ninebrane structure.

The issue of $p$ -brane structures for higher $p$ was discussed before in [MickelssonPercacci]. In contrast to the discussion there, we here see $p$ -brane structures only for $p = 4 n + 1$ , corresponding to the list of invariant polynomials and cocycles for $so (n)$ .

- We discuss how the action functional of the topological field theory known as BF-theory arises from the invariant polynomial on a strict Lie 2-algebra, in a generalization of the integrated Pontrjagin 4-form of the topological term in Yang-Mills theory.

This is similar to but different from the Lie 2-algebraic interpretation of BF theory indicated in [GirelliPfeifferPopescu], where the “cosmological” bilinear in the connection 2-form is not considered and a constraint on the admissable strict Lie 2-algebras is imposed.

- We discuss the parallel transport induced by a $g$ -connection, relate it to the $n$ -functorial parallel transport and point out how this leads to $σ$ -model actions in terms of dg-algebra morphisms. This makes contact with the corresponding BV-formalism, though the details of that are not discussed here.

Posted at December 25, 2007 5:55 PM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1549

33 Comments & 19 Trackbacks

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Does this work tell us anything about all those dualities (S, T, U, etc.) between string theories?

Posted by: David Corfield on December 26, 2007 10:09 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

When ordinary Lie algebras are enough, do we see these dualities in those terms?

Posted by: jim stasheff on December 26, 2007 2:03 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Jim Stasheff asked:

When ordinary Lie algebras are enough, do we see these [string] dualities in those terms?

Ulrich Bunke and collaborators claim to have made precise the heuristic statement that topological T-duality is Pontrjagin-duality generalized from ordinary groups to $n$ -groups.

See my very brief discussion here.

This looks like a result which would open the way to understanding (topological) T-duality much more generally, not just for line 2-bundles (1-gerbes) but for line $n$ -bundles for all $n$ , including $n = 1$ .

Maybe something to keep in mind.

Posted by: Urs Schreiber on December 27, 2007 2:43 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Does Bunke have a pre-pre-print yet?
dopes he have e-mail?

jim

Posted by: jim stasheff on December 27, 2007 5:21 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Does Bunke have a pre-pre-print yet?

Yes, here:

Bunke, Schick, Spitzweck, Thom: Duality for topological abelian group stacks and T-duality

Posted by: Urs Schreiber on December 27, 2007 9:12 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Perhaps I’m just after Urs giving us a glimpse of what might interest the string theorist in his work if everything pans out as he hopes.

Posted by: David Corfield on December 26, 2007 4:41 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Perhaps I’m just after Urs giving us a glimpse of what might interest the string theorist in his work if everything pans out as he hopes.

Apart from the aspects I mentioned in a previous reply the main application to string theory which we announce and indicate in Part A is the understanding of background structures that generalize ordinary Spin-structures.

From the physical point of view, a Spin structure on a manifold is the necessary prerequisite to have a consistent theory of spinning particles (= 1-particles) on this manifold.

In superstring theory one studies spinning $n$ -particles (aka $(n - 1)$ -branes) for larger $n$ .

It is pretty well known that the structure generalizing a Spin structure as we move from 1-particles to 2-particles is what is called String structure.

These String-structures have originally been understood (by Killingback and later Witten, nicely explained byMurray-Stevenson) in terms of bundles on the loop space of the underlying manifold. Then it was understood that this really corresponds to a 2-bundle down on the manifold itself.

This observation our work here describes further and generalizes to higher $n$ .

There are spinning 5-branes, and they should have a consistent quantization only on manifolds which have a “Fivebrane structure”, which in turn should be the requirement that a certain 6-bundle exists on that manifold.

We provide the language to talk about these 6-bundles. And about the 10-bundles which should give “Ninebrane structures”. We show that – whichever role they actually play physically – the existence of these structures is obstructed by higher Pontrjagin classes.

This is not too surprising once you understand the pattern governing ordinary String structures. But it is good to have a solid understanding of it.

There is much more to say about Fivebrane structures. But this is supposed to be the topic of a separate article.

Posted by: Urs Schreiber on December 27, 2007 3:10 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

David Corfield asked:

Does this work tell us anything about all those dualities (S, T, U, etc.) between string theories?

Well, not yet directly. But it is a necessary prerequisite of some other work which should build on it and have more concrete things to say about autoequivalences of the 2- and the 3-particle, otherwise known as string dualities.

I wish progress were as quick as the open questions are clear and urgent!

The best understood duality is T-duality, which is an autoequivalence on structures that involve a Riemannian structure and a $b u (1)$ -2-bundle, aka an abelian gerbe. The description of its aspect which relies only on the gerbe, known as topological T-duality is finding its $n$ -categorical formulation (slightly secretly, still) in the theory of bi-branes. The powerful description in terms of generalized complex geometry I had indicated how to incorporate in the $n$ -categorical picture in The $G$ and the $B$ .

One important point one would want is a better understanding of the relation of $b u (1)$ -2-bundles and their T-duality properties on a dimensionally compactified space to the $b^{2} u (1)$ -3-bundles and their properties on the uncompactified space which they come from. This is known as the problem of S-duality invariance of twisted K-theory.

The problem is that under dimensional compactification, the $b^{2} u (1)$ -3-bundle reduces to a $b u (1)$ -2-bundle (the “Kalb-Ramond field”) plus lots of “other stuff”, known as RR-fields. There is to date no good global description of RR-fields as there is for the Kalb-Ramond field. Since they all come from the $b^{2} u (1)$ -3-bundle upstairs (the “ $C$ -field”) a good strategy seems to be to better study this 3-bundle.

What the results presented here apply most directly to is the clarification of the global $n$ -bundle interpretation of these string background “fields”, notably the supergravity $C$ -field just mentioned.

The currently best available description of the “ $C$ -field”, mentioned above, in the string theory literature seems to be that given by Diaconescu, Freed, Moore, whose Deligne-cohomological interpretation was worked out more clearly by Clingher.

I think it is fair to say that this leaves room for improvement. As we indicate (but don’t discuss in full detail), the $C$ -field should be the Chern-Simons 3-bundle with connection which obstructs the lift of a given $Spin (n) \times E_{8}$ 1-bundle to the corresponding String 2-bundle.

Form there on I would try to tackle further those dualities.

Posted by: Urs Schreiber on December 27, 2007 2:22 PM | Permalink | Reply to this

universal g-connection

$MathML-enabled post (click for more details).$

In the context of the above, I’d like to look again at the question we were discussing here in the thread “On BV Quantization, Part VIII”, about whether and how bundles with connection can be classified by maps of “spaces”.

To some degree, the developments in Part B indicate an answer to that.

To see that, one should notice that graded-commutative differential algebras (dg-algebras for short, in the following) are pretty close to being spaces. I’ll say something about that now. With that in mind, everything we say about bundles with connections in terms of dg-algebras can be translated into a description in terms of spaces.

It’s essentially the idea of rational homotopy theory: whenever you see a graded-commutative dg-algebra, you can think of it as being the dg-algebra of differential forms on some space.

But I’ll slightly vary the theme of rational homotopy theory (or rather, of what I know about it) here and instead of relating simplicial spaces to dg-algebras, relate them to smooth spaces in the sense of sheaves on manifolds.

So for me now, a smooth space is a sheaf on a site $S$ , which might be open (convex) subsets of $ℝ \cup ℝ^{2} \cup ℝ^{3} \cup \dots$ , or might be the site of all manifolds, or some other site on whose objects we naturally have smooth differential forms.

I write $S^{∞} : = Sh (S)$ for the category of smooth spaces in this sense.

There is a natural notion of differental forms on such a smooth space:

differential forms themeselves form a smooth space, given by the sheaf that sends each manifold $U$ to the set of differential forms on it: $Ω^{•} : U \mapsto Ω^{•} (U) .$

Given any other sheaf $X \in Sh (S)$ , a differential form $ω$ on $X$ is a morphisms (of sheaves)

$ω : X \to Ω^{•} .$

Here you should think for each object $U$ of our site of each element in the set $X (U)$ as a smooth map $f$ from $U$ into $X$ , and of the image $ω_{U} (f)$ of that element under $ω_{U}$ as the differential form $f^{*} ω$ on $U$ obtained by pullback along that map $f$ of a differential form $ω$ on $X$ .

The set of all differential forms on $X$ is hence

$Ω^{•} (X) : = {Hom}_{S^{∞}} (X, Ω^{•}) .$

One checks easily that this inherits the structure of a graded-commutative dg-algebra from the fact that $Ω^{•} (U)$ is a commutative dg-algebra for all $U$ and that exterior derivative and wedge product commute with pullbacks.

This gives us a contravariant functor from smooth spaces to graded-commutative dg-algebras:

$Ω^{•} : S^{∞} \to DGCA .$

There is another functor going the other way:

given any differential graded-commutative algebra, which I’ll write $CE (g, V)$ , we obtain a smooth space $X_{g, V}$ by setting

$X_{g, V} : U \mapsto {Hom}_{dg - Alg} (CE (g, V), Ω^{•} (U)) .$

(This is the basic idea underlying Sullivan models in rational homotopy theory.)

This yields a contravariant functor $S^{∞} \leftarrow DGCA : {Hom}_{dg - Alg} (- -, Ω^{•} (- -)) .$

I am not sure right now in full generality to which extent these two functors are mutual inverses or adjoints. But they should be.

One thing that is directly clear is that every graded-commutative algebra $CE (g, V)$ sits at least inside the algebra of differential forms $Ω^{•} (X_{g, V})$ on the space $X_{g, V}$ it defines:

$CE (g, V) ↪ Ω^{•} (X_{g, V}) .$

This is a tautology following from the way $X_{g, V}$ and $Ω^{•} (X)$ were defined.

But for instance I think one easily checks that $Ω^{•} (X) = Ω^{•} (X_{Ω^{•} (X)}),$ which is reassuring.

Now, take our article and hit everything in sight with the functor $S^{∞} \leftarrow DGCA : {Hom}_{dg - Alg} (- -, Ω^{•} (- -))$ thus sending our discussion in terms of DGCAs entirely to a discussion in terms of smooth spaces.

This then yields, in particular, the following statements:

for every Lie $∞$ -algebra $g$ there is a smooth space $X_{inn (g)}$ such that $g$ -valued forms $A$ on any smooth space $Y$ correspond to smooth maps $f_{A} : Y \to X_{inn (g)} .$

The “ $g$ -connection descent objects” on a space $X$ which we describe, and which encode $n$ -bundles with connection with values in $g$ are characterized by maps of smooth spaces $X \to X_{inv (g)}$ with the property that we can complete the two squares in $\begin{matrix} F & \to & X_{g} \\ ↓ & ↓ \\ Y & \to & X_{inn (g)} \\ ↓ & ↓ \\ X & \to & X_{inv (g)} \end{matrix} .$

The horizontal morphism at the bottom here plays the role of the classifying map as familiar from ordinary bundles. Indeed, for $g$ an ordinary Lie algebra, $X_{inv (g)}$ is a smooth space with the same deRham cohomology as (any smooth model of) $B G$ .

Then the fact that a surjective submersion $\begin{matrix} Y \\ ↓ \\ X \end{matrix}$ appears is the phenomenon that John likes to refer to in terms of anafunctors. The smooth map $Y \to X_{inn (g)}$ which covers our classifying map $X \to X_{inv} (g)$ is the one that actually encodes the connection in detail, whereas $Y \to X_{inv (g)}$ only knows about the characteristic forms of the conneciton form(s).

So, we don’t see here, directly, a single smooth space such that smooth maps into it classify bundles with connection.

Rather, we see a smooth space $X_{inv (g)}$ characterizing bundles and being covered by another smooth space, $X_{inn (g)}$ , maps into which characterize connections on a trivial bundle. Fit together into a diagram as above, these maps characterize (nontrivial) bundles with connections.

Despite of this, we can after all speak of a universal connection in this context, and that’s probably all we actually want.

I talked about that before (also at the end of the slide show), but let me say it again, with the above picture now more clearly present:

from what I just said, if follows that the space $X_{inv (g)}$ (which is essentially $B G$ ) supports not only a canonical $G$ -bundle $\begin{matrix} X_{inn (g)} \\ ↓ \\ X_{inv (g)} \end{matrix}$

but also that this universal bundle carries canonically a $g$ -connection: this is because we can canonically complete the identity morphism $Id : X_{inv (g)} X_{inv (g)}$ to a $g$ -connection descent object, simply by having identities on all horizontal edges: $\begin{matrix} X_{g} & \overset{Id}{\to} & X_{g} \\ ↓ & ↓ \\ X_{inn (g)} & \overset{Id}{\to} & X_{inn (g)} \\ ↓ & ↓ \\ X_{inv (g)} & \overset{Id}{\to} & X_{inv (g)} \end{matrix} .$

This is the universal $g$ -connection (descent object) on the unversal $g$ -bundle (descent object).

(But notice the remark from our introduction: right now we haven’t shown that the classification of these things by deRham classes lifts to integral classes. And also notice that what I am saying here would be fully satisfactory only when we know to which extent the two contravariant functors $Ω^{•} : S^{∞} \to DGCAs$ and $Hom (- -, Ω^{•} (- -)) : DGCAs \to S^{∞}$ are inverses of each other, at least for the DDCAs we are encountering here.)

And clearly, any other $g$ -connection (descent object) is the pullback of this universal one, simply in the tautological sense that every morphism is the pullback of the identity on its target along itself.

Posted by: Urs Schreiber on December 27, 2007 1:37 PM | Permalink | Reply to this

Re: universal g-connection

$MathML-enabled post (click for more details).$

Following up on my discussion of graded commutative differential algebras and smooth spaces, above, I am wondering if this can be used to understand the internal hom in the category of DGCAs.

That’s because smooth spaces, being sheaves, canonically have an internal hom. Therefore for $A$ and $B$ any two DGCAs, the DGCA corresponding to $hom (A, B)$ should e something like $Ω^{•} ({hom}_{Sheaves} (X_{B}, X_{A}))$ where $X_{A}$ and $X_{B}$ are the smooth spaces induced by $A$ and $B$ as described above.

I’d be grateful for all comments/help here. Jim?

Posted by: Urs Schreiber on December 27, 2007 3:43 PM | Permalink | Reply to this

Re: universal g-connection

You’d have to sheafify me first.
Todd??

Posted by: jim stasheff on December 27, 2007 5:22 PM | Permalink | Reply to this

Re: universal g-connection

$MathML-enabled post (click for more details).$

You’d have to sheafify me first.

What I can offer right this moment are some quickly typed

Notes on differential forms on smooth spaces and graded-commutative differential algebras.

Posted by: Urs Schreiber on December 27, 2007 9:19 PM | Permalink | Reply to this

Re: universal g-connection

$MathML-enabled post (click for more details).$

Hi Urs,

Took a look at your comment and notes; here are some initial reactions.

First, you asked whether the formula

U \mapsto hom (U \times X, Y)

gives the ‘correct’ internal hom for smooth spaces; in this context I assume you’re asking whether this gives the correct exponential for cartesian closedness.

Yes, this formula is correct and works for general presheaf toposes, by an application of the Yoneda lemma. The result is standard and proved in many books on topos theory – the ones by Johnstone, by Mac Lane and Moerdijk, and by Freyd and Scedrov come to mind. I’m happy to go into more detail if you want.

Second: there is as you say a contravariant adjunction

S^{∞} (X, DGCA (A, Ω^{•} (-))) ≅ DGCA (A, S^{∞} (X, Ω^{•} (-))) .

This can be proved with the help of (again) the Yoneda lemma: since $X$ is a colimit of representables, one can easily reduce to the case where $X$ is a representable, and then check that case with the help of Yoneda. Notice that this type of adjunction has the general flavor of one coming from a Janusian/ambimorphic object ( $Ω^{•} (-)$ having a kind of dual existence, one as a smooth space and another as a DGCA).

But, I don’t think this adjunction can be an equivalence, even if we restrict to locally quasi-free DGCA’s. The question seems to be whether ${DGCA}^{op}$ (or something like it) is equivalent to the topos $S^{∞}$ , and it’s sort of an interesting question because ${DGCA}^{op}$ does partake of some of the exactness properties satisfied by a topos. For one, it’s a lextensive category (it has finite pullbacks and finite coproducts which are disjoint and preserved under pullback) – lextensive categories are a very interesting and much-studied class of categories.

But I sort of doubt ${DGCA}^{op}$ or some easily identified full subcategory is locally cartesian closed (which it would be if it were a topos). This would mean that general colimits in this category are preserved under pulling back (one says “colimits are universal”), or that limits in $DGCA$ are preserved under pushing out. The pushout of a pair of morphisms

B \leftarrow A \to C

in $DGCA$ is given by $B \otimes_{A} C$ ; the question is whether $B \otimes_{A} -$ preserves limits of $A$ -modules. Preservation of equalizers may be no big deal under some condition like “locally quasi-free” (although there one would have to watch out that objects satisfying that condition give a complete and cocomplete category – I’m not so sure about that), but $B \otimes_{A} -$ preserving arbitrary products, not just finite ones, looks like a much taller order.

(Another exactness condition to check has to do with whether there is an exact correspondence between epimorphisms and equivalence relations: whether every epi is the quotient of its kernel pair, and whether every equivalence relation is the kernel pair of its quotient. Never mind that for now.)

This is pretty much a gut reaction, and I feel it will probably read like a wet blanket reaction as well, which I really don’t mean. It’s possible that the desiderata of ‘internal homs’ could be relaxed a bit to stop short of actual cartesian closedness and still be interesting, but I just don’t know off hand. (By the way, I wanted to get back to you some time on calculations of internal homs of differential graded cocommutative coalgebras, but my first two attempts were obliterated by my 3-year-old daughter, and somehow I haven’t found much time for math during this holiday season.)

I would very much like to follow up some time on what you’re saying about universal bundles with connections.

Posted by: Todd Trimble on December 30, 2007 3:44 PM | Permalink | Reply to this

Re: universal g-connection

$MathML-enabled post (click for more details).$

Todd,

this is a fantastically helpful reply. Really.

Instead of reacting here, I’ll move this entire discussion about smooth spaces versus DGCAs to a separate entry, in order to better do it justice, and not to clutter the comment section of this entry here with something that is not actually entirely on target.

The new entry is here: Transgresson of $n$ -Transport and $n$ -Connection

Posted by: Urs Schreiber on December 30, 2007 6:05 PM | Permalink | Reply to this

Re: universal g-connection

First partial response to Urs:

There is another functor going the other way:

given any differential graded-commutative algebra, which I’ll write CE(g,V), we obtain a smooth space X g,V by setting

I THINK YOU WANT QUASI-FREE DGCA

SEE ORIGINAL COMMENT OF URS FOR THE DESCRIPTION OF THE FUNCTOR

UNLESS YOU ALREADY HAVE A SPACE AND THIS IS TO DEFINE THE SMOOTHNESS, WHAT IS U?

(This is the basic idea underlying Sullivan models in rational homotopy theory.)

This yields a contravariant functor
S ∞←DGCA:Hom dg−Alg(−−,Ω •(−−)).

CONTRAVARIANT WITH REPSEC TO THE FIRST –
AND THE SECOND??

Posted by: jim stasheff on December 28, 2007 1:41 PM | Permalink | Reply to this

Re: universal g-connection

$MathML-enabled post (click for more details).$

Jim wrote:

I THINK YOU WANT QUASI-FREE DGCA

Well, I think I want something like locally quasi free. The dg-algebra of differential forms on a space is not in general quasi free. But when restricted to small enough patches it is.

Or put differently: quasi-free dg-algebras correspond to $∞$ -groupoids with just a single object. Here I need to allow mor general spaces of objects.

UNLESS YOU ALREADY HAVE A SPACE AND THIS IS TO DEFINE THE SMOOTHNESS, WHAT IS $U$ ?

$U$ is an object of the underlying site. So either an ordinary manifold, or an open (convex, maybe) subset of $ℝ \cup ℝ^{2} \cup ℝ^{3} \cup \dots$ , depending on taste and on the application.

My smooth spaces $X$ here are presheaves on ordinary manifolds/open subsets. To each ordinary manifold $U$ they assign a set, $X (U)$ which is to be thought of as the set of smooth maps from $U$ into $X$ .

I am just talking about a slight variant of what is done in the context of Sullivan models, and probably if I knew more about rational homotopy theory, I’d realize that what I am talking about is very well known under the name xyz, whatever.

In Sullivan models, one builds from any differential graded commutative algebra $CE (g, V)$ a simplicial manifold, by declaring the collection of $n$ -simplices to be the Hom-set ${Hom}_{dg - Algebras} (CE (g, V), Ω^{•} (Δ^{n})),$ where $Δ^{n} \subset ℝ^{n}$ is the standard $n$ -simplex in $ℝ^{n}$ and where $Ω^{•} (Δ^{n})$ is some version of differential forms on $Δ^{n}$ (usually some subalgebra of all differential forms on $Δ^{n}$ ).

Correct me if I am wrong, please, but this is my understanding.

So here I am talking about a slight variant of this idea: instead of looking at maps from $CE (g, V)$ to forms on the $n$ -simplex, I am looking at maps from $CE (g, V)$ to forms on any manifold and regard the collection of all these sets of maps not as a simplicial manifold, but as a generalized smooth space, in the standard sense of presheaf topoi.

I keep slowly expanding my notes on this. Maybe looking at these might make it clearer what I am trying to talk about.

This yields a contravariant functor

$S^{∞} \leftarrow DGCA : {Hom}_{dg - algebras} (- -, Ω^{•} (- -))$

CONTRAVARIANT WITH REPSEC TO THE FIRST –

AND THE SECOND??

My notation here was supposed to be suggestive, but maybe it obscures what’s going on: “ $S^{∞}$ ” means nothing but the category presheaves on my underlying site $S$ (of manifolds, say).

The functor ${Hom}_{dg - algebras} (- -, Ω^{•} (- -))$

is a contravariant functor, in its first argument, from DGCAs to such presheaves. So for any DGCA $CE (g, V)$ the thing ${Hom}_{dg - algebras} (CE (g, V), Ω^{•} (- -)) : S^{op} \to Set$ is a presheaf on $S$ (hence a contravariant functor on $S$ , yes).

So for any $CE (g, V)$ , this is just what we call $g$ -valued differential forms in section 2.5. This is simply what i mean here.

Posted by: Urs Schreiber on December 30, 2007 11:40 AM | Permalink | Reply to this

Read the post BF-Theory as a Higher Gauge Theory
Weblog: The n-Category Café
Excerpt: On interpreting BF-theory as a higher gauge theory.
Tracked: December 29, 2007 7:59 PM

Read the post Transgression of n-Transport and n-Connections
Weblog: The n-Category Café
Excerpt: On the general idea of transgression of n-connections and on the underlying machinery of generalized smooth spaces and their differential graded-commutative algebras of differential forms.
Tracked: December 30, 2007 6:40 PM

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

A somewhat more polished version is now available:

Part A, part B.

Posted by: Urs Schreiber on January 3, 2008 9:26 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

It’s very interesting ! I have a remark/question about bundle descent data.

In the ordinary case of a principal G-bundle, a descent object is given by a surjective submersion $p : Y \to X$ and a groupoid morphism $Y \times_{X} Y \to X$ . Now, the groupoid $Y \times_{X} Y$ has a canonical Morita morphism (induced by $p$ ) to the manifold $X$ viewed as a groupoid. Maybe I should recall that a Morita morphism is a “smooth” equivalence of groupoids. Therefore a descent data is a composition $X \leftarrow Y \times_{X} Y \to BG$ where the left arrow is a Morita morphism. Such composition are called generalized morphisms (at least by C*-algebras people). Note that Morita morphisms induce isomorphisms in cohomology, thus one can use both $H (X)$ and $H (Y \times_{X} Y)$ to define characteristic classes. This construction is a purely “smooth” analogue of the standard fact that principal G-bundles over a space X are equivalent to a homotopy class of maps from X to BG.

The idea can be generalized to n-groups-bundles as well. In fact, using this Lie groupoid point of view, Mathieu Stiénon and I have recently been working on similar ideas (for principal 2-bundles). It’s now available on arxiv: Groupoid extensions, principal 2-group bundles and characteristic classes . Our approach should be closely related to yours. I havn’t figured the details out yet but I feel that a g-bundle descent data (where g is the Lie algebra of a given 2-group) should be given by the de Rham complex of a 2-group bundle $Z$ Morita equivalent to the manifold X viewed as Lie 2-groupoid and a map from Z to the 2-group. The later map will induce a chain map from the de Rham complex of the 2-group to the de Rham complex of Z. There is probably some work to give a quasi-isomorphism in between CE(g) and the de Rham complex of the 2-group…

Posted by: Greg Ginot on January 9, 2008 9:58 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Greg,

many thanks indeed for you message!

I have not much time available right now, but let me quickly give some replies:

You wrote:

Therefore a descent data is a composition $X \leftarrow Y \times_{X} \to B G$ where the left arrow is a Morita morphism. Such composition are called generalized morphisms

Yes! Around here, we like to call these guys anafunctors. This is a perspective which has been greatly advertized by John Baez (see for instance his lecture notes “Quantization and cohomology”, week 23 and week 24), building on some observations his student Toby Bartels made. We once had a big discussion of this here in the thread Local Transition of Transport, Anafunctors and Descent of n-Functors. It plays a key role in much of what we are talking about here, in particular its generalization from mere bundles to bundles which connection, which I talk about at length in The first edge of the cube.

You further write: ” In fact, using this Lie groupoid point of view, Mathieu Stiénon and I have recently been working on similar ideas (for principal 2-bundles). It’s now available on the arxiv: Groupoid extensions, principal 2-bundles and characteristic classes.”

Oh, thanks, I hadn’t seen that! That’s interesting. (I am wondering: is Mathieu Stiénon the Mathieu who I met in Toronto last winter when he was a fellow at the Fields institute? After my talks on $n$ -bundles with connection I had a long discussion with some Mathieu, but I am afraid I cannot recall his last name, unfortunately… Sorry.)

I don’t have time to look at your article in detail right now, but maybe you can quickly answer the following question for me:

what happens in your theory when the 2-group in question is the strict version of the String-2group?

One of the motivations for our article was to prove that String 2-bundles have the same characteristic classes as the underlying $G$ -bundles, except that the first Pontrjagin class gets killed, as John discussed here.

Using our Lie $∞$ -algebra connection descent objects this becomes pretty obvious. Can you see that, too? That would be real cool. I need to read your paper. Will do so as soon as possible.

Posted by: Urs Schreiber on January 9, 2008 10:46 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Urs, thanks for the links !

You wrote:

I am wondering: is Mathieu Stiénon the Mathieu who I met in Toronto last winter

I don’t think so. However there was a very smart young french in Toronto last year called Mathieu Anel who is working on higher stacks and derived geometry. It might be him.

You wrote:

what happens in your theory when the 2-group in question is the strict version of the String-2group?

I read John’s post (following Jim’s advice) as well as one of yours and I got similar feeling. Roughly speaking, following the ideas in arXiv:0712.2069 , the string 2-group $String (G)$ gives rise to a fibration $[S^{1} \to 1] \to String (G) \overset{p}{\to} PG$ where $PG$ stands for the path group of $G$ (viewed as a 2-group) and $[S^{1} \to 1]$ is the 2-group associated to the crossed module $S^{1} \to 1$ . The cohomology of (the classifying space of) String(G) can then be computed using the Leray Spectral sequence (which is a spectral sequence of algebras). Since the classifying space of $[S^{1} \to 1]$ is a $K (ℤ,3)$ , the E_2-term of the spectral sequence is concentrated in bidegrees $(*,0)$ and $(*,3)$ , with $E_{2}^{p,0} = H^{p} (BG) = E_{2}^{p,3}$ . In other words, the $E_{2}$ -term is the (graded symmetric) algebra $H^{*} (BG) [x]$ where $x$ is of degree 3. The non-trivial differential is $d_{3} : H^{p} (BG) \to H^{p + 4} (BG)$ . It identifies with the derivation induced by $x \mapsto H \in H^{4} (BG)$ where $H$ is the canonical generator of $H^{4} (BG)$ corresponding to the canonical 3-form on $G$ (through the isomorphism $H^{n} (BG) ≅ H^{n - 1} (G)$ ). Therefore, $H (BString (G)) ≅ H^{*} (BG) / H$ .

Now, it is really easy to check that the characteristic classes constructed using the generalized morphisms/anafunctors picture in our paper arXiv:0801.1238 are the same as the classes of the underlying G-bundles, except for the first Pontrjagin class who get killed.

Indeed, given an anafunctor $X \leftarrow E \overset{f}{\to} String (G)$ , the characteristic classes considered in our paper arXiv:0801.1238 are obtained by taking the images of the classes in $H^{*} (BString (G))$ through the composition $H^{*} (BString (G)) \overset{f^{*}}{\to} H^{*} (E) ≅ H^{*} (X)$ . According to the above discussion, these classes coincides with the one induced by the composition $H^{*} (BG) \overset{p^{*}}{\to} H^{*} (BString (G)) \overset{f^{*}}{\to} H^{*} (E) ≅ H^{*} (X)$ .

Posted by: Greg Ginot on January 9, 2008 5:07 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Greg, that’s really nice.

Notice that in that entry which you looked at the cohomology of the String Lie 2-algebra was not really fully discussed. I later did a pedestrian proof that $H^{•} (CE (string (g))) ≃ H^{•} (g) / μ,$ for $μ$ the canonical 3-cocycle on the semisimple Lie algebra $g$ , and Danny Stevenson came up with a spectral sequence proof, probably essentially the one you just sketched.

Both of which we didn’t find nice enough for presentation, so in proposition 15 only the statement appears.

the characteristic classes constructed using the generalized morphisms/anafunctors picture in our paper arXiv:0801.1238 are the same as the classes of the underlying G-bundles, except for the first Pontrjagin class who get killed.

Very well. Cool.

We find that this is actually just a special case of the whole infinite series of such situations:

for every Lie $∞$ -algebra $g$ and every degree $(n + 1)$ -cocycle $μ \in H^{•} (CE (g))$ , there is a Lie $∞$ -algebra $g_{μ}$ which sits in a $b^{n - 1} u (1)$ -extension of $g$ in that we have an exact sequence $b^{n - 1} u (1) \to g_{μ} \to g$ and that $g_{μ}$ $n$ -bundles have the same characteristic classes as the underlying $g$ -bundles, except that the class corresponding to the invariant polynomial which $μ$ transgresses to gets killed.

Can you similarly generalize your results to higher Lie $n$ -groups? Probably using smooth Kan-complexes following Getzler and Henriques?

Posted by: Urs Schreiber on January 10, 2008 11:08 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

You wrote :

Can you similarly generalize your results to higher Lie n-groups? Probably using smooth Kan-complexes following Getzler and Henriques?

I guess so, but it might require some work.
I’m not sure if you can avoid dealing with smooth Kan complexes in general. However, for this kind of examples, it might be enough to use smooth n-categorical groups (i.e. the smooth analogue of Loday’s definition in spaces with finitely many nontrivial homotopy groups ). I’ll have to think about it !

Posted by: Greg Ginot on January 11, 2008 9:22 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

I would think ordinary dg homological algebra/rational homotopy theory woudl suffice
without using smooth Kan-complexes following Getzler and Henriques?

Posted by: jim stasheff on January 13, 2008 7:59 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

I would think ordinary dg homological algebra/rational homotopy theory woudl suffice without using smooth Kan-complexes following Getzler and Henriques?

I just meant that when doing the “ingrated theory” where an $n$ -bundle descent datum is a morphism of $n$ -groupoids, you need to get hold of these $n$ -groupoids. For low $n$ it is convenient to use concrete bottom-up realizations. For general $n$ the tool of choice the the top-down approach of Kan complexes.

(Though I started thinking about whether maybe qDGCAs might want to rather integrate to presheaves on $ω Cat$ or the like. But I’ll have to keep thinking before I can provide anything of interest here…)

Posted by: Urs Schreiber on January 14, 2008 6:04 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

$MathML-enabled post (click for more details).$

Greg Ginot wrote:

The cohomology of (the classifying space of) $String (G)$ can then be computed using the Leray Spectral sequence (which is a spectral sequence of algebras).

Matt Ando pointed out this argument when I asked about the cohomology of $B (String (G))$ at the 2007 Abel Symposium. That’s how I knew the cohomology of $B (String (G))$ by the time I gave a talk on higher gauge theory and the string group later that summer — see the last page.

I guess anyone who’s good at spectral sequences can do this calculation. I’m not! But Danny Stevenson is. We’re coming out with a paper on this sort of stuff pretty soon. It will contain a version of this argument, and I just want to make it clear that we didn’t steal this argument from you. Matt Ando gave it to us.

Posted by: John Baez on January 11, 2008 10:10 PM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Which spectral sequence(s) are we talking about? any of the three or more relating
String(G) and BString(G)??

or for any of those relating String(G) to G??

Posted by: jim stasheff on January 12, 2008 1:16 AM | Permalink | Reply to this

Re: Lie oo-Connections and their Application to String- and Chern-Simons n-Transport

Jim wrote:

Which spectral sequence(s) are we talking about?

Basically the one that Greg described. My paper with Danny should hit the arXiv in a couple of days, and that’ll fill in some details.

Posted by: John Baez on January 13, 2008 7:06 AM | Permalink | Reply to this

Gysin sufficient, no need for spec seq

The string 2-group String(G) gives rise to a fibration [S 1→1]→String(G)→pPG where PG stands for the path group of G (viewed as a 2-group) and [S 1→1] is the 2-group associated to the crossed module S 1→1. The cohomology of (the classifying space of) String(G) can then be computed using the Leray Spectral sequence (which is a spectral sequence of algebras). Since the classifying space of [S 1→1] is a K(ℤ,3), the E_2-term of the spectral sequence is concentrated in bidegrees (*,0) and (*,3), with E 2 p,0=H p(BG)=E 2 p,3. In other words, the E 2-term is the (graded symmetric) algebra H *(BG)[x] where x is of degree 3. The non-trivial differential is d 3:H p(BG)→H p+4(BG). It identifies with the derivation induced by x↦H∈H 4(BG) where H is the canonical generator of H 4(BG) corresponding to the canonical 3-form on G (through the isomorphism H n(BG)≅H n−1(G)).
Therefore, H(BString(G))≅H *(BG)/H.

IFF I understand this correctly, the FIBRE is K(Z,3) and the base is BG
hence with characteristic 0 coefficients, this looks like a fibration with S^3 as fibre, hence we have a Gysin sequence with no need to appeal to spectral sequences

the usual bigrading is (base,fibre) not (fibre,base)
then the differential would be down and to the right
as expected

Posted by: jim stasheff on January 13, 2008 2:35 PM | Permalink | Reply to this

Re: Gysin sufficient, no need for spec seq

$MathML-enabled post (click for more details).$

Oh yes Jim, you’re right ! It’s a very nice comment

The n-Category Café

Skip to the Main Content

December 25, 2007