On Weak Cokernels for 2-Groups

October 17, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

In Detecting higher order necklaces I mentioned how

P. Carrasco A. R. Garzó́n and E. M. Vitale
On categorical crossed modules
Theory and Applications of Categories, Vol. 16, 2006, No. 22, pp 585-618

is related to

David Roberts, U.S.
The inner automorphism 3-group of a strict 2-group
arXiv:0708.1741
(html).

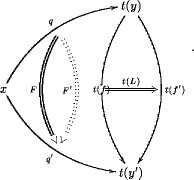
with the relation becoming obvious after drawing some diagram. This discussion, quite brief, but the picture provided there is useful to keep in mind, I have now prepared here:

On weak cokernels

This blog entry is hence mainly a private message to David Roberts (since it builds on our discussion of inner automorphism $(n+1)$ -groups). And maybe to Todd Trimble (since it builds on our discussion of tangent categories (pdf, html). And to Jim Stasheff (since it is going to be applied to obstructions to lifts of $n$ -Cartan connections (slides, BIG diagram)). And to John Baez of course, from whome I am hoping to receive more hints on how to think of the big picture . And to Bruce Bartlett, with whom I was talking about this here and by email.

Hence a blog post.

You’ll see that this issue of weak cokernels of 2-groups is the integral version of what I had started to discuss at the level of Lie $n$ -algebras in

Obstructions and cokernels of Lie n-algebra morphisms
(pdf)
(html).

$MathML-enabled post (click for more details).$

To whetten your appetite, a degenerate (low $n$ ) version of what I am trying to get at here is related to Schreier theory:

Given a sequence

$K \to G \to B$

of groups, we cannot, in general, find a splitting $G \leftarrow B$ which is a group homomorphism. But the failure is “coherent”.

One way to say this is:

denote by

$(K \to G)$

the weak cokernel of the map $K \to G$ . This is nothing but the 2-group defined by the crossed module of the same name $K \to G$ !

And this 2-group is equivalent to $B$

$(K \to G) \simeq B$

This means we always have morphisms

$B \hookrightarrow (K \to G)$

which are equivalences.

These are best thought of as pseudofunctors on the corresponding one-object 2-groupoids:

on morphisms these functors are nothing but lifts

$G \leftarrow B$

that may fail to respect composition, strictly. But the failure – the compositor – is something in $K$ , indeed a 2-morphism in $\Sigma(K \to G)$ .

Now, the 2-group $(K \to G)$ sits inside the 2-group $\mathrm{AUT}(K)$ ,

$(K\to G ) \to \mathrm{AUT}(K)$

of automorphic functors on $\Sigma K$

Notice how this is a nice way to understand lifting gerbes:

A $B$ -bundle is given by a cocycle which can be thought of as lots of triangles labeled in $B$ .

We may ask if we can lift these labels to labels in $G$ . In general we cannot. But what we can always do is lift them to labels in $(K \to G)$ : because that simply means that we choose any lifts, and then label the interior of the triangle with the mistake in K that we made thereby.

So every $B$ -cocycle is a $(K \toG)$ - cocycle.

We may want to characterize the “mistakes in $K$ ” that we made by this attempted lift. To find these, we check which part of our failed lift doesn’t sit entirely in B, so we look at the cokernel of the canonical inclusion

$G \hookrightarrow (K \to G)$

(notice that we are using here that the “puffed up” version $(K \to G)$ of $B$ has the property that what used to be a surjection $G \to B$ now becomes an inclusion!)

which is simply $\Sigma K$

$G \to (K\to G ) \to \Sigma K$

Postcomposing our labelling of triangles with this morphism

$(K \to G) \to \Sigma K$

simply forgets the labels of the boundaries of the triangle and only remembers the $K$ -labels in their interior. This is now the 2-cocycle describing a $\Sigma K$ - 2-bundle. And this is the lifting 2-bundle (lifting gerbe).

If this 2-cocycle is nontrivial it means that the failures to lift that we made are real and cannot be undone by a more clever lift. If that 2-cocycle however is a 2-coboundary it means that there is a more clever choice of lift which produces no failure: the lifting gerbe trivializes.

You have maybe seen the pictures illustrating this on slides 322 onwards in my slides.

Posted at October 17, 2007 10:34 PM UTC

TrackBack URL for this Entry: https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1467

20 Comments & 5 Trackbacks

Re: On Weak Cokernels for 2-Groups

I’m on it.

Processing…

Posted by: David Roberts on October 18, 2007 6:05 AM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

I’m on it.

Processing…

Okay, great. Let me point out more clearly which points need clarification:

while the discussion of the mapping cone $(K \to G)$ itself can be done entirely in the world of strict 2-groups, the morphism

$B \to (K \to G)$

is not only pseudo (a weak 3-functor) but needs to be something like “ana-pseudo” for Lie 2-groups: even the failed lifts don’t exist globally.

I am confident that this has to all work out, since it did in the Lie $n$ -algebra version of the same discussion (beware, though, this is the old version of my file which needs some rectification somewhere, will try to update it) but it certainly requires further discussion.

I need to further study CarrascoGarzónVitale to understand to which degree this is addressed by them.

Posted by: Urs Schreiber on October 18, 2007 11:55 AM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

What you explain in your note seems to be an application of the following fact : the weak cokernel of a morphism of 2-groups seen as a morphism of discrete 3-groups is the same as the weak kernel of the suspension of this morphism.

Let me explain this one dimension lower. If you start with a morphism of groups $t:G\to H$ , you can on the one hand take the weak cokernel of $t$ seen as a morphism of discrete 2-groups, you get a pointed groupoid $\Coker t$ , which is a 2-group if you start with a crossed module (this is the “realization” of the crossed module as a 2-group).

On the other hand, you can take the weak kernel of the suspension of $t$ . In general, the (weak) kernel of a morphism of pointed groupoids $T:\mathbf{G}\to\mathbf{H}$ is the pointed groupoid $\mathrm{Ker T}$ such that

• the objects are given by an object $A$ of $\mathbf{G}$ and an arrow $\phi:FA\to *$ in $\mathbf{H}$ (where $*$ is the point of $\mathbf{H}$ );

• the arrows $(A,\phi)\to(A',\phi')$ are arrows $a:A\to A'$ in $\mathbf{H}$ such that $\phi' Fa = \phi$ .

In the case of $\Sigma t:\Sigma G\to\Sigma H$ , you get what you call $T^t \Sigma G$ , and so you get back the cokernel of $t$ seen as a morphism of discrete 2-groups.

There is then a sequence of pointed groupoids $G\overset{t}\to H\to \mathrm{Coker} t\simeq\mathrm{Ker} \Sigma t\to\Sigma G\overset{\Sigma t}\to\Sigma H.$

If you start with a morphism of 2-groups, you’ll get the same situation, with pointed 2-groupoids.

Posted by: Mathieu Dupont on October 18, 2007 12:47 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Thanks for this comment. You seem to be well familiar with this. Can you suggest more literature? Is this standard?

There is then a sequence of pointed groupoids

$G \stackrel{t}{\to} H \to \mathrm{Coker}(t) \simeq \mathrm{Ker}( \Sigma t) \to \Sigma G \stackrel{\Sigma t}{\to} \Sigma H$

Ah, that’s great. I hadn’t thought about it quite this way yet.

But it seems to point in a direction that I was wondering about a bit:

shouldn’t that situation be closely related to the way every short exact sequence of topological groups

$0 \to A \to B \to C \to 0$

gives rise to a long exact sequence in homotopy

$\cdots \to \pi_n(A) \to \pi_n(B) \to \pi_n(C) \stackrel{\delta}{\to} \pi_{n-1}(A) \to \cdots$ ?

It’s not entirely clear to me yet, but my gut feeling is that if we replace homotopy groups here with the corresponding fundamental $n$ -groups of a space, then the long sequence in homotopy should be a special case of what we’d obtain from the picture you just sketched in the case that further suspensions are possible

$\cdots \to G \stackrel{t}{\to} H \to \mathrm{Coker}(t) \simeq \mathrm{Ker}( \Sigma t) \to \Sigma G \stackrel{\Sigma t}{\to} \Sigma H \to \mathrm{Coker}(\Sigma t) \simeq \mathrm{Ker} (\Sigma^2 t) \to \Sigma^2 G \stackrel{\Sigma^2 t}{\to} \Sigma^2 H \to \cdots \,.$

Could that be right?

Posted by: Urs Schreiber on October 18, 2007 1:39 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Thanks for this comment. You seem to be well familiar with this. Can you suggest more literature? Is this standard?

I’m finishing my PhD thesis with Enrico Vitale.

There is a connection with the long exact sequence in homotopy : they are both a special case of the following fibration sequence of pointed groupoids (see Gabriel and Zisman, “Calculus of fractions and homotopy theory”, chapter V). For a pointed groupoid $X$ , let $\Omega X$ be the weak kernel of the unique pointed functor $0\to X$ (where $0$ is the one object, one arrow pointed groupoid), i.e. $\Omega X$ is the group $X(*,*)$ (where $*$ is the point of $X$ ) seen as a discrete pointed groupoid. Then for every pointed functor $F:X\to Y$ , there is a sequence $0\simeq \Omega(\Omega Y)\to\Omega\Ker F\to\Omega X\overset{\Omega F}\to\Omega Y\to\Ker F\to X\overset{F}\to Y,$ where each arrow is equivalent to the weak kernel of the following one.

If you apply $\pi_0$ to this sequence, you get a “long homotopy sequence” of pointed sets and groups, since $\pi_0\Omega=\pi_1$ : $0\to\pi_1(\Ker F)\to\pi_1(X)\overset{\pi_1(F)}\to\pi_1(Y)\to\pi_0(\Ker F)\to\pi_0(X)\overset{\pi_0(F)}\to\pi_0(Y)$

Now, if you have a group homomorphism $f:X\to Y$ , you can apply the first sequence above to $\Sigma f$ , and since $\Omega\Sigma X$ is $X$ seen as a discrete groupoid, you get the following sequence of pointed groupoids. $0\to\Ker f\to X\overset{f}\to Y\to\Ker\Sigma f\to\Sigma X\overset{\Sigma f}\to\Sigma Y$

So these are not the same sequences, one is a sequence of pointed sets constructed from a morphism of pointed groupoids, and the other a sequence of pointed groupoids constructed from a morphism of groups.

You can extend these sequences with the weak cokernel. Corollary 2.7 in Bourn and Vitale, Extensions of symmetric cat-groups* gives for a morphism of symmetric 2-groups $F:X\to Y$ the following sequence of abelian groups : $0\to\pi_1(\mathrm{Ker} F)\to\pi_1(X)\overset{\pi_1 F}\to\pi_1(Y)\to\pi_1(\mathrm{Coker} F)\simeq\pi_0(\mathrm{Ker} F)\to\pi_0(\X)\overset{\pi_0(F)}\to\pi_0(Y)\to\pi_0(\mathrm{Coker} F)\to 0$

For higher dimensions, Beppe Metere has studied the “ziggurat of exact sequences of n-groupoids”, but there is still no available reference as far as I know.

*On the same page, there is also “A higher dimensional homotopy sequence”, by Grandis and Vitale.

Posted by: Mathieu Dupont on October 22, 2007 12:33 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Mathieu,

this is most interesting. I am grateful that you took the time to share this information. This looks like it is the answer to something I have been struggling with for a while now.

I’m printing the references you provided, will have a look at them on the plane tomorrow (unless I fall asleep, as usual ;-).

For higher dimensions, Beppe Metere has studied the “ziggurat of exact sequences of $n$ -groupoids”, but there is still no available reference as far as I know.

Googling, I found at least

Beppe Metere, (The Ziggurath of) exact sequences of $n$ -groupoids (handwritten notes)

which already looks very helpful.

Thanks again! I might get back to you with further questions/comments here once I have had a chance to look into this.

Posted by: Urs Schreiber on October 23, 2007 10:26 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

The following may or may not be implicit in what Mathieu Dupoint said above, or in the literature which he provided, I haven’t fully absorbed that yet.

But today I realized that the construction of weak cokernels that I am talking about, is apparently nicely related to relative homotopy groups, in a very vivid way.

So recall the construction I am talking about:

given two 2-groupoids $C$ and $D$ , and a 2-functor $t : C \to D$ which is “sufficiently injective” (let’s assume for simplicity that its component map is an injective maps on objects, morphisms and $2$ -morphisms), then the weak cokernel of $t$ is the 2-groupoid

a) whose objects are 2-functors from the “fat point” $(\bullet \stackrel{\simeq}{\to} \circ)$ into $D$

b) whose morphisms are transformations of such 2-morphisms restricted to be trivial on $\bullet$ and to lie in the image of $t$ on $\circ$

c) 2-morphisms are modifications of such transformations, whose components lie in the image of $t$ .

So a 2-morphism in $\mathrm{wcoker}(t)$ looks like a diagram of the form

in $D$ , with $L$ in $C$ .

Notice that this looks a bit like a 2-disk in $D$ whose boundary (2-1)-sphere is in the image of $t$ .

But this is the way relative homotopy groups are defined.

Let $X$ be a topological space and $t : A \hookrightarrow X$ a subspace, then the elements of the $n$ -homotopy group of $X$ relative to $A$ are those maps into $X$ which look like maps of the $n$ -sphere into $X$ once we think of $A$ as being a single point.

More precisely, $\pi_n(X,A) = \left\lbrace f : D^n \to X | \partial D^n \subset t(A) \right\rbrace$ (I am suppressing the basepoints and the respect for them).

Clearly, this formula expresses the same kind of condition that enters the construction of the diagram displaeyed above.

In fact, I think that if I assume my 2-groupoids $C$ and $D$ to be the fundamental 2-groupoids $\Pi_2$ of $A$ and $X$ , respectively, then then the weak cokernel of $\Pi_2(A) \stackrel{\Pi_2(t)}{\to} \Pi_2(X)$ is pretty much the 2-groupoid version of the $t$ -relative homotopy 2-group.

If you see what I mean.

And indeed, the relative homotopy groups fit into a long exact sequence $\pi_n(A) \stackrel{t}{\to} \pi_n(X) \to \pi_n(X,A) \to \pi_{n-1}(A) \to \cdots$

which seem to correspond to precisely the corresponding long sequences of $n$ -groupoids that we were talking about above.

(Sorry for the vagueness of these statements, I am just trying to quickly communicate a rough observation here.)

Posted by: Urs Schreiber on November 1, 2007 6:26 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

I am suppressing the basepoints and the respect for them.

Gosh Urs - are you disrespecting basepoints? The homotopy police are not going to take kindly to this…!

Posted by: Bruce Bartlett on November 2, 2007 10:39 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

Gosh Urs - are you disrespecting basepoints?

No, suppressing them, notationally that is.

Posted by: Urs Schreiber on November 4, 2007 4:18 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

Thanks for constructing at least half the bridge between cats and homtopy theory.

0≃Ω(ΩY)→ΩKerF→ΩX→ΩFΩY→KerF→X→FY,
where each arrow is equivalent to the weak kernel of the following one.

In homotopy theory, as I’m sure you know but let’s let the rest of the blog in on the story:

for any map of spaces f: X –> Y
we have the homtopy fibre H_f (apparently to be called weak kernel) and a long sequence

…–> Omega H_f –> Omega X —> Omega Y –> H_f –> X –> Y

where each space is homotopy equvalent to the corresponding homotopy fibre

on the other hand, we have the mapping cone C_f and the Barratt-Puppe sequence

X –> Y –> C_f –> Sigma X –> Sigma Y –>…

N.B. Here Sigma means topological suspension NOT BX

also any map can be decomposed via a
fibration…

Posted by: jim stasheff on November 3, 2007 12:26 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

Having seen no response to this, I’ll auto-respond!

In so far as hihger cats mimic (part of?) homotopy theory, I think it’s really important that we agree or establish an alternative:
weak kernel = homotopy fibre?
weak cokernel = homotopy quotient?
mapping cone = cofibre = ??

and we should really do something about the conflict about Sigma

e.g. for ordinary top groups
Sigma G is the suspension = projective line whihc is a subspace of BG = `infinite proj space’

speak now or foreever…

Posted by: jim stasheff on November 6, 2007 5:13 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

and we should really do something about the conflict about Sigma

Perhaps one can write something like $A^{[n]}$ for something where the $n$ -cells are given by the Abelian group $A$ ? You can then also write things like $G^{[1,2]}$ to mean a group $G$ , thought of as a one-object 2-category with the elements of $G$ being the one-cells, and only identity 2-cells.

Posted by: Bruce Bartlett on November 7, 2007 12:03 AM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Sorry for not replying sooner. It’s not due to lack of interest, but rather the opposite: I feel I need to think about the answer but am distracted due to travelling.

My personal feeling is this:

all the identifications you indicated are certainly morally right, and probably can be made into precise statements about certain things being equivalent.

But at the same time, my personal impression is that we are not quite at that point yet where we don’t run into trouble by using all these terms, topological ones on one side and category theoretic ones on the other, as if we had already fully established that and how they are precisels “the same”.

For instance: while maybe the choice of “ $\Sigma$ ” for the operation of

$\Sigma$ : turning a $k$ -tuply monoidal $n$ -catgegory into a $(k-1)$ -tuply monoidal $(n+1)$ -category

is not optimal (I seem to remember that I adopted this notation from Aaron Lauda), I do think that it is not unimportant not to write $B$ for $\Sigma$ .

It is true that under the classifying space functor $|\cdot|$ , $\Sigma G$ turns into $|\Sigma G| = B G \,,$ but my feeling is that until we have reached the point – maybe in one or trwo decades (?!) – that we all feel safe with completely identifying the world of $n$ -categories with the world of spaces, we will run into the risk of confusing ourselves and our audiences by treating these terms all as established synonyms.

While from some big bird’s eye point of view a category (or a groupoid, anyway) is a space, for my practical purposes I certainly want to distinguish between, for instance, the finite category $\Sigma G$ , which is really just a finite set with a composition operation on it, and the “huge” space $B G$ obtainable from it.

I am well aware that at various places in the literature the symbol $B G$ is used for things less “spacelike” than the classifying space of $G$ , but I am feel hesitant to add to that by writing $B G$ for $\Sigma G$ .

Similar comments I would make concerning your other remarks.

While it is certainly true that weak cokernels play the role of homotopy fibers, etc., I wouldn’t want – not until some point in the future when we all agree by default on that and how spaces are the same as $n$ -categories generally – to forget that while morally the same, they differ at least in terms of which they are defined.

Maybe it’s just me being slow and hesitant and overcautious. But in any case, that’s my comment to your remark.

Posted by: Urs Schreiber on November 7, 2007 7:34 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

I see your point but still would like something onther that Sigma for you cat construction. Even S or s for shift.
as for something versus it’s realization
some people get by with a change in font
BG for the realization of say {\mathcal B} G

If weak kernel is not always satisfying the analogous universal property in cats to homotopy fibre in spaces,
then let’s establish when and where they do agree

Posted by: jim stasheff on November 8, 2007 3:04 AM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

As a homotopy theorist, I see
G→tH→Coker(t)≃Ker(Σt)→ΣG→ΣtΣH

as corresponding but roughly to what I’m familiar with:

G –> H –> H_G meaning the homotopy quotient which is of the homtopy type of H/G
when G acts nicely

up to homotopy, the sequence continues

G –> H –> H_G –> BG –> BH

in which any three terms in a row can be regarded as fibre –> total space –> base

IF G is a normal subgroup of H
we can go one step further

G –> H –> H_G –> BG –> BH –> B(H_G)

If G is abelian so BBG exists, yet one more step

If G and H are abelian, we can go on forever

on the other side, we can take based oop spaces and back up forever

–> \Omega G –>\Omega h –> \Omega(H_G)–> G –> H –> H_G –> BG –> BH

Posted by: jim stasheff on December 15, 2007 10:07 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Given a short exact sequence of groups

$0 \to K \stackrel{t}{\to} G \to B \to 0$

what do you know about the (weakly) universal morphism $f$

$\array{ K &\stackrel{t}{\to}& G &\to& \mathrm{coker}(t) \\ && \downarrow & \swarrow_{f} \\ && B }$

in the case of Lie groups, with

$\mathrm{coker}(t) = (K \stackrel{t}{\to} G)$

the weak cokernel?

The morphism $f : (K \stackrel{t}{\to} G) \to B$

should be an equivalence in a suitable sense, but its weak inverse may not be smooth.

I’d think we’d need ana-2-functors to handle this, or something similar. But maybe you know more about this.

Posted by: Urs Schreiber on October 18, 2007 2:17 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

Thanks for taking the time to explain this, Urs – I’ll try to read this more carefully today.

Allow me to make one obnoxious comment about an idiomatic English expression: it should be “whet your appetite”, meaning “stimulate your appetite”. “Whet” literally means “sharpen”: a whetstone is something used to sharpen knives or tools.

Feel free to reciprocate if you see me butchering your native language, e.g., by omitting the umlaut from “doppelgänger”, as I did recently. (My wife is of German ancestry and speaks fluently, but I never picked it up.)

Posted by: Todd Trimble on October 18, 2007 1:30 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

one obnoxious comment about an idiomatic English expression

Thanks a lot! I appreciate it. It’s fixed now.

I am actually afraid that you all are being way too polite with me in not correcting me more often.

This entire blog here serves one big purpose for me: find my mistakes. :-) Mostly mathwise, but if I eventually improve my English this way, it wouldn’t hurt either.

Posted by: Urs Schreiber on October 18, 2007 1:44 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

Improved version of

On weak cokernels

now avaialble, incorporating a couple of improvements made by David Roberts:

The pullback property of $T^t \Sigma G_{(2)}$ has been put in a nicer way, the condition on the morphism $H_{(2)} \to G_{(2)}$ stated better (needs to be faithful on the underlying 1-groupoids). And my funny comment in the introduction has been clarified a little more.

Posted by: Urs Schreiber on October 18, 2007 4:40 PM | Permalink | Reply to this

Re: On Weak Cokernels for 2-Groups

$MathML-enabled post (click for more details).$

I have now polished my former discussion of weak cokernels of Lie $n$ -algebras and merged it with the discussion of weak cokernels of Lie 2-groups by means of mapping cones/tangent categories. The result is here:

On weak cokernels

Then I have incorporated this discussion more fully in my Wiki-substitute called

String- and Chern-Simons $n$ -Transport

See

- section $n$ -Categorical background, subsection Mapping cones

as well as

- section String- and Chern-Simons $n$ -transport, subsection Obstruction theory

Posted by: Urs Schreiber on October 19, 2007 4:33 PM | Permalink | Reply to this

Read the post On Lie N-tegration and Rational Homotopy Theory
Weblog: The n-Category Café
Excerpt: On the general ideal of integrating Lie n-algebras in the context of rational homotopy theory, and about Sullivan's old article on this issue in particular.
Tracked: October 20, 2007 4:33 PM

Read the post BV for Dummies (Part V)
Weblog: The n-Category Café
Excerpt: Some elements of BV formalism, or rather of the Koszul-Tate-Chevalley-Eilenberg resolution, in a simple setup with ideosyncratic remarks on higher vector spaces.
Tracked: October 30, 2007 10:09 PM

Read the post n-Bundle Obstructions for Bruce
Weblog: The n-Category Café
Excerpt: On the global description of n-bundles obstructing lifts through shifted central extensions.
Tracked: November 4, 2007 5:55 PM

Read the post Lie oo-Connections and their Application to String- and Chern-Simons n-Transport
Weblog: The n-Category Café
Excerpt: A discussion of connections for general L-infinity algebras and their application to String- and Chern-Simons n-transport.
Tracked: January 9, 2008 10:20 AM

Read the post Construction of Cocycles for Chern-Simons 3-Bundles
Weblog: The n-Category Café
Excerpt: On how to interpret the geometric construction by Brylinksi and McLaughlin of Cech cocycles classified by Pontrjagin classes as obstructions to lifts of G-bundles to String(G)-2-bundles.
Tracked: February 12, 2008 1:42 PM

The n-Category Café

Skip to the Main Content

October 17, 2007