Zoo of Lie n-Algebras

May 10, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

We would like to share the following:

Jim Stasheff & U. S.
Zoo of Lie $n$ -Algebras
(pdf)

Abstract:

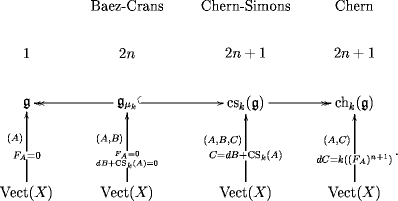
Higher order generalizations of Lie algebras have equivalently been conceived as Lie $n$ -algebras, as $L_{∞}$ -algebras, or, dually, as quasi-free differential graded commutative algebras (quasi-“FDA”s, of “qfDGCA”s).

Here we present a menagerie of examples concentrated in low degrees, study their morphisms and discuss applications to higher order connections, in particular String 2-connections and Chern-Simons 3-connections.

I’d be grateful for comments.

$MathML-enabled post (click for more details).$

This is work that has grown out of developments that I talked about in these entries:

From Loop Groups to 2-Groups

PSM and Algebroids, III

PSM and Algebroids, V

$n$ -Curvature

Chern-Simons Lie-3-Algebra Inside Derivations of String Lie-2-Algebra

10D SuGra 2-Connection

SuGra 3-Connection Reloaded

Posted at May 10, 2007 5:54 PM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1272

30 Comments & 10 Trackbacks

Re: Zoo of Lie n-Algebras

Very cool paper, though often above my level. But what is needed to move from an unstructured “zoo” or “menagerie” to a more complete classification? Is there something like a lattice of such examples? Is there a “height” metric according to which one knows that one has the “smallest” example? What finite objects get their interesting properties from entities in the zoo?

Posted by: Jonathan Vos Post on May 10, 2007 7:55 PM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

But what is needed to move from an unstructured “zoo” or “menagerie” to a more complete classification?

Right, very good question.

Before commenting on that, let me first put this good question in the historical perspective by quoting the very first sentence of

M. Daily, T. Lada, A finite dimensional $L_{∞}$ -algebra example in gauge theory (ps)

(from 2005) where it says:

Although $L_{∞}$ algebras (or sh Lie algebras) have been objects of much research during the past several years, concrete examples of these structures remain somewhat elusive.

Given that state of the art, the next best thing one should hope to obtain is certainly a good inventory of examples.

And more: we don’t just want arbitrary examples, we want some that actually occur in nature – and we want to gain something for our other tasks by identifying Lie $n$ -algebras where they have previously remained unidentified (or addressed, irritatingly, as “soft group manifolds”).

Daily and Lada in the above paper end their introduction with the sentence

We leave it as a challenge to the physicists to develop a physical model whose gauge transformations are described by this algebraic examples.

So that’s a solution looking for a problem. We’d rather have it the other way round.

I hope this makes it look more pardonable that the title of our document contains the word “zoo” without it being preceeded by the words “taming of the” (as in the famous Moore-Seiberg paper).

That said, I would like to emphasize that the bulk of the paper goes into considerably more structural investigations than title might suggest.

While lots and lots clearly remains to be better understood, we do amplify a couple of striking patterns that do seem to have significance. Among them clearly is the $inn$ -construction, as discussed in the section “Main Results”.

On the other hand, as mentioned in the section “open problems” there are indications that there is a major structural issue here which we appear to be scratching the surface of – but not more.

Well I am being a little vague here, and that alone is of course part of the answer to your problem: much more needs to be understood, certainly.

But to close with something non-vague, I should at least recall that for semistrict Lie 2-algebras, John Baez and Alissa Crans proved a classification result saying that these are classified by

- a Lie algebra $L$

- an $L$ -module $M$

- an element in $H^{3} (L, M)$ .

This parallels a similar result for Lie 2-groups, given by John Baez and Aaron Lauda.

Posted by: urs on May 10, 2007 9:04 PM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Congratulations for assembling this menagerie, Urs and Jim!

I should at least recall that for semistrict Lie 2-algebras, John Baez and Alissa Crans proved a classification result saying that these are classified by

- a Lie algebra $L$

- an $L$ -module $M$

- an element in the Lie algebra cohomology group $H^{3} (L, M)$ .

In fact we go a bit further: we classify semistrict Lie $n$ -algebras $C$ that are only nontrivial on the bottom and the top — that is, with only the chain groups $C_{0}$ and $C_{n - 1}$ nonvanishing. These are classified by:

- A Lie algebra $L$

- An $L$ -module $M$

- an element in the Lie algebra cohomology group $H^{n + 1} (L, M)$

This reduces to the classification you mentioned when $n = 2$ . But, in one small way it’s simpler when $n$ > $2$ : in this case we just have $L = C_{0}$ and $M = C_{n - 1}$ .

Of course, one would really like to classify all semistrict Lie $n$ -algebras. This should also be possible using cohomology — but not the cohomology of Lie algebras. Rather, we should use the cohomology of Lie $(n - 1)$ -algebras!

The idea is that given a Lie $n$ -algebra $L_{n}$ , we can form a Lie $(n - 1)$ -algebra $L_{n - 1}$ by ‘killing off the $n$ -chains’. It should be possible to completely describe $L_{n}$ in terms of $L_{n - 1}$ , a module $M_{n}$ of $L_{n - 1}$ , and a cohomology class in $H^{n + 1} (L_{n - 1}, M_{n})$ .

This recursive analysis of a Lie $n$ -algebra in terms of ‘layers’ will be familiar to people who know about Postnikov towers. People who don’t can find an explanation in my Lectures on $n$ -categories and cohomology. See especially the section on ‘cohomology: the layer-cake philosophy’.

Posted by: John Baez on May 11, 2007 3:31 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

I wrote:

While lots and lots clearly remains to be better understood, we do amplify a couple of striking patterns that do seem to have significance. Among them clearly is the $inn$ -construction

I have now included a definition of the general operation $inn (\cdot) : (Lie - n - algebras) \to (Lie - (n + 1) - algebras)$ in section 3.3.

By itself it’s not really deep, but it clarifies a lot of things, I think.

A nonflat $n$ -connection with values in the Lie $n$ -algebra $𝔤_{(n)}$ is a morphism $d curv : Vect (X) \to inn (𝔤_{(n)}) .$ The general construction applies in particular to the 11-dimensional supergravity 3-form, and hence a field configuration of 11-dimensional supergravity should be a morphism $d curv : Vect (X) \to inn (sugra (10,1)) .$

This is now discussed in a little more detail at the end (but still not sufficiently).

It seems to me that this inn-construciton here automatically enforces what are known as the “rheonomy constraints” in the D’Auria-Fré-like formulation of supergravity, which says that after introducing what they call “Cartan integrable systems” one wants the curvature of the SuGra 3-form to really be a 4-form on spacetime, not something funny.

But that’s precisely what the inn-construction gives you.

Posted by: urs on May 11, 2007 6:15 PM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

What […] objects get their interesting properties from entities in the zoo?

Quantum field theories.

One major point is that we present a Lie 3-algebra (7.1.3) which should be the structure Lie 3-algebra governing Chern-Simons theory.

And it is “trivialized” by a string-connection. The inclusion $\begin{matrix} {string}_{k} (𝔤) & ↪ & inn ({string}_{k} (𝔤)) \\ ↑^{\sim} & ↑ \\ 𝔤_{k} & ↪ & {cs}_{k} (𝔤) \end{matrix}$ is, as we show, the Lie $n$ -algebra version of the statement that a string connection trivializes Chern-Simons theory (section 5.2 in What is an elliptic object?).

(This is, though, I should add, not really explained explicitly in the text, at the moment.)

And that is closely related to 10-dimensional supergravity , the heterotic string and the Green-Schwarz mechanism (see (7.2.6)).

And then there is the Lie 3-algebra which makes 11-dimensional supergravity manifestly a higher gauge theory (7.1.4, but this discussion is, as you can see, not finished yet).

And then, as mentioned in the section “open problems”, there should be a Lie $n$ -algebra somehow unifying these last three items.

In a word: like to every Lie algebra you can associate a (number of) gauge theory(ies), for every Lie $n$ -algebra you get corresponding higher gauge theories.

Posted by: urs on May 10, 2007 9:20 PM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Urs wrote:

What […] objects get their interesting properties from entities in the zoo?

Quantum field theories.

And more generally: anything that has continuous symmetries, symmetries between symmetries, symmmetries between symmetries between symmetries… and so on to the $n$ th level, will have a Lie $n$ -algebra associated to it!

Posted by: John Baez on May 11, 2007 5:55 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Just above proposition 5 you mention $INN (G)$ and I just realised that it is the groupoid version of $EG$ , namely the realisation of it is Milnor’s universal bundle. This begs the question: what is the corresponding construction for a 2-group? Its Lie 2-algebra will be your construction as the paper. I’m sure I’ve seen you write this before, but I can’t recall where. I can write down $E Γ$ for a general groupoid, but I can’t figure out its categorification before I go home tonight. ;D

Posted by: David Roberts on May 11, 2007 8:32 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Just above proposition 5 you mention $INN (G)$ and I just realised that it is the groupoid version of $E G$ , namely the realisation of it is Milnor’s universal bundle.

Yes. $INN (G)$ is the strict 2-group coming from the Lie crossed module $id : G \to G .$ Since that is equivalent to the trivial 2-group, the realization of its nerve is a contractible space, and indeed one finds that $\begin{matrix} ∣ (G \overset{Id}{\to} G) ∣ & ≃ & E G \\ ↓ \\ ∣ Σ G ∣ & ≃ & B G \end{matrix}$ is the universal $G$ -bundle.

For a general crossed module $(H \to G)$ one finds that the realization of the nerve, as a category, of the corresponding 2-group $∣ (H \to G) ∣$ is the classifying space of “ $H$ -bibundles relative to $G$ ” (you know what I mean, everybody has another name for these).

That was noticed at least by Branislav Jurčo in math.DG/0510078.

what is the corresponding construction for a 2-group?

All I know is that for any 2-grpup $G_{(2)}$ we canonically have the 3-group $AUT (G_{(2)})$ which has a sub-3-group $INN (G_{(3)})$ .

Whether and how this, however, generalizes the relation to classifying spaces above I don’t know.

Posted by: urs on May 11, 2007 10:43 AM | Permalink | Reply to this

Universal principal 2-bundles

$MathML-enabled post (click for more details).$

Above I mentioned in parts the following fact:

for every group $G$ , with $Disc (G)$ the discrete category over the underlying set of $G$ and with $Σ G$ the 1-object groupoid coming from $G$ , we have an “exact” sequence of categories $Disc (G) \to INN (G) \to Σ G$ (this is one of these points where it really pays to distinguish $G$ from $Σ G$ ).

The important thing is that

$INN (G)$ is equivalent to the trivial 2-group, as one easily checks (using that it’s a codiscrete groupoid).

clearly the preimage of any morphism under the projection $INN (G) \to Σ G$ is nothing but one copy of $G$ . In other words: $G$ acts freely and transitively on the fibers of $INN (G)$ under this projection.

As we mentioned above, taking nerves and realizing these geometrically, this sequence becomes the fibration which is the universal $G$ -bundle $\overset{∣ \cdot ∣}{\mapsto} (G \to E G \to B G) .$

That $INN (G)$ is trivializable translates into $E G$ being contractible.

The $G$ -action translates into the principal $G$ -action on $E G$ .

Now, behind the scenes David Roberts has started working out for simplicial groups what the analog statement of that would be, when we start with the simplicial group coming from a strict 2-group $G_{(2)}$ .

But without getting into the details of that, it is already easy to check, using the explicit description of $INN (G_{(2)})$ given here, that we do get an exact sequence of 2-categories

$Disc (G_{(2)}) \to INN (G_{(2)}) \to Σ G_{(2)} .$

Again, one finds that $INN (G_{(2)})$ is equivalent to the trivial 3-group.

So it’s pretty clear what’s going on: taking (Duskin-, I guess) nerves of this sequence and geometrically realizing, we should get the universal $G_{(2)}$ -2-bundle!

It’s natural to conjecture that this remains true for arbitrary $n$ -groups, analogously:

the universal principal $G_{(n)}$ - $n$ -bundle should be

$∣ INN (G_{(n)}) ∣ \to (∣ Σ G_{(n)} ∣ : = B G_{(n)})$

Posted by: urs on June 11, 2007 9:19 PM | Permalink | Reply to this

Re: Universal principal 2-bundles

For ordinary principal G-bundles,
being universal in the sense of classifying
is equivalent to having total space contractible. Is it known/written somewhere
that the same is true for the universal
G(2)-2-bundle?

Posted by: jim stasheff on June 12, 2007 12:54 AM | Permalink | Reply to this

Re: Universal principal 2-bundles

$MathML-enabled post (click for more details).$

For ordinary principal $G$ -bundles, being universal in the sense of classifying is equivalent to having total space contractible. Is it known/written somewhere that the same is true for the universal $G_{(2)}$ -2-bundle?

Hm, good question. I was simply assuming this would be true. But I don’t know!

But maybe if we run through the argument which tells us that $E G$ is any contractible space with a principal $G$ -action, we’ll understand why this must be true for 2-groups, too.

How does that argument go?

Posted by: urs on June 12, 2007 10:16 AM | Permalink | Reply to this

Re: Universal principal 2-bundles

$MathML-enabled post (click for more details).$

For compact Lie groups, they find $n$ large enough to inject into $U (n)$ . Then they construct $E U (n)$ here.

Is there a suitable candidate for compact Lie 2-groups?

Is there not a recipe to construct $E G$ for any group $G$ ?

Posted by: David Corfield on June 12, 2007 11:14 AM | Permalink | Reply to this

Re: Universal principal 2-bundles

$MathML-enabled post (click for more details).$

Is there not a recipe to construct $E G$ for any group G?

Yes, that was my starting point above:

for any $G$ , the universal $G$ -bundle $E G \to B G$ is $∣ INN (G) ∣ \to ∣ Σ G ∣ .$

I am thinking that this generalizes to 2-groups. To check this, I was mimicking the proof which shows that the above is indeed the universal bundle.

That proof uses the fact that the $E G$ is, up to homotopy, any contractible space with a principal $G$ action.

So all we need to show is that $∣ INN (G) ∣$ is contractible and has a principal $G$ action.

But that’s easy to see, as I described above.

And it’s just as easy to see, actually (once we have the explicit description of $INN (G_{(2)})$ , at least, that took some work (straightforward, though) to write down), that the same still holds true for $G$ replaced by a strict 2-group.

So somehow we want to geometrically realize the nerve of $INN (G_{(2)}) \to Σ G_{(2)}$ and regard that as the universal $G_{(2)}$ -bundle.

I guess above I already made a mistake in thinking about turning this entirely into a space by taking the Duskin nerve and realizing that.

That might be one way to go (realizing 2-bundles by 1-bundles with the same classification), but maybe here it’s better to realize this only partially, such that we do indeed get a universal 2-bundle (a category, etc.)

It looks like we may have to take the nerve of the 3-group $INN (G_{(2)})$ (a 2-category) ony at top level, such as to retain a 1-category. That would then be our universal 2-bundle.

Oh well. I guess probably in the end David Roberts’ way to proceed here is the best one: do everything in the world of simplicial groups.

Posted by: urs on June 12, 2007 11:29 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

David,
You’re quick - or else the current version is more transparent. I struggled for quite a while at the wrong aspects
before recognizing inn as contractible;
in fact, generated by a mapping cone.
Then I finally recalled that for a connected group, inner automorphisms are homtopic to the identity.

As for EG, see also the section on the Weil algebra - which predates Milnor’s construction.

jim

Posted by: jim stasheff on May 12, 2007 2:42 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Well I’m trying at present to figure the integrated version of $inn (g_{2})$ , mashing it with Urs’ description of $INN (G_{2})$ here.

Posted by: David Roberts on May 15, 2007 8:34 AM | Permalink | Reply to this

Re: Zoo of Lie n-Algebras

$MathML-enabled post (click for more details).$

Well I’m trying at present to figure the integrated version of $inn (𝔤_{(n)})$ , mashing it with Urs’ description of $INN (G_{2})$ here.

Yes, that’s how I found $inn (𝔤_{(2)})$ originally (though of course there is a much more immediate way to get it):

the thing is that for Lie $n$ -groups $G_{(n)}$ it is very easy to understand what the automorphism Lie $(n + 1)$ -group $AUT (G_{(n)})$ shoud be: we simply have

$AUT (G_{(n)}) : = {Aut}_{n Cat} (Σ (G_{(n)}))$ (where, as usual, I write $Σ G_{(n)}$ for the $n$ -group regarded as an $n$ -groupoid with a single object).

By differentiating this, we should obtain the derivation Lie $(n + 1)$ -algebra $DER (𝔤_{(n)}) : = Lie (AUT (G_{(n)})) .$

I am saying this, because this is an obvious construction, even though it may be tediuous to actually carry it through in concrete examples.

What is less clear to me is how given just a Lie $n$ -algebra $𝔤_{(n)}$ we would construct the Lie $(n + 1)$ -algebra $DER (𝔤_{(n)})$ directly, without first integrating everything to $n$ -groups, taking automorphisms there and then differentiating again.

(I know that Danny Stevenson has been thinkin a lot about $DER (\cdot)$ , so probably he would know how to do this.)

The same comments apply of course to inner automorphisms. There is an obvious sub Lie $(n + 1)$ -group $INN (G_{(n)}) \subset AUT (G_{(n)})$ which is that maximal sub $(n + 1)$ -group whose objects come from conjugating $k$ -morphisms in $G_{(n)}$ with objects in $G_{(n)}$ .

Accordingly, there is then the corresponding Lie $(n + 1)$ -algebra $inn (𝔤_{(n)}) : = Lie (INN (G_{(n)})) .$

For $n = 1$ this is clear. In that document I tried to compute this for $n = 2$ and $G_{(2)}$ any strict 2-group.

So, first I computed $INN (G_{(2)})$ . Then $Lie (INN (G_{(2)}))$ .

For the latter step, I use a trick: we know that

- Lie $n$ -algebras $𝔤_{(n)}$ are the same as quasi-free differential graded commutative algebras (qfDGCAs)

- and that the equations specifying the differentials of these algebras can be read off directly from the curvature $p$ -forms of an $n$ -connection with values in $𝔤_{(n)}$ .

So what I actually did (around p. 9) was that I computed the $p$ -form curvatures of a 3-connection with values in the 3-group $INN (G_{(2)})$ .

If the strict 2-group $G_{(2)}$ comes from the crossed module $(t : H \to G)$ , one finds that these connections are given by

A 1-form $A \in Ω^{1} (X, Lie (G))$ .

A 2-form $B \in Ω^{2} (X, Lie (H))$ .

A curvature 2-form $β = F_{A} + t_{*} \circ B .$

A curvature 3-form $H = d_{A} B .$ Satisfying the Bianchi identities $d_{A} β = t_{*} \circ H$ and $d_{A} H + β \land B = 0 .$ When one knows how it works (and we describe it in our Zoo) then one can directly read off the qfDGCA from these relations. That qfDGCA is (by canonical equivalence) our Lie 3-algebra $inn (𝔤_{(2)})$ .

That’s how I computed it originally.

Then, a while ago, I realized that, in the examples where I understand it ( $n = 1,2$ ) there is apparently a simple mechanism which reads in any Lie $n$ -algebra and spits out a Lie $(n + 1)$ -algebra which – in the cases that I checked – is the inner derivation Lie $(n + 1)$ -algebra of the former.

This construction is the $∞$ -functor $inn (\cdot) : n Lie \to (n + 1) Lie$ which is described in section 3.3.

This explicit construction at the level of Lie $n$ -algebras also makes clear why taking $inn (\cdot)$ is related to non-vanishing curvatures:

If the Lie $n$ -algebra $𝔤_{(n)}$ is built on a graded vector space $sV$ , then its inner derivation Lie $(n + 1)$ -algebra $inn (𝔤_{(n)})$ is built on $(sV) \oplus (ssV),$ where $ssV$ is just another copy of $sV$ , but with the degree shifted up by one.

One then sees that for every degree of $sV$ the connection will send the corresponding curvature to the corresponding degree in $ssV$ .

One finds this phenomenon already in ordinary Deligne cohomology, which corresponds to the Lie $n$ -algebra $Lie (Σ^{n} U (1))$ : there one has to truncate the complex one is working with one below top level – otherwise all curvatures would have to vanish.

From the general perspective, this is actually a trick that allows the curvature component which would really have to live in $ssV$ to be non-vanishing, simply by killing off everything.

This trick only works since $Lie (Σ^{n} U (1))$ is nontrivial only in top degree. All the lower degrees give rise to a hierarchy of “fake curvatures” ( $(p \leq n)$ -form curvatures). To deal with these – and to allow them to be nonvanishing – we need to make room for them by adding $ssV$ to our complexes.

Posted by: urs on May 15, 2007 10:37 AM | Permalink | Reply to this

some progress

$MathML-enabled post (click for more details).$

It seems that we could close two of the “open problems”.

It seems it could be shown that qfDGCAs, their morphisms and derivation homotopies of these in fact form an $(∞,1)$ -category $ω Lie .$ Moreover, the construction of the inner derivation Lie $(n + 1)$ -algebra from a given Lie $n$ -algebra extends to an $∞$ functor $inn (\cdot) : ω Lie \to ω Lie .$ This is such that in particular from $𝔤_{k} ≃ {string}_{k} (𝔤)$ it follows that $inn (𝔤_{k}) ≃ inn ({string}_{k} (𝔤)) .$ With that result in hand it suddenly became clear what to do about the expected but unproven equivalence ${cs}_{k} (𝔤) ≃ inn ({string}_{k} (𝔤))$ :

simply check if $inn (𝔤_{k}) ≃ {cs}_{k} (𝔤) .$ And that turns out to be an easy computation.

Posted by: urs on May 14, 2007 3:33 PM | Permalink | Reply to this

Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

It turns out that there is not just the 1-parameter family of Chern-Simons Lie 3-algebras, ${cs}_{k} (𝔤)$ for any semisimple Lie algebra $𝔤$ , but there are actually two infinite families of (one-parameter) Chern-Simons Lie $(2 n + 1)$ -algebras, for all odd $n$ .

One is defined for $𝔤$ any matrix Lie algebra. The Lie $(2 n + 1)$ -algebra ${cs}_{k}^{n} (𝔤)$ is characterized by the fact that connections taking values in it ar in bijective correspondence with differential forms $(A, B, C) \in Ω^{1} (X, 𝔤) \times Ω^{2 n} (X) \times Ω^{(2 n + 1)} (X)$ such that $C = d B + k {CS}_{n} (A),$ where ${CS}_{n} (X)$ is the $n$ th Chern-Simons form of $A$ .

So the $(2 n + 2)$ -form curvature of these connections is $d C = k Tr ((F_{A})^{n + 1}) .$

The other infinite family is for abelian, but higher form Chern-Simons functionals.

The Lie $(2 n + 1)$ -algebras ${cs}_{k} (Σ^{n} 𝔲 (1))$ are characterized by the fact that connections taking values in them are in bijective correspondence with differential forms $(A, C) \in Ω^{n} (X) \times Ω^{(2 n + 1)} (X)$ such that $C = d B + k A \land dA .$

This is the Lie $n$ -algebra incarnation of the objects of interest in central extensions of Deligne cohomology groups and in the latest work by Freed, Moore and Segal on abelian charged $(2 n + 1)$ -branes, aka abelian charged $(2 n + 2)$ -particles.

These families of Chern-Simons Lie $(2 n + 1)$ -algebras are now the content of section 2.4 and section 9.

Posted by: urs on May 16, 2007 4:43 PM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

This must be related to what Alissa and I did. We classified all Lie $n$ -algebras with a Lie algebra $L$ as objects and a representation $V$ of $L$ as $(n - 1)$ morphisms, in terms of the Lie algebra cohomology group

$H^{n + 1} (L, V) .$

In particular, when $L = Lie (G)$ with $G$ compact connected semisimple, and $V = ℝ$ is the trivial representation, these cohomology groups are just the same as the cohomology groups of the Lie group $G$ regarded as a space. These cohomology groups are well-known — you can look them up in tables (see page 11 here). So, we get a bunch of Lie $n$ -algebras.

For example, for $G = SU (k)$ , we have

$H^{n + 1} (Lie (G), ℝ) = ℝ$

when $n = 2, 4, 6, \dots, 2 k - 2$ and

$H^{n + 1} (Lie (G), ℝ) = 0$

otherwise. So we get a 1-parameter family of interesting Lie $n$ -algebras with $su (k)$ as 0-chains and $ℝ$ as $(n - 1)$ -chains precisely for $n = 2,4,6, \dots, 2 k - 2$ .

I don’t completely understand/remember how you’re defining ${cs}_{k}^{n} (g)$ , but since the Lie algebra cocycles I’m talking about are closely related to the Chern-Simons forms you’re describing, I’m sure your Lie 3-algebras, 5-algebras, etc. are closely related to the Lie 2-algebras, 4-algebras etc. that I’m talking about, at least in the case where $G = SU (k)$ — but in fact more generally. I’m only using $SU (k)$ as an example.

But, the interesting stuff happens when we hit Lie algebras that have characteristic classes that are not coming from the formulas you give; then we’ll get other Lie $n$ -algebras.

Posted by: John Baez on May 17, 2007 2:32 AM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

This must be related to what Alissa and I did.

Last night, when jogging along the river, I realized that these higher Chern-Simons Lie $n$ -algebras that I talked about are probably all equivalent to the inns of the Lie algebras that you mention!

Just like what I found for the ordinary Chern-Simons Lie 3-algebra: it’s the $inn$ of the Baez-Crans Lie 2-algebra $𝔤_{k}$ : ${cs}_{k} (𝔤) ≃ inn (𝔤_{k}) .$

I will work that out now and write it up.

I don’t completely understand/remember how you’re defining ${cs}_{k}^{n} (𝔤)$

The implicit definition is: this is the Lie $(2 n + 1)$ -algebra which is such that morphisms $f : Vect (X) \to {cs}_{k}^{n} (𝔤)$ are in bijective correspondence with differential forms $(A, B, C) \in Ω^{1} (X, 𝔤) \times Ω^{2 n} (X) \times Ω^{2 n + 1} (X)$ such that $C = d B + k {CS}_{n} (A) .$

Posted by: urs on May 17, 2007 11:05 AM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

I will work that out now and write it up.

I think I could check this. Actually an easy computation.

For $𝔤$ any matrix Lie algebra and an $ℝ$ -valued $(2 n + 1)$ -cocycle on that obtained by forming the trace over the product of $2 n + 1$ elements and then multiplying by a constant $k$ , let $𝔤_{k}^{n}$ be the corresponding Lie $2 n$ -algebra. Then we have an equivalence (even an isomorphism) of Lie $(2 n + 1)$ -algebras $inn (𝔤_{k}^{n}) ≃ {cs}_{k}^{n} (𝔤) .$

Clearly, this suggests a more general relation still to be identified. It looks roughly like $inn (\cdot)$ takes us from the fourth to the third column in that table on p. 11, which you mentioned, in some sense.

Posted by: urs on May 17, 2007 4:19 PM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

Clearly, this suggests a more general relation still to be identified. It looks roughly like $inn (\cdot)$ takes us from the fourth to the third column in that table on p. 11, which you mentioned, in some sense.

Yes, I think I could now get the general statement:

as we know, there is a Baez-Crans Lie $n$ -algebra $𝔤_{μ}$ for every $(n + 1)$ -cocycle $μ$ on $g$ .

Moreover, for every symmetric invariant polynomial $k$ of degree $(n + 1)$ on $𝔤$ satisfying a certain condition, we get a Lie $(2 n + 1)$ -algebra ${cs}_{k} (𝔤) .$ This is completely characterized by the fact that a connection taking values in it is a triple $(A, B, C) \in Ω^{1} (X, 𝔤) \times Ω^{2 n} (X) \times Ω^{2 n + 1} (X)$ of differential forms such that $C = d B + {CS}_{k} (A),$ where ${CS}_{k} (A)$ is defined by the invariant polynomial $k$ by $d {CS}_{k} (A) = k (F_{A} \land \dots \land F_{A}) .$

Writing $μ_{k}$ for the $(2 n + 1)$ -cocycle which is defined by $k$ , we have the following equivalence of Lie $(2 n + 1)$ -algebras (which is even an isomorphism): $inn (𝔤_{μ_{k}}) ≃ {cs}_{k} (𝔤) .$

(More details in section 10.)

In words:

Every Chern-Simons Lie $(2 n + 1)$ -algebra is (equivalent to) an inner derivation Lie $(2 n + 1)$ -algebra of a Baez-Crans Lie $2 n$ -algebra.

This gives us then a categorified and generalized version of the Stolz-Teichner statement that “string connections trivialize Chern-Simons theory”. We have, more generally:

General $(2 n + 1)$ -dimensional Chern-Simons theories are trivialized by Baez-Crans $2 n$ -connections.

Posted by: urs on May 17, 2007 7:31 PM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

While the above is right, when you think further about it you’ll realize something is funny here. Alas, I was disrupted by having to sleep a little and now by having to teach a little. Hope to get back here soon with some more clarifications.

Posted by: urs on May 18, 2007 7:32 AM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

Here are some more refinements of the above observations, in particular addressing John’s concern that nothing beyond Baez-Crans type Lie $n$ -algebras is appearing here.

As was emphasized a lot already, to every Lie algebra $n + 1$ -cocycle $μ$ on $𝔤$ we obtain a Baez-Crans Lie $n$ -algebra $𝔤_{μ}$ concentrated in degree 1 and $n$ .

I am claiming that, in a generalization of that from $𝔤$ to $inn (𝔤)$ we obtain for every degree $n + 1$ symmetric invariant polynomial $k$ on $𝔤$ a Lie $(2 n + 1)$ -algebra ${ch}_{k} (𝔤)$ concentrated in degree 1,2 and $2 n + 1$ .

I believe that these are not equivalent, in general, to any $𝔤_{μ}$ .

I call these ${ch}_{k} (𝔤)$ for Chern. They are like the Chern-Simons Lie $(2 n + 1)$ -algebras that I kept talking about, only that the latter has more entries in more degrees.

The Chern-Simons Lie $2 n + 1$ -algebra exists when the $2 n + 1$ cochain $μ_{k}$ defined by the inavriant polynomial $k$ is a cocycle, and when $k$ is trivial with respect to the cohomology of $inn (𝔤)$ (which doesn’t mean that it is trivial in the ordinary sense). (All this is described in more detail in section 10 now, cleaner than what I had before, I think ).

The Chern-Simons Lie $(2 n + 1)$ -algebra ${cs}_{k} (𝔤)$ is isomorphic (even) to the inner derivation Lie $(2 n + 1)$ -algebra of the corresponding Baez-Crans Lie $2 n$ -algebra $inn (𝔤_{μ_{k}}) ≃ {cs}_{k} (𝔤) .$ There is now a general proof included (section 3.3) that $inn (𝔤_{(n)})$ is always trivializable., for all Lie $n$ -algebras $𝔤_{(n)}$ .

So this means that the Chern-Simons Lie $(2 n + 1)$ -algebra always is trivializable as well! – which is why I said above that something funny is going on.

But it all makes sense:

we have a canonical epimorphism ${cs}_{k} (𝔤) \to {ch}_{k} (𝔤)$ which extracts the nontrivial information, namely the Chern-class coming from $k$ – in the sense that when you consider connections into these beasts, this epimorphism extracts their $(2 n + 2)$ -form curvature $d C = k ((F_{A})^{n + 1}) .$

The picture we get is this:

Posted by: urs on May 18, 2007 5:55 PM | Permalink | Reply to this

Re: Chern-Simons Lie (2n+1)-algebras

$MathML-enabled post (click for more details).$

Excellent stuff, Urs!

I think that two well-known theorems shed some light on what’s going on.

Suppose $G$ is a compact simply-connected simple Lie group and $g$ is its Lie algebra.

On the one hand we have:

Chern–Weil Theorem: If $B G$ is the classifying space of $G$ , the cohomology ring

$H^{*} (B G, ℝ),$

is isomorphic to the algebra of invariant polynomials on $g$ . Elements of this cohomology ring are called characteristic classes for $G$ .

More precisely, any homogeneous invariant polynomial of degree $n$ on $g$ corresponds to an element of $H^{2 n} (B G, ℝ)$ .

Furthermore, $H^{*} (B G, ℝ)$ is isomorphic to a polynomial algebra on finitely many generators $x_{i}$ of even degree.

There’s a ‘trangression’ map

$trans : H^{n} (B G, ℝ) \to H^{n - 1} (G, ℝ)$

and there’s an isomorphism

$H^{n - 1} (G, ℝ) ≅ H^{n - 1} (g, ℝ)$

where the left side is the cohomology of the space $G$ , but the right side is Lie algebra cohomology.

On the other hand, we have:

Theorem: The cohomology ring

$H^{*} (G, ℝ) ≅ H^{*} (g, ℝ)$

is isomorphic to an exterior algebra on the elements $trans (x_{i})$ , which are of odd degree.

On the one hand, according to what you say, each element of $H^{2 n} (B G, ℝ)$ gives a ‘Chern’ Lie $(2 n - 1)$ -algebra.

On the other hand, each element of $H^{2 n - 1} (G, ℝ)$ gives a ‘Baez–Crans’ Lie $(2 n - 2)$ -algebra.

In particular, each element $x_{i}$ of degree $n$ spawns a Lie $(2 n - 1)$ -algebra — but also, via its transgression $trans (x_{i})$ , a Lie $(2 n - 2)$ -algebra!

I hope I have the numbers right here. The ‘classic’ example, the one we know best, is supposed to be $n = 2$ . Here we get a Baez–Crans Lie 2-algebra and a Chern Lie 3-algebra. In this case, the relevant invariant homogeneous polynomial on $g$ has degree 2. It’s often called the 2nd Chern class:

$c_{2} = tr (x^{2}) .$

Note that the transgression map

$trans : H^{n} (B G, ℝ) \to H^{n - 1} (G, ℝ)$

kills a lot of stuff. For example, while

$c_{2}^{2} \neq 0$

for $G = SU (k)$ when $k$ is big enough, we always have

$trans (c_{2}^{2}) = 0$

since the cohomology of $B G$ is a polynomial algebra, while the cohomology of $G$ is an exterior algebra.

So, unless I’m confused, there are a lot more interesting ‘Chern’ Lie $(2 n - 1)$ -algebras than ‘Baez–Crans’ ones.

I think the only elements transgression doesn’t kill are linear combinations of the generators $x_{i}$ . For $SU (k)$ these generators are just the Chern classes $c_{1}, c_{2}, \dots, c_{k}$ . For other simple Lie algebras, you can see the degrees of the generators in that table on page 11 here.

Needless to say, Stasheff knows a lot about this stuff: together with Milnor, he wrote the book on characteristic classes!

Posted by:

The n-Category Café

Skip to the Main Content

May 10, 2007