Octonions and the Standard Model (Part 8)
Posted by John Baez
Last time I described the symmetry group of the exceptional Jordan algebra in terms of 10d Minkowski spacetime. We saw that in some sense it consists of four parts:
- the double cover of the Lorentz group in 10 dimensions,
- translations in left-handed spinor directions,
- translations in right-handed spinor directions, and
- ‘dilations’ (rescalings).
But our treatment was computational: the geometrical meaning of this decomposition was left obscure. As Atiyah said:
Algebra is the offer made by the devil to the mathematician. The devil says: I will give you this powerful machine, it will answer any question you like. All you need to do is give me your soul: give up geometry and you will have this marvellous machine.
Now let’s renounce the devil’s bargain and try to understand the geometry! Jordan algebras are deeply connected to projective geometry and the exceptional Jordan algebra is all about the octonionic projective plane.
Let’s start with a baby example: instead of the exceptional Jordan algebra of self-adjoint octonionic matrices, , let’s look at the Jordan algebra of self-adjoint complex matrices:
The determinant makes this into a copy of 4d Minkowski spacetime:
Any nonzero self-adjoint matrix with determinant zero spans a ‘light ray’ — a line through the origin in Minkowski spacetime that describes the path of something moving at the speed of light.
If you stand at the origin of 4d Minkowski spacetime — which in fact is exactly where you are — the set of light rays passing through you form a 2-sphere. This is the sphere of things you could see if you could freely turn your head in every direction. It’s often called the ‘heavenly sphere’, since it’s the starry sky surrounding you when you’re floating in outer space.
As you turn your head your view gets rotated — and if you’re moving, your view is Lorentz transformed, with the stars in front of you bunching up, though this effect is only noticeable if you’re moving at close to the speed of light. So, special relativity gives an action of the Lorentz group on the heavenly sphere.
But the heavenly sphere is a copy of the Riemann sphere, — and the identity component of the Lorentz group acts as conformal transformations of . These transformations form the group . So, we get an isomorphism
We can see this in more detail as follows. As I’ve mentioned, any nonzero matrix in with determinant zero yields a light ray through the origin. But any nonzero vector gives such a matrix:
So it gives such a light ray! Indeed, we get all such light rays in this manner. But multiplying by an invertible complex number just rescales , so it doesn’t change the light ray. So the set of light rays through the origin is .
Pursuing this further, we can see how acts on nonzero vectors , and thus acts on the heavenly sphere .
Now, let us use these ideas to break the group into four pieces, analogous to the four pieces of that we worked out last time. This is not hard.
The heavenly sphere can be seen as together with a point at infinity:
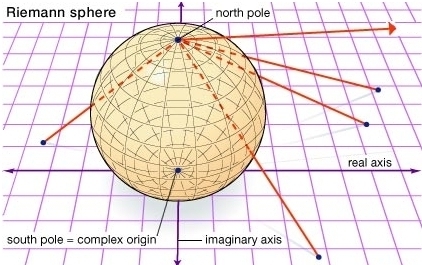
Then:
Rotations about the origin in form a subgroup of isomorphic to . These transformations preserve the origin and the point at infinity.
Translations in form an abelian subgroup of isomorphic to . These transformations preserve the point at infinity.
The point at infinity is the origin of an ‘antipodal’ copy of in the heavenly sphere, and translations in this copy of form another abelian subgroup of , also isomorphic to . These transformations preserve the origin.
Dilations of the original copy of also act as dilations of the antipodal copy of . These form an abelian subgroup isomorphic to . These transformations preserve the origin and the point at infinity.
At the Lie algebra level this gives
This is an isomorphism of vector spaces, not of Lie algebras: the four parts are Lie subalgebras, but they don’t commute with each other!
I believe that this is beautifully analogous to what we saw last time:
where again the four parts are Lie subalgebras that don’t commute with each other. This fancier version differs in two ways: we are replacing the complex numbers with the octonions, and we are replacing a 2d story with a 3d story.
Just as the group acts on , the group acts on . Just as consists of together with a point at infinity, consists of together with a ‘line at infinity’. And this let us break into four parts:
There is a subgroup of acting as linear transformations of . These preserve both the origin and the line at infinity.
Translations of form an abelian subgroup of isomorphic to . These preserve the line at infinity.
The space of lines in form a ‘dual’ copy of . Lines that miss the origin form a copy of in this dual . Translations of this other form another abelian subgroup of isomorphic to . These preserve the origin.
Dilations, i.e. rescalings of , form an abelian subgroup isomorphic to . These preserve both the origin and the line at infinity.
I need to confirm that this geometrical picture is really correct, and matches the algebraic story from last time. To match that story, one copy of should transform in the left-handed spinor representation of , while the other should transform in the right-handed spinor representation. Since the dilations commute with , their Lie algebra transforms in the trivial 1-dimensional representation of , as it should: this is the ‘scalar’ representation.
I will say more about this next time.
To flesh out the picture, it’s also important to compare two other Jordan algebras: and . Both these contain and sit inside . And both play a role in Dubois–Violette and Todorov’s description of the Standard Model gauge group, which we saw in Part 4. We met the first in Part 5: it’s 10-dimensional Minkowski spacetime! The second resembles the exceptional Jordan algebra, but without the complications arising from the octonions.
In fact we could also get the other division algebras into the act! We have Jordan algebra inclusions
where the top four are 3d, 4d, 6d and 10d Minkowski spacetime, and the bottom four are ‘exotic spacetimes’ where the determinant vanishes on a light-cone described by a cubic equation instead of a quadratic one.
These Jordan algebra inclusions give inclusions of projective geometries:
The top four are projective lines: the heavenly spheres in Minkowski spacetimes of dimensions 3, 4, 6 and 10. The bottom four are projective planes.
Each Jordan algebra has a determinant function, and a group of linear transformations preserving this determinant, so we also get these inclusions of Lie groups:
Here the two row consists of Lorentz groups, or more precisely their identity components:
Defining takes some work; I explained one approach here:
- John Baez, and Lorentzian geometry.
Defining is even harder, so we might as well just come out and say it’s , the group I’ve been talking about all along.
You may wonder where I’m going with all this. It would be easy to be seduced into endless explorations of all this math, and all the math it’s connected to, and all the math that is connected to… but I really have a specific goal in mind.
I’m trying to understand Dubois–Violette and Todorov’s description of the Standard Model gauge group in a more conceptual way. As we saw, this crucially involves picking a copy of inside , and also a copy of inside — that is, 10d Minkowski spacetime inside the exceptional Jordan algebra.
This is why, out of this big diagram:
I want to focus on this part:
and its consequences.
- Part 1. How to define octonion multiplication using complex scalars and vectors, much as quaternion multiplication can be defined using real scalars and vectors. This description requires singling out a specific unit imaginary octonion, and it shows that octonion multiplication is invariant under .
- Part 2. A more polished way to think about octonion multiplication in terms of complex scalars and vectors, and a similar-looking way to describe it using the cross product in 7 dimensions.
- Part 3. How a lepton and a quark fit together into an octonion — at least if we only consider them as representations of , the gauge group of the strong force. Proof that the symmetries of the octonions fixing an imaginary octonion form precisely the group .
- Part 4. Introducing the exceptional Jordan algebra : the self-adjoint octonionic matrices. A result of Dubois-Violette and Todorov: the symmetries of the exceptional Jordan algebra preserving their splitting into complex scalar and vector parts and preserving a copy of the adjoint octonionic matrices form precisely the Standard Model gauge group.
- Part 5. How to think of self-adjoint octonionic matrices as vectors in 10d Minkowski spacetime, and pairs of octonions as left- or right-handed spinors.
- Part 6. The linear transformations of the exceptional Jordan algebra that preserve the determinant form the exceptional Lie group . How to compute this determinant in terms of 10-dimensional spacetime geometry: that is, scalars, vectors and left-handed spinors in 10d Minkowski spacetime.
- Part 7. How to describe the Lie group using 10-dimensional spacetime geometry. This group is built from the double cover of the Lorentz group, left-handed and right-handed spinors, and scalars in 10d Minkowski spacetime.
- Part 8. A geometrical way to see how is connected to 10d spacetime, based on the octonionic projective plane.
- Part 9. Duality in projective plane geometry, and how it lets us break the Lie group into the Lorentz group, left-handed and right-handed spinors, and scalars in 10d Minkowski spacetime.
- Part 10. Jordan algebras, their symmetry groups, their invariant structures — and how they connect quantum mechanics, special relativity and projective geometry.
- Part 11. Particle physics on the spacetime given by the exceptional Jordan algebra: a summary of work with Greg Egan and John Huerta.
- Part 12. The bioctonionic projective plane and its connections to algebra, geometry and physics.

Re: Octonions and the Standard Model (Part 8)
Indeed, didn’t Faust eventually use algebra to discover his true love? And by discovering geometry, he ascended to heaven?
So it seems that there is good precedence in first using algebra to find the answer, and then using geometry to understand the answer.