Question about ∞-Colimits

August 10, 2009

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

Here is a question on a certain peculiar configuration of $(∞, 1)$ -colomits also kown as homotopy colimits, where one hocolimits is taken over another hocolimit:

Suppose $Π (X)$ is an $∞$ -groupoid and $A$ an $(∞, 1)$ -category and $F : Π (X) \to A$ is an $(∞, 1)$ -functor of which we would like to compute some push-forward, such as, for simplicity, its $(∞, 1)$ -colimit

$hocolim (Π (X) \overset{F}{\to} A) \in A .$

But let there be the following extra piece of datum: say the $∞$ -groupoid $Π (X)$ itself comes to us exhibited as a homotopy colimit in $∞$ -Grpd of a simplicial $∞$ -groupoid $Δ^{op} \to ∞ Grpd$ which I’ll denote $[Δ_{C}^{k}, X]$ for reasons to be explained below: so suppose that we have a hocolimit expression

$Π (X) ≃ {hocolim}_{k} [Δ_{C}^{k}, X] .$

This is a peculiar higher categorical situation which does not have a 1-categorical analog: we have a hocolimit over a functor $F$ out of a domain that is itself a hocolimit:

$hocolim (F) = hocolim (({hocolim}_{k} [Δ_{C}^{k}, X]) \overset{F}{\to} A) .$

Question: Are there any general useful facts one can know about such “hocolimits over hocolimits”?

In particular, let $F_{k} : [Δ_{C}^{k}, X] \to A$ be the cocone components of $F$ induced by the universality property of the colimit. Is there an expression of the hocolim over $F$ in terms of that over its components?

By looking at the relevant diagrams, one is inclined to expect that – to some maybe imperfect extent – there might be a certain commutativity rule of the sort

$\dots \overset{?}{≃} {hocolim}_{k} (hocolim ([Δ_{C}^{k}, X] \overset{F_{k}}{\to} A)),$

where now the inner holcolim is over the component functors $F_{k}$ of $F$ , and the outer hocolim is over a resulting diagram in $A$ .

Here the trouble starts with saying precisely what that diagram in $A$ formed by the ${hocolim}_{k} F_{k}$ actually is. Below is considered as one special case the case where all $F_{k}$ are constant on a single object, in which case there is a simple answer.

To see why one might expect some such “hierarchical commutativity” rule for hocolimits or similar, maybe it is helpful to contemplate the relevant diagram in low degree of $k$ , where it looks like

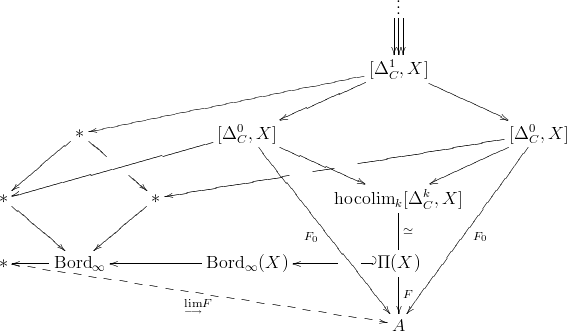
Here on the right is indicated the functor $F : Π (X) \to A$ and the way it factors into components maps as a morphism out of a hocolimit.

Then to the left is indicated how $F$ itself as well as its components maps may be pushed forward to the point, meaning that their hocolimit, denoted $\lim_{\to}$ there, are computed.

It seems from this that the colimiting cocones over the component functors $F_{k}$ want to assemble themselves to yield some kind of cocone over $F$ , much as the components $F_{k}$ themselves assemble to yield $F$ . But so far I keep getting a headache when trying to extract a precise statement along these lines.

By the way: in the above the map from $Π (X)$ to the point is factored in the curious way as indicated due to the way this question arises in the discussion of Quantization by Kan extension. More background information on that motivational aspect in the following.

$MathML-enabled post (click for more details).$

In the motivating example we are in the context of Lie $∞$ -groupoids modeled by $∞$ -stacks on $C =$ CartSp or a similar category of smooth test spaces.

Write $[-, -]$ for the internal Hom in that context.

Write $Δ_{C}^{k}$ for the standard smooth $k$ -simplex regarded as a smooth $∞$ -groupoid.

Then, in our example, we are presented with a smooth $∞$ -groupoid $X$ that plays the role of some physical space

To every such smooth $∞$ -groupoid $X$ we get the smooth $∞$ -groupoid $[Δ_{C}^{k}, X]$ of smooth $k$ -paths in $X$ . These fit together to form the smooth path $∞$ -groupoid defined by

$Π (X) : = {hocolim}_{k} [Δ_{C}^{k}, X] .$

Let now $A$ be an $(∞, n)$ -category whose underlying $∞$ -groupoid $Core (A)$ is equipped with the structure of a smooth $∞$ -groupoid. We shall abusively write $A$ for $Core (A)$ , too, when the context makes the distinction clear.

We know that morphisms

$F : Π (X) \to A$

of smooth $∞$ -groupoids characterize $∞$ -bundles with flat connection on $X$ , whose typical fiber is an equivalence class in $A$ . Sometimes one calls these $A$ -local systems on $X$ .

We want to regard one of these as the background field for a charged brane $σ$ -model and find an abstract-nonsense way to characterize the worldvolume quantum field theory as a functor on the $∞$ -category of cobordisms

$Z_{F} : {Bord}_{∞} \to A$

given the input of $F$ . Here for simplicity I take ${Bord}_{∞}$ , which should be an $∞$ -groupoid. I regard this as a smooth $∞$ -groupoid with trivial smooth structure.

There is also the mixed version ${Bord}_{∞} (X)$ of bordisms with smooth maps into $X$ . Into that $Π (X)$ should embed as the sub $∞$ -groupoid of bordisms that are topologically just disks.

Now, one may imagine several abstract-nonsense operations to get from $F$ to $Z_{F}$ .

One proposal is indicated in

Freed-Hopkins-Lurie-Teleman, Topological Quantum Field Theories from Compact Lie Groups.

It seems, but is a bit hard to tell, that essentially they are proposing for the special case of constant $F = {const}_{a}$ that for a cobordism $Σ_{in} \to Σ \leftarrow Σ_{out}$ with the induced diagram

$\begin{matrix} [Σ, X] \\ ↙ & ↘ \\ [Σ_{in}, X] & ↓^{{const}_{a}} & [Σ_{out}, X] \\ _{{const}_{a}} ↘ & ↙_{{const}_{a}} \\ A \end{matrix}$

we are to take the hocvolimit over each of the vertical constant functors

$\begin{matrix} {hocolim}_{[Σ, X]} {const}_{a} \\ ↙ & ↘ \\ {hocolim}_{[Σ_{in}, X]} {const}_{a} & {hocolim}_{[Σ_{out}, X]} {const}_{a} \end{matrix}$

and then in turn the hocolimits over the resulting diagram in $A$ to produce

${hocolim}_{k} (hololim (S_{k} \overset{{const}_{a}}{\to} A),$

where now $k$ denotes some indexing of the above diagram and $S_{k}$ denotes the objects $[Δ_{C}^{\cdot}, X]$ , just to emphasize the pattern.

They discuss how if $A$ is a suitable $∞$ -catgeory of algebras, the object thus obtained is naturally a bimodule that may be regarded as a morphism from $hocolim ([Σ_{in}, X] \overset{{const}_{a}}{\to} A)$ to $hocolim ([Σ_{in}, X] \overset{{const}_{a}}{\to} A)$

Now, there is another abstract nonsense that one may consider subjecting the functor $F$ . It looks like it leads to something similar. But I am not sure what the precise relation is. My question is, if anyone can help me see the relation between the two different double hocolim constructions presented below.

So consider the homotopy colimit over $F$ itself. Since $F$ maps out of an $∞$ -groupoid that is itself given by a homotopy colimit, it is of the form

$hocolim ({hocolim}_{k} [Δ_{C}^{k}, X] \overset{F}{\to} A) .$

So we can take the corresponding diagram apart into the components $F_{k}$ of $F$ as depicted here:

Question: what is the relation between

$hocolim (({hocolim}_{k} [Δ_{C}^{k}, X]) \overset{F}{\to} A)$

and

${hocolim}_{k} (hocolim ([Δ_{C}^{k}, X] \overset{F_{k}}{\to} A))$

Actually, as the diagram is supposed to indicate, I don’t really expect that this is quite the right question yet. More precisely one should probably ask the question not for push-forwards to the point, but for the intermediate push-forwards indicated above.

But I’ll leave it at that level of vagueness for the moment and see if anyone can help me out with a useful comment on the material as indicated so far.

Posted at August 10, 2009 8:39 PM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2033

6 Comments & 0 Trackbacks

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

This is a peculiar higher categorical situation which does not have a $1$ -categorical analog

I think it does, just not quite so circularly. I don't know anything about it, but if there is anything to be known, there should be something known about colimits over categories that are themselves $2$ -colimits in $Cat$ .

Posted by: Toby Bartels on August 10, 2009 11:16 PM | Permalink | Reply to this

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

This is a peculiar higher categorical situation which does not have a 1-categorical analog

I think it does, just not quite so circularly. I don’t know anything about it, but if there is anything to be known, there should be something known about colimits over categories that are themselves 2-colimits in Cat.

Yes, that’s what part of what I am saying: it doesn’t arise in a purely 1-categorical context, you need at least a notion of colimits over categories.

On the other hand, there may be more good 1-categorical analogs than it might seem on first sight:

the crucial fact that Charles Rezk kindly emphasizes in his comment below is that the hocolim over an $(∞, 1)$ -presheaf $F : X \to ∞ Grpd$ happens to coincide with what for 1-categorical presheaves would be its category of elements in that it is the pullback of the universal fibration of $(∞, 1)$ -categories

$Z ∣_{Grpd} \to ∞ Grpd$

whose homotopy fiber over each $C \in ∞ Grpd$ is just $C$ itself.

So we have a homotopy pullback

$\begin{matrix} hocolim F & \to & Z ∣_{Grpd} \\ ↓ & ↓ \\ X & \overset{F}{\to} & ∞ Grpd \end{matrix}$

by the theorem summarized at limit in a quasi-category.

For a 1-categorical presheaf $F : C \to Set$ we would similarly take the universal $Set$ -bundle ${Set}_{*} \to Set$ and consider the pullback

$\begin{matrix} \int F & \to & {Set}_{*} \\ ↓ & ↓ \\ X & \overset{F}{\to} & Set \end{matrix}$

which is the category of elements of $F$ .

(You, Toby, know all this, I am just saying it for completeness).

So a useful 1-categorical analog of my question should be obtained with one of the two colimit notions replaced by “pullback of universal fibration”.

Posted by: Urs Schreiber on August 11, 2009 1:29 PM | Permalink | Reply to this

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

If I understand your question correctly, I think it is exactly correct. Here is the picture that I have of it:

For me, I want to thnik of the $∞$ -groupoid $Π (X)$ as just being a space $X$ . The functor $F : X \to A$ I think of as a “bundle” of objects of $A$ over the space $X$ .

If $A$ is the $(∞, 1)$ -category of spaces, this is literally true: the functor $F$ corresponds to a fibration $E_{F} \to X$ . In this case, the homotopy colimit of $F$ is the space $E_{F}$ .

Now, I’ll suppose that $X$ is a homotopy colimit. Using simplicial homotopy colimits shouldn’t be crucial, so I’d rather take $X$ to be a homotopy colimit of a diagram of spaces $X_{1} \leftarrow X_{0} \to X_{2}$ .

The restriction of $F$ to $X_{i} \to X$ is a functor $F_{i} : X_{i} \to A$ , and so corresponds to a fibration $E_{F_{i}} \to X_{i}$ . But this fibration is exactly the homotopy pullback of $E_{F} \to X$ along $X_{i} \to X$ ; restriction of functors between $∞$ -groupoids is homotopy pullback of fibrations.

So I think your formula amounts to saying: $E_{F} = hocolim (E_{F_{1}} \leftarrow E_{F_{0}} \to E_{F_{2}}) .$ This is certainly true if $A =$ spaces (it is an instance of the “descent” property of an $(∞, 1)$ -topos).

Well, that argument assumed that $A =$ spaces. But it certainly can be extended to the case when $A$ is an $(∞, 1)$ -category of presheaves of spaces. I think you can prove your formula even if $A$ is a Bousfield localization of a presheaf $(∞, 1)$ -category, which includes almost anything you’d like. But I’m too sleepy to check it right now …

Posted by: Charles Rezk on August 11, 2009 7:13 AM | Permalink | Reply to this

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

Thanks for your reply!

If I understand your question correctly, I think it is exactly correct. […]

(it is an instance of the “descent” property of an $(\infty, 1)$ -topos)

Thanks, that was the nudge that I needed.

Okay, so let me recall the relevant facts to see if I get them straight:

First of all, it is a theorem – now recalled at limit in a quasi-category – that for $F : X \to ∞ Grpd$ an $∞$ -functor from an $∞$ -groupoid $X$ to the $(∞, 1)$ -category of $∞$ -groupoids its (homotopy) colimit is equivalent to the pullback of the universal fibration of $(∞, 1)$ -categories $Z \to (∞, 1) Cat$ along $F$ , in that

$\begin{matrix} hocolim F & \to & Z ∣_{∞ Grpd} \\ ↓ & ↓ \\ X & \overset{F}{\to} & ∞ Grpd \end{matrix}$

is a (homotopy) pullback.

Next, it is a big theorem by you – which appears as theorem 6.1.6.8 in HTT – that in a (Grothendieck-Rezk-Lurie-) $(∞, 1)$ -topos all colimits are universal (and in fact this is part of the characterization of them), which is a funny way of saying that they are stable under base change.

In particular this is true in the archetypical $(∞, 1)$ -topos $Top$ , where it should be a classical fact.

Here we use it with the above theorem to deduce the formula

$hocolim (({hocolim}_{k} C_{k}) \overset{F}{\to} D) ≃ {hocolim}_{k} (hocolim (C_{k}) \overset{F_{k}}{\to} D)$

from the fact that the pullback along the universal $(∞, 1)$ -categorical fibration $Z \to (∞, 1) Cat$ preserves colimits, so that

$\begin{matrix} hocolim F & ≃ & {hocolim}_{k} (hocolim F_{k}) & \to & Z ∣_{∞ Grpd} \\ ↓ & ↓ & ↓ \\ X & ≃ & {hocolim}_{k} X_{k} & \overset{F}{\to} & ∞ Grpd \end{matrix} .$

So that clarifies the situation in the case where the functor in question has as domain an $∞$ -groupoid and as codomain the $(∞, 1)$ -category of $∞$ -groupoids.

I think you can prove your formula even if $A$ is a Bousfield localization of a presheaf $(∞, 1)$ -category, which includes almost anything you’d like. But I’m too sleepy to check it right now…

I’d be quite grateful if you could help me with this question indeed for the case that $∞$ -Grpd in the above is replaced with some $(∞, 1)$ -category of $(∞, 1)$ -sheaves, yes.

I am somewhat puzzled about where in that case I should think of the analog of the morphism $F : X \to ∞ Grpd$ to actually live.

My other puzzlement at the moment is that for the applications that I indicated in the above entry it’s not really that the coefficient object is $∞ Grpd$ or some other $(∞, 1)$ -topos. It’s rather some incarnation of somthing that deserves to be called $n Vect$ or the like. Maybe $\Pr^{L}$ .

I’d be grateful for whatever comments you might have.

Posted by: Urs Schreiber on August 11, 2009 2:03 PM | Permalink | Reply to this

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

I have another question, this time on how to re-express hocolims over hocolims as hocolims over holims.

First, start with the setup as before. Let $C$ be a category, regarded as an $(∞, 1)$ -category, and

$H : C \to ∞ {Grpd}^{op}$

some $(∞, 1)$ -functor.

Write $X : = hocolim H$ for its colimit.

Then consider another functor $F : X \to ∞ Grpd$ and its hocolim.

As now recalled at limit in a quasi-category this yields in total a diagram of the form

$\begin{matrix} hocolim F \\ ↓ \\ X = hocolim H & \overset{F}{\to} & ∞ Grpd \\ ↓ \\ C & \overset{H}{\to} & ∞ Grpd \end{matrix},$

where the two vertical morphisms are the coCartesian fibrations arising as the pullback of the opposite of the universal fibration of $∞$ -groupoids.

Now, as recalled at these links, coCartesian fibrations of course compose to coCartesian fibrations. Therefore the vertical composite in the above diagram is a coCartesian fibration. So it must come from some classifying $(∞, 1)$ -functor

$tot : C \to ∞ Grpd$

top yield a pullback diagram

$\begin{matrix} hocolim X & \to & Z ∣_{∞ Grpd}^{op} \\ ↓ & ↓ \\ C & \overset{tot}{\to} & ∞ Grpd \end{matrix}$ Question 1: Is there a formula for $tot$ ?

By just looking at the diagram, there is an obvious guess for what $tot$ must roughly be like:

a given $c$ in $C$ it must send to the $∞$ -groupoid which is the union of all the sections of $hocolim F \to X$ over all sections of $X \to C$ over $c$ .

So we want to choose sections $σ : C \to X$ , postcompose these with $F$ and sum up the result of that.

$\begin{matrix} hocolim F \\ ↓ \\ X = hocolim H & \overset{F}{\to} & ∞ Grpd \\ ^{σ} ↗ & ↓ \\ C & \overset{=}{\to} & C & \overset{H}{\to} & ∞ Grpd \end{matrix},$

So i’d expect some sub $(∞, 1)$ -category

$Γ_{C}^{sortof} (X) \to Func (C, X)$

of the full functor category $Func (C, X)$ such that the sought for classifying morphism of the total vertical coCartesian fibration is the hocolim

$hocolim (Γ_{C}^{sortof} (X) \to Func (C, X) \overset{Func (C, F)}{\to} Func (C, ∞ Grpd)) \in Func (C, ∞ Grpd) .$

Question 2: Is there a choice for $Γ_{C}^{sortof} (X)$ such that this is true?

There is one natural candidate that comes to mind: the $(∞, 1)$ -category of cartesian sections $Γ_{C}^{cart} (X)$ of $X \to C$ .

We know that this happens to be the limit over $H$ . I thought that would help me see what happens when I feed it into the above question. But it didn’t so therefore I finally have

Question 3: What can we say about

$hocolim (Γ_{C}^{cart} (X) \to Func (C, X) \overset{Func (C, F)}{\to} Func (C, ∞ Grpd)) \in Func (C, ∞ Grpd) .$

And by now it is inevitable that I also ask

Question 4: How is all this related to the $(∞, 1)$ -categorical Kan extension (if any) of $F$ along $X \to C$ ?

Posted by: Urs Schreiber on August 13, 2009 12:17 AM | Permalink | Reply to this

Re: Question about ∞-Colimits

$MathML-enabled post (click for more details).$

I wrote:

Question 1: Is there a formula for tot?

Sorry, I realize that my question is, or should be, another one:

let

$\begin{matrix} X & \overset{F}{\to} & ∞ Grpd \\ ↓^{p} \\ B \end{matrix}$

be a diagram of $(∞, 1)$ -categories. Adjoin to this the hocolim coCartesian fibration of $F$

$\begin{matrix} hocolim F \\ ↓ \\ X & \overset{F}{\to} & ∞ Grpd \\ ↓^{p} \\ B \end{matrix}$

Now while $hocolim F \to X$ is a coCartesian fibration, the total vertical morphism $hocolim F \to X \overset{p}{\to} B$ is in general not.

So within the model structure on marked simplicial over-sets for coCartesian fibrations find a fibrant replacement $fib (hocolim F) \to B$ of $hocolim F \to B$ . This will be classified by some functor $p_{*} F : B \to ∞ Grpd$ .

Is there any kind of useful formula or other tools for determining $p_{*} F$ here?

How does $p_{*} F$ relate to an $(∞, 1)$ -categorical Kan extension (if any) of $F$ along $p$ ?

Posted by: Urs Schreiber on August 13, 2009 10:07 PM | Permalink | Reply to this

The n-Category Café

Skip to the Main Content

August 10, 2009