A Scale-Dependent Notion of Dimension for Metric Spaces (Part 1)
Posted by Simon Willerton
Consider the following shape that we are zooming into and out of. What dimension would you say it was?
At small scales (or when it is very far away) it appears as a point, so seems zero-dimensional. At bigger scales it appears to be a line, so seems one-dimensional. At even bigger scales it appears to have breadth as well as length, so seems two-dimensional. Then, finally, at very large scales it appears to be made from many widely separated points, so seems zero-dimensional again.
We arrive at an important observation:
The perceived dimension varies with the scale at which the shape is viewed.
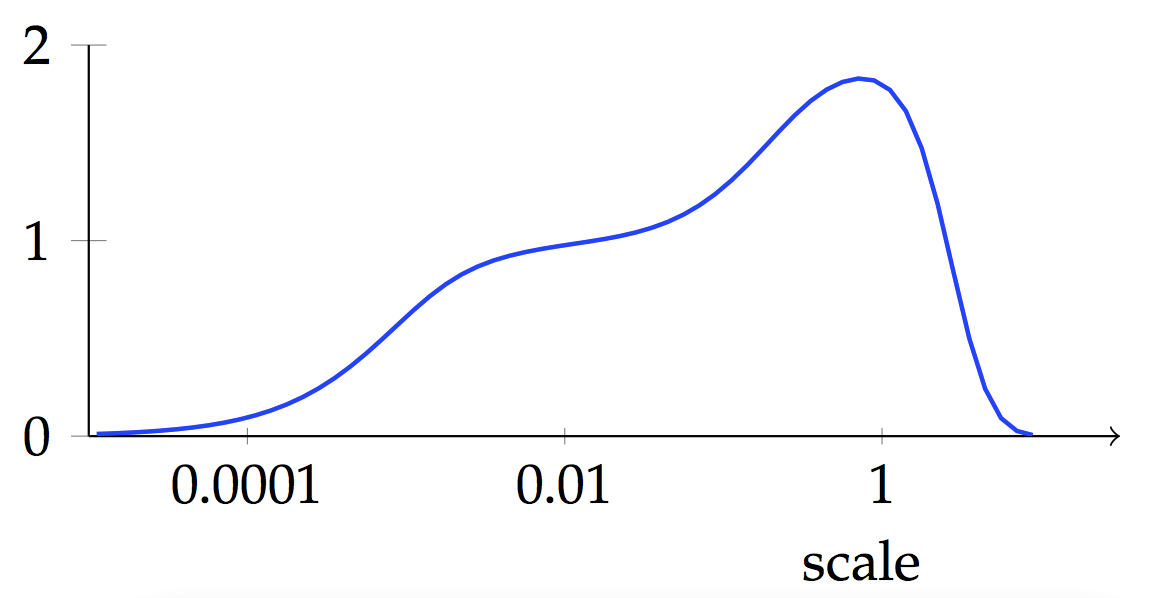
Here is a graph of my attempt to capture this perceived notion of dimension mathematically.
Hopefully you can see that, moving from the left, you start off at zero, then move into a region where the function takes value around one, then briefly moves up to two then drops down to zero again.
The ‘shape’ that we are zooming into above is actually a grid of points as that’s all my computer could handle easily in making the above picture. If I’d had a much bigger computer and used say points then I would have got something that more obviously had both a one-dimensional and two-dimensional regime.
In this post I want to explain how this idea of dimension comes about. It relies on a notion of ‘size’ of metric spaces, for instance, you could use Tom’s notion of magnitude, but the above picture uses my notion of -spread.
I have mentioned this idea before at the Café in the post on my spread paper, but I wanted to expand on it somewhat.
What do we mean by dimension?
First we should try to understand how we think of dimension. We are used to thinking of it in terms of ‘degrees of freedom’, or the number of different directions you can go in, so a line is one dimensional and a square is two dimensional. This will always give us an integer dimension.
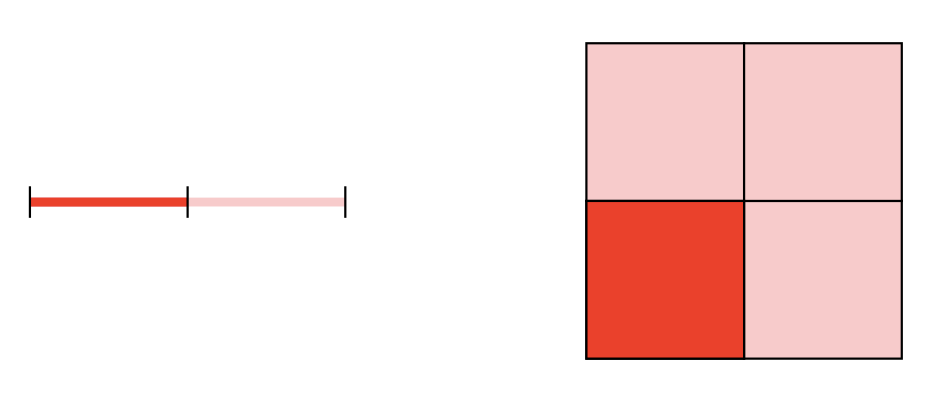
It was realised that there were spaces that could be given meaningful non-integer dimensions by using a different approach to what dimension is. Let’s follow one train of thought. If we think about the square and the line again, we can see that they have different scaling properties. If we scale up a line by a factor of two, then we can fit exactly two copies of the original line in. If we scale up a square by a factor of two then we can fit four copies of the original square in.
More generally if we scale up the line by a factor of then we can fit copies of the original line in and if we similarly scale up the square by a factor of we can fit copies of the original square. The indices and coincide with the dimensions of the spaces.
Let’s take that as the basis of a different notion of dimension and see what happens when we scale up some fractally shapes.
A first attempt at defining dimension
Let’s take a not well defined notion of scale dimension to be the following. Say that the scale dimension is if when we scale up by a factor of (for suitable ) we get copies of our original space back.
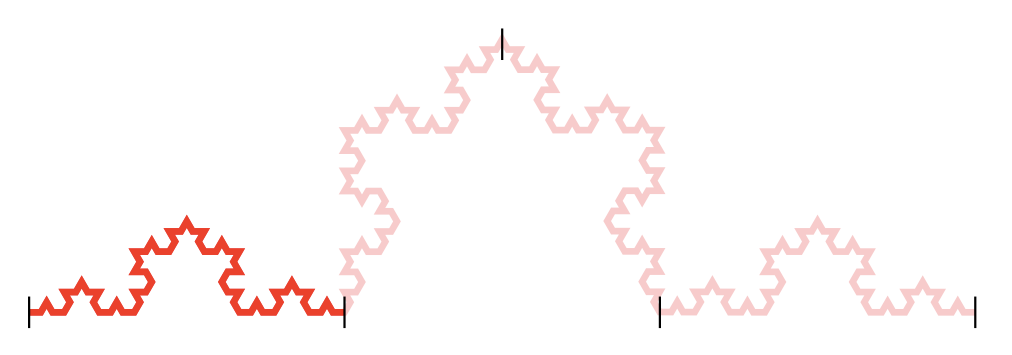
We see that the Koch curve is scaled by a factor of we can fit four copies of the original in, or more generally when scaled by a factor of we can fit copies in. So this says that the scale dimension is .
Similarly for ‘the Cantor set. If you scale it by a factor of three you can fit two copies of the original in, more generally if we scale it by a factor of we can fit copies in. So this says that the scale dimension is .
The above idea, although appealing, has several flaws. One flaw is that it is not clear what is meant by having -copies of our original shape: for instance, when we scale up the square and decompose into smaller squares the boundaries overlap, so we get a bit less than four copies. Another flaw is that the above idea only works for certain special shapes: for instance, if we scale up a disk by a factor of two we don’t get a shape we can decompose into four of our original shapes. Indeed, there is no such that when we scale up a disk by a factor of we get a shape that can be decomposed into copies of our original disk.
A second attempt
We could address these two flaws by observing that when we scale up a plane shape such as a square or a disk by a factor of two we get a shape which is four times the area of the original shape. Similarly, when we scale all lengths by a factor of we get a shape which has the area. More generally, for a shape in -dimensional Euclidean space, when we scale all lengths by a factor of we get a shape which has times the volume.
So we could try to say that a shape has volume dimension if when you scale it up by a factor of the volume changes by a factor of . Unfortunately, that doesn’t work for various reasons. Firstly, you have to specify the kind of volume you need for each shape, so you need length for lines and area for squares, so you’re presupposing the dimension when you pick the volume to use! Secondly, this is not going to work for fractals as none of these volumes make sense for a fractal. The Koch curve does not have a meaningfully non-trivial length or area. (To define fractal dimensions such as the Hausdorff or Minkowski dimension you’d take a different turn at this point, but we’ll carry on the way we’re going.)
Defining dimension using a notion of size
An alternative would be if we had a single notion of size which we could use for all shapes simultaneously. For a given shape we could then see how this size changes under scaling and use that to define a notion of dimension. This is the approach I used as I know of several appropriate notions of size.
Tom Leinster introduced ‘magnitude’ which is a notion of size which is defined for every compact subset of a Euclidean space — and more generally, for every compact, positive definite metric space. I’ll not give the definition here.
Tom also introduced ‘maximum diversity’ which is based on magnitude, is a bit more complicated to define but is somewhat better behaved on all metric spaces. He gives the definition in this post if you are interested.
I introduced a one-parameter family of notions of size which are defined for every finite metric space — and I suspect for every compact subset of Euclidean space as well. These are easier to define and calculate, but I’ll just give the definitions for and , which are particularly nice to write down. If is a finite metric space with points then the -spread and -spread are defined as follows:
Once we have a notion of size , we want to use this to define a notion of dimension which tells us how the size alters under scaling. Typically we can’t do anything as naive as finding a such that if we scale by a factor of then the size scales by a factor of , the sizes described above are generally more interesting than that!
For a shape and we define to be the shape scaled up by a factor of . We then have the size being a function of and we define the dimension of to be the growth rate of this function at . By growth rate I mean some number associated to a function such that the growth rate of is . Recalling from school that the way to calculate the growth rate of a function is to plot the function on log-log paper and measure the gradient, we take the instantaneous growth rate of a function to be the logarithmic derivative, . A couple of applications of the chain rule tell us that this is just .
For a notion of size , this leads us to define the S-dimension of a shape by
The graph in the introduction is the -dimension of the lattice of points in the animation plotted as we scale the set of points, i.e. it’s the graph of as we vary .
In practice, it seems that the magnitude, and dimensions of a given shape look very similar. They have different advantages over each over: for instance, we know, or have conjectured, closed forms for magnitudes of several shapes; but in the case of things that we don’t have a closed form for it is quicker to calculate the - or -spread dimension.
Next time…
Next time I’ll give more examples. I’ll also say something about connections with Minkowski dimension, although I don’t understand the full story there.





Re: A Scale-Dependent Notion of Dimension for Metric Spaces (Part 1)
If your growth rate graph width was scaled from 400 to 380, HTML layout wouldn’t create all that blank space and position it after the right side bar ends.