Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

March 14, 2015

Split Octonions and the Rolling Ball

Posted by John Baez

You may enjoy these webpages:

because they explain a nice example of the Erlangen Program more tersely — and I hope more simply — than before, with the help of some animations made by Geoffrey Dixon using WebGL. You can actually get a ball to roll in way that illustrates the incidence geometry associated to the exceptional Lie group G 2\mathrm{G}_2!

Abstract. Understanding exceptional Lie groups as the symmetry groups of more familiar objects is a fascinating challenge. The compact form of the smallest exceptional Lie group, G 2\mathrm{G}_2, is the symmetry group of an 8-dimensional nonassociative algebra called the octonions. However, another form of this group arises as symmetries of a simple problem in classical mechanics! The space of configurations of a ball rolling on another ball without slipping or twisting defines a manifold where the tangent space of each point is equipped with a 2-dimensional subspace describing the allowed infinitesimal motions. Under certain special conditions, the split real form of G 2\mathrm{G}_2 acts as symmetries. We can understand this using the quaternions together with an 8-dimensional algebra called the ‘split octonions’. The rolling ball picture makes the geometry associated to G 2\mathrm{G}_2 quite vivid. This is joint work with James Dolan and John Huerta, with animations created by Geoffrey Dixon.

I’m going to take this show on the road and give talks about it at Penn State, the University of York (virtually), and elsewhere. And there’s no shortage of material to read for more details. John Huerta has blogged about this work here:

* John Huerta, G2 and the rolling ball.

and I have a 5-part series where I gradually lead up to the main idea, starting with easier examples:

* John Baez, Rolling circles and balls.

There’s also plenty of actual papers:

So, enjoy!

Posted at March 14, 2015 1:18 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/2814



12 Comments & 0 Trackbacks

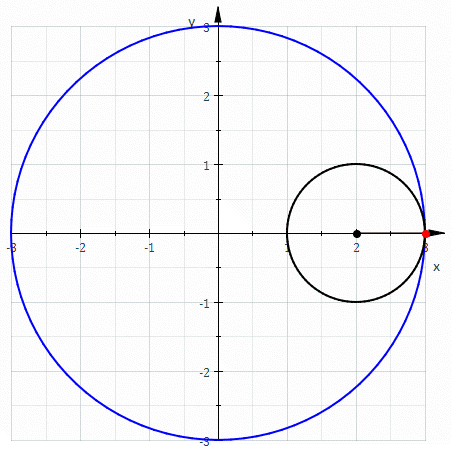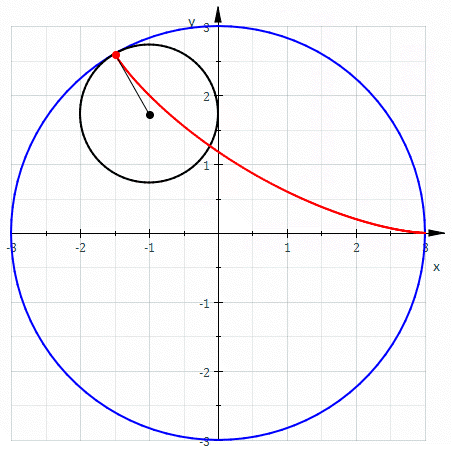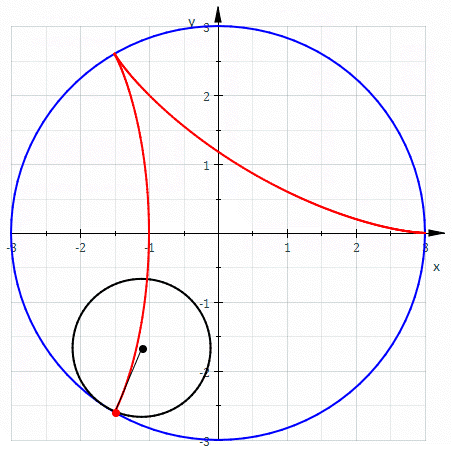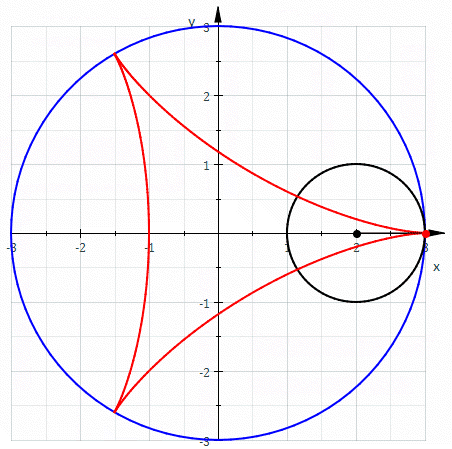
Re: Split Octonions and the Rolling Ball

Nice Demo!

Don’t forget that if the point on the small circle radius is inside the small circle, you generate an epitrochoid. You are now half-way to the Wankel Rotary Engine. Thank you Felix Wankel and thank you Bernoulli brothers.

Posted by: Charles Wilson on March 14, 2015 3:00 AM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

This particular epitrochoid is called a deltoid:

and we discussed it in Part 3 of the rolling circles and balls series. You can get a deltoid in various ways: for example, as the set of traces of matrices in SU(3).

The Wankel engine:

(Click for links.)

Posted by: John Baez on March 15, 2015 6:27 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

A tiny note for John: The rightward pointing arrow on the bottom right of http://math.ucr.edu/home/baez/rolling/rolling̲\underline{\;}3.html links to rolling̲\underline{\;}3 again, not to the next page.

Posted by: David Speyer on March 16, 2015 2:00 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

Thanks! I do these things manually and often screw up. Then I keep fixing them…

Fixed!

Posted by: John Baez on March 16, 2015 5:16 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

Just some stupid question. If we define the relative number of turns of the little sphere over the big one as the number of times one point of it crosses the normal to the big sphere in some direction, then we would notice that the small sphere does exactly 3 relative turns.

Is this concept known, and wouldn’t it be more useful? I’m wondering if its true for any relative radius.

Posted by: sure on March 18, 2015 1:10 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

I guess I’m dumb, its nothing else than the number of time a point on the little sphere hits the big one. So this gives you the number of “vertices” the red graphes you draw has.

Posted by: sure on March 18, 2015 1:14 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

As you note, that concept is known, and useful. Nonetheless the whole setup only works because a ball rolling on a ball 3 times as big turns around 4 times when measured ‘absolutely’, as compared to the ‘fixed stars’. I explain why in my slides.

Why the allusion to the ‘fixed stars’? Because the Earth sees the Sun go around 365¼ times during a year, but the stars go around 366¼ times. It’s the same effect.

Posted by: John Baez on March 18, 2015 9:31 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

Trochoidal Oil Pump Demo:

https://www.youtube.com/watch?v=Ds_SlghtImA

CW

Posted by: Charles Wilson on March 18, 2015 8:08 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

(no real need to watch a video)

Wikipedia: Gerotor

Wikipedia:Gerotor

Posted by: RodMcGuire on March 19, 2015 4:13 PM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

my question is very simple. How to create the animation? Which sofware do you use for? Thx a lot

Posted by: career finder on March 19, 2015 12:18 AM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

My question is also quite simple,

does this knowledge get us any further towards a physical/geometric description of the Octonion group (rather than the imaginary split Octonions)?

Thanks.

Posted by: Tom on March 25, 2015 4:22 AM | Permalink | Reply to this

Re: Split Octonions and the Rolling Ball

The octonions aren’t a group, they’re a nonassociative division algebra (you can add, multiply, subtract and divide them).

The ordinary octonions and split octonions are closely connected, so any way to construct the split octonions also gives a way to construct the octonions.

More technically: the octonions 𝕆\mathbb{O} and split octonions 𝕆′\mathbb{O}\prime are algebras over the real numbers; if we complexify either of them we get the bioctonions, ℂ⊗𝕆≅ℂ⊗𝕆′\mathbb{C} \otimes \mathbb{O} \cong \mathbb{C} \otimes \mathbb{O}\prime, which is an algebra over the complex numbers. They are the only algebras with this property. So, we say the octonions and split octonions are ‘real forms’ of the bioctonions. The same pattern shows up elsewhere, and it’s always the split real form that has a nice connection to incidence geometry.

Geometric quantizing classical mechanics problems gives complex Hilbert spaces. In our paper we describe how to construct the imaginary bioctonions by geometrically quantizing the rolling ball problem. Then, sitting inside here, you can find both the imaginary octonions and imaginary split octonions.

Posted by: John Baez on March 25, 2015 5:07 PM | Permalink | Reply to this

Post a New Comment