Integral Octonions (Part 5)
Posted by John Baez
I’m back from China. I saw lots of cool stuff:
(Click for more information.)
But I also had lots of time sitting in trains, buses and automobiles to think about the root polytope. Calculations along these lines turn out to be a great antidote to boredom!
So now I’d like to show you how to calculate the number of vertices, edges, 2d faces, etc. of this 8-dimensional polytope. What’s interesting is not the answers so much as the technique, which involves Dynkin diagrams.
If you take a bunch of equal-sized balls in 8 dimensions, and get as many as possible to all touch a central one, their centers will be the vertices of the root polytope. Here are two attempts to draw it—click for more information:
In its full 8-dimensional glory, this shape has:
- 240 vertices
- 6,720 edges
- 60,480 2d faces, which are all equilateral triangles
- 241,920 3d faces, which are all regular tetrahedra
- 483,840 4d faces, which are all regular 4-simplexes
- 483,840 5d faces, which are all regular 5-simplexes
- 207,360 6d faces, which are all regular 6-simplexes
- 19,440 7d faces, consisting of 17,280 regular 7-simplexes and 2,160 regular 7-orthoplexes
and
- a symmetry group with 696,729,600 elements, including rotations and reflections.
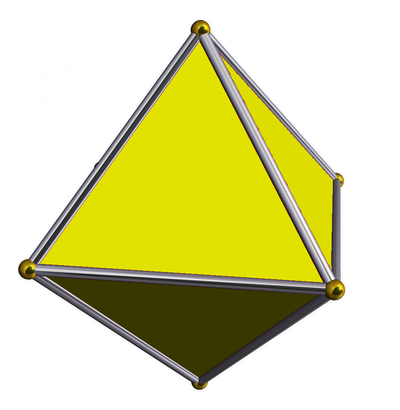
Remember, a 3-simplex is a tetrahedron:

while a 3-orthoplex is an octahedron:
Anyone can look up these crazy numbers on Wikipedia. But how can we see that they’re right?
That’s our challenge for today. It’s easiest if we define the root polytope starting from this picture:
and use the theory of simply-laced Dynkin diagrams, which are Dynkin diagrams without any multiple edges between dots. (Most of what I’m about to say generalizes to other Dynkin diagrams, but I’ll save a bit of time by focusing on this case.)
Suppose we’ve got such a diagram with dots. At an elementary level, this diagram tells us to take a bunch of unit vectors in -dimensional Euclidean space, and make sure they lie at a angle if there’s no edge connecting them, and a angle if there is an edge connecting them.
We get a lattice called the root lattice by taking all integer linear combinations of these vectors. The nonzero vectors closest to the origin are called roots. These roots are the vertices of an -dimensional convex polytope called the root polytope.
The roots include the vectors we started with, one for each dot in our Dynkin diagram: these are called the simple roots. But there are also a lot more.
Starting with the Dynkin diagram, we can in principle figure out everything we want to know about the root polytope, including how many faces of each dimension it has, and the size of its symmetry group. But to do such things elegantly, it helps to use some tricks.
Coxeter groups
The main trick is to use the theory of Coxeter groups. Any simply-laced Dynkin diagram gives such a group, and it’s very easy to describe. It has one generator obeying
for each dot in the Dynkin diagram, one relation
for each pair of dots connected by an edge, and one relation
for each pair of dots not connected by an edge. Each generator corresponds to a reflection: the reflection that flips the th simple root to its negative.
For example, starting with the Dynkin diagram called :
we get a group with 3 generators, which happens to be the symmetry group of a regular tetrahedron:

So, you should think of the three dots in the Dynkin diagram as standing for ‘vertex’, ‘edge’ and ‘face’. Why? Because the corresponding generators of the Coxeter group are reflections that:
• switch two neighboring vertices,
• switch two neighboring edges, and
• switch two neigboring faces,
respectively!
The diagram gives the symmetry group of a regular -simplex in just the same way. A similar story applies to the symmetry group of the regular -dimensional orthoplex, but the Dynkin diagram for this is not simply laced, so I won’t get into the details. The cases we really need now are the Dynkin diagram and the sub-diagrams of this.
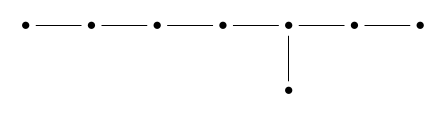
For example, if we pull off the end dot of we get a sub-diagram called , which looks like this:
or, after prettying it up, this:
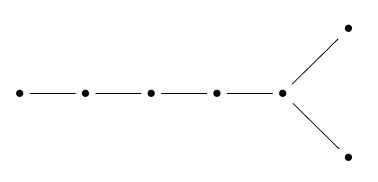
Reading from left to right, can think of the dots here as standing for ‘vertex’, ‘edge’, ‘2d face’, ‘3d face’ and so on… but when we get to the right end of the diagram, obviously something funny must happen!
There are two dots that mean ‘top-dimensional face’. The reason is that this Coxeter group is the symmetry group of a 7-orthoplex that has its 6-dimensional faces colored alternately white and black. We only consider symmetries that carry faces to faces of the same color. Two 6d faces intersect in at most one 5d face, so there’s no dot for ‘5d face’. We can summarize the story like this:

All the Dynkin diagrams look similar, with some number of dots in a row followed by two at the end… and they all work the same way. Their Coxeter groups are the symmetry groups of orthoplexes with their top-dimensional faces colored alternately white and black.
In the case of , something even stranger happens! The top-dimensional faces are of two kinds: 7-simplex and 7-orthoplex:
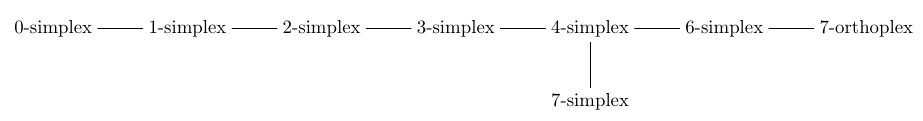
Other subtleties arise for the sub-diagrams and . So, you’re probably thinking that this subject is an elaborate quagmire. But it’s not.
Coxeter complexes
To deal with all Coxeter groups in a systematic way, it’s better to think of them as symmetry groups of certain simplicial complexes called ‘Coxeter complexes’. Roughly speaking, a simplicial complex is a gadget made of 0-simplexes, 1-simplexes, 2-simplexes, 3-simplexes, and so on — all stuck together in a nice way.
If you have a Coxeter diagram with dots, the highest dimension of the simplexes in its Coxeter complex is . There is one of these top-dimensional simplexes for each element of the Coxeter group. For example, I’ve already said this Dynkin diagram:

gives the Coxeter group consisting of symmetries of a regular tetrahedron — by which I mean all reflections and rotations. This group has 4! = 24 elements, so the Coxeter complex is built from 24 triangles. And in fact, we get it by barycentrically subdividing the surface of a tetrahedron! We can draw it on a sphere, like this:

You can see there are 24 triangles. And, you can see that if you fix a given triangle, there’s a unique symmetry of the Coxeter group mapping it to any other triangle.
In general, the Coxeter group of a Dynkin diagram with dots always acts as linear transformations of . Each root gives a reflection that flips that root to its negative. So, this group also acts on the -sphere. If we take this sphere and chop it up along the hyperplanes corresponding to all the reflections in the Coxeter group, we get the Coxeter complex. See if you can visualize this in the picture above.
Even better, if you pick any top-dimensional simplex in the Coxeter complex, there always exactly one element of the Coxeter group that maps it to any other top-dimensional simplex. So the Coxeter complex is the best possible thing made out of simplexes on which the Coxeter group acts as symmetries!
The size of the Coxeter group corresponding to a Dynkin diagram is always the product of some integers, one for each dot in the Dynkin diagram. These integers have lots of important properties, and calculating them is really the key to all the problems we’ve set out to solve. To start with, let me just show you these numbers and what we can do with them.
Here they are. For any Dynkin diagram , let be its Coxeter group, also known as its Weyl group. Here are the sizes of these groups for all the simply-laced Dynkin diagrams:
It’s easy to see that , the symmetry group of the -dimensional simplex, has size equal to
since the -simplex has symmetries permuting its vertices any way you want. While it’s not a simply-laced example, it’s also easy to see that , the symmetry group of the -dimensional orthoplex, has size equal to
This number is equal to the double factorial
Finally, it’s also easy to see that , the symmetry group of the orthoplex with its top-dimensional faces colored alternately white and black, is half as big. So, its size is the half double factorial of :
So, the only problem is computing the size of , , and . I’ll talk about this later.
You might think it’s somewhat arbitrary how we wrote the size of these Coxeter groups as products of numbers—but it’s not! I’ll talk about this more at the end of the article. But here’s a little taste of the fun:
Puzzle 1. If you double each of these numbers and subtract one, then add up the results, you get the dimension of the Lie group corresponding to this Dynkin diagram. Why?
Let’s check that it works for :
Yes, this is the dimension of the Lie group !
Getting ready to calculate
Assuming we know the size of the Coxeter groups for all the simply-laced Dynkin diagrams, let’s see if we can calculate how many faces of each kind the root polytope has.
I explained the method in week187. Each Dynkin diagram describes a kind of ‘incidence geometry’ with different kinds of figures—points, edges, triangles, tetrahedra and so on—one for each dot in the Dynkin diagram. These figures can be ‘incident’ to each other—e.g., a triangle can lie on a tetrahedron—and there’s one basic incidence relation for each edge in the Dynkin diagram.
The Coxeter group acts transitively on the figures of any given kind. We can also work out the subgroup of that preserves a figure of a given kind. To do this, we just remove the corresponding dot from the Dynkin diagram, and get a sub-diagram . Then is the subgroup we want!
So, the set of the figures of a given kind is . Thus, the number of figures of this kind is the ratio
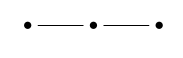
To see if you understand this, let’s do an easy example! How many edges does a tetrahedron have? Here our Dynkin diagram is :

It describes a geometry, namely a tetrahedron, with figures of three kinds:
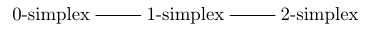
Suppose we want to count the number of 1-simplexes, or edges. We take the ‘1-simplex’ dot:

and we remove it, obtaining this sub-diagram:

Hmm, this isn’t connected! But that’s okay. This diagram is the disjoint union of two copies of the one-dot Dynkin diagram, . If you follow the rules, you’ll see its Coxeter group is the product
So, the number of edges in a tetrahedron is
which is right!
If you’ve never done this sort of stuff, I encourage you to play around with more examples. It’s lots of fun! But having spent years warming up with exercises like that, I’m now going to climb Mount Everest and count the various figures in the root polytope.
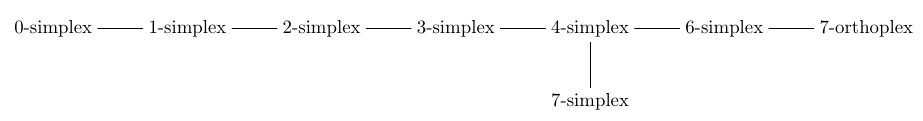
It starts out easy, but near the end, as you might imagine from this picture, it gets tricky—and I’ll slip and fall. Hanging from a icy cliff, I’ll ask for your help!
0-simplexes
If we remove the ‘vertex’ dot from the Dynkin diagram:

we’re left with :

So, the number of vertices of the root polytope is
as we knew!
Just for fun, in the next to last step I cancelled all the numbers I could from the big fraction in the top line. This is worth doing because a -deformed version of the same calculation lets us count the number of points in a certain space called a ‘Grassmannian’ for the version of the group defined over the finite field with elements, where is any prime power. I explained how this works in week186 and week187.
In the -deformed count we replace integers with -integers, defined as follows:
So, for this particular Grassmannian the number of points is
or, doing all the cancellations we can,
This, believe it or not, is a polynomial in . But we can’t say it’s equal to , because in general . Only when we set does this equation hold, and then we get 240 points. So, our problem now, involving Coxeter groups, concerns the special case of the legendary but so far still mythical ‘field with one element’.
But if we wanted, we could look at the group defined over the field with 2 elements. It acts in a transitive way on a set with
points. How many points is that? In this case
so the number of points is
1-simplexes
If we remove the ‘edge’ dot from the Dynkin diagram:
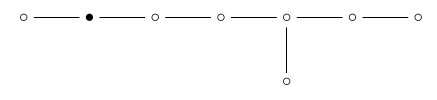
we’re left with :
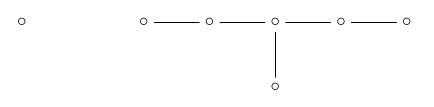
So, the number of edges of the root polytope is
2-simplexes

A 2-simplex is just a triangle. If we remove the ‘2-simplex’ dot:
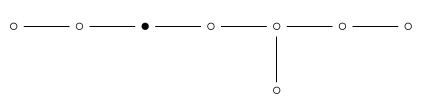
we’re left with :
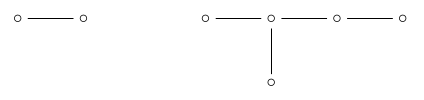
so the number of 2d faces is
3-simplexes

This is a funny picture of a 3-simplex, or tetrahedron. If we remove the ‘3-simplex’ dot:
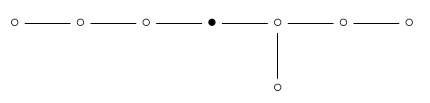
we’re left with :

so the number of 3d faces is
4-simplexes

This is a picture of a 4-simplex. If we remove the ‘4-simplex’ dot from the Dynkin diagram:
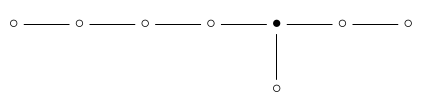
we’re left with :
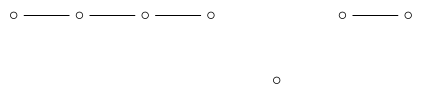
so the number of 4d faces is
5-simplexes

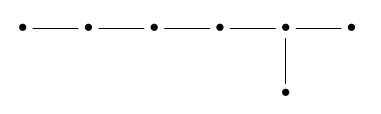
At this point we meet a mystery: there is no ‘5-simplex’ dot in the Dynkin diagram!
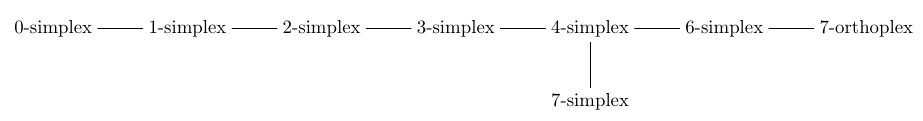
This is a bit like how there is no 5-simplex dot in the Dynkin diagram:

The resolution there is that if we have ‘complete flag’ consisting of one figure of each kind shown in this picture, all incident, there is a unique 5-simplex that’s incident to all the other figures. Indeed, there’s at most one 5-simplex touching any pair consisting of a white and a black 6-simplex. So, the 5-simplex is ‘redundant’.
The same sort of resolution must, I think, apply to . Understanding this in detail would make a good test of our understanding. But let’s move on!
6-simplexes

If we remove the ‘6-simplex’ dot:
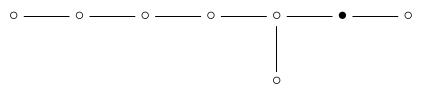
we’re left with :
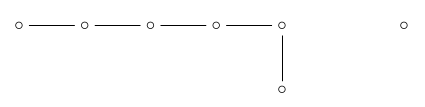
so the number of 6d faces is apparently:
But this does not agree with Wikipedia’s answer! It says our polytope has 207,360 6-dimensional faces, which are all regular 6-simplexes. So, we have another mystery on our hands here, which we will return to.
7-simplexes

If we remove the ‘7-simplex’ dot:
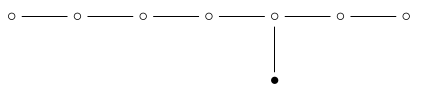
we are left with :
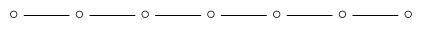
so the number of 7-dimensional simplex faces is:
7-orthoplexes

If we remove the ‘7-orthoplex’ dot:
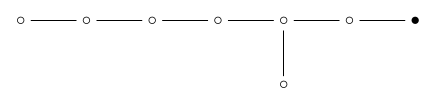
we are left with :
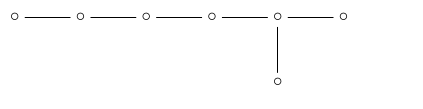
so the number of 7-dimensional orthoplex faces is:
Further mysteries
We’ve got some mysteries to solve.
6-simplexes
First, our calculations seemed to show the number of 6-simplex faces of root polytope of is 69,120, while Wikipedia says the answer is 207,360. Luckily we can compute the answer another way, which sheds a little light on this problem.
Our polytope has 17,280 7-simplex faces and 2,160 7-orthoplex faces. Each 7-simplex has 8 faces, all of which are 6-simplexes. Each 7-orthoplex has 27 faces, all of which are 6-simplexes. So, we could naively count the total number of 6-simplexes and get
But this is double-counting, since each 6-simplex touches two 7-simplexes. (The top-dimensional faces of a convex polytope always meet in pairs along faces of the next highest dimension.) So the real count is half this:
This matches the answer on Wikipedia. But it also sheds some light on our wrong answer. Our wrong answer, 69,120, is exactly the total number of faces of all the 7-simplexes. It’s also half the total number of faces of the 7-orthoplexes. It’s also exactly 1/3 of the correct answer!
All this suggests that the 6-simplex faces of our polytope come in two kinds, which cannot be interchanged by symmetries of the polytope. 1/3 of them are the ones we counted, the kind mentioned in this diagram:
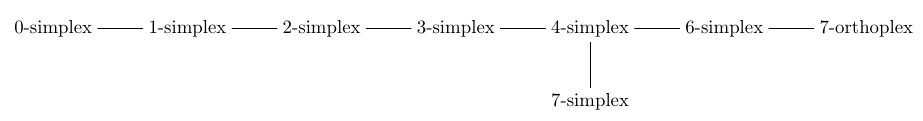
2/3 of them are 6-simplexes of some other kind, which do not appear in the above diagram.
If this seems weird, remember that this diagram also does not include the 5-simplex faces of our polytope! Also remember that the diagram, corresponding to the 7-orthoplex, gives another example where some simplexes come in two kinds, while others do not appear at all, even though they exist as faces of the 7-orthoplex:

Even if this is true, it’s clearly not enough for a full understanding. If our polytope has two kinds of 6-simplex as faces, how do they differ? And where is the number 1/3 coming from?
Here’s my guess. The 7-orthoplex faces of our polytope have 6-simplex faces that can be colored alternately white and black, and all the symmetries of our polytope preserve this two-coloring. As evidence, note that the symmetries preserving a 7-orthoplex form the group , which preserves such a two-coloring. But I’m guessing we can do this two-coloring in a consistent way, so every 6-simplex in our polytope is either white or black.
And I’m guessing we can do this so that each 7-orthoplex touches another 7-orthoplex on each of its black faces, and a 7-simplex on each of its white faces! On the other hand, every 7-simplex is completely surrounded by 7-orthoplexes.
If we can do this:
• Each white 6-simplex is the face of a unique 7-simplex, so the number of white 6-simplexes is
These are the 6-simplexes we counted.
• Each white 6-simplex is the face of a unique 7-orthoplex, so the number of white 6-simplexes is also
where we get a factor of because only half the 6-simplex faces of each 7-orthoplex are white. This is a consistency check!
• Each black 6-simplex is the face of two 7-orthoplexes, so the number of black 6-simplexes is
• The total number of 6-simplexes is
as it says on Wikipedia.
All this fits together nicely… so while I haven’t proved the existence of this ‘consistent two-coloring’ and this arrangement of 6-simplexes and 6-orthoplexes, I believe it.
Puzzle 2. Prove or disprove my guesses here!
5-simplexes
Why does our polytope have 483,840 5d faces, which are all regular 5-simplexes? I haven’t figured out how to count them. With work I should be able to do it using my guesses in the previous section, but I made these guess just a few minutes ago.
Notably, 483,840 is also the number of 4d faces.
Puzzle 3. Show how to count the 5d faces of the root polytope.
The magic numbers
All my calculations rely on general results that I understand, together with some numbers:
In fact for my calculations I only need to know the sizes of these three Coxeter groups, but it’s irresistible to try understanding the ‘magic numbers’ that you can multiply to get their sizes.
Puzzle 4. What’s the best way to calculate these magic numbers?
Back in week186 and week187 I gave many characterizations of these magic numbers. Unfortunately, they don’t seem to make it easy to calculate these numbers for and .
I bet somebody knows an easy way. But to help you with this puzzle, I’ll tell you eight hard ways!
Start with any Dynkin diagram , not necessarily simply-laced. Let be the corresponding simple algebraic group over a field . In particular,
is a complex Lie group. Suppose the diagram has dots. Then the magic numbers are natural numbers such that
Moreover:
1) The real cohomology of is an exterior algebra on generators , one for each dot of the Dynkin diagram. The degrees of these generators are all odd, and the degree of is .
2) The real cohomology of the classifying space is a polynomial algebra on generators . The degrees of these generators are all even, and the degree of is .
3) The Weyl group acts on . The algebra of polynomials on invariant under this group action is a free commutative algebra on generators . The polynomial is homogeneous of degree .
4) Define the q-polynomial of the Dynkin diagram to be the polynomial in where the coefficient of is the number of -cells in the Bruhat decomposition of the flag variety . Here is the Borel subgroup of , and the Bruhat decomposition is a standard way of writing as disjoint union of -cells, that is, copies of . Then the -polynomial equals
where .
5) If the coefficient of in the -polynomial is , the th homology group of is
6) The value of the -polynomial when is a prime power is the cardinality of . Here is the field with elements, and is the Borel subgroup of the simple algebraic group .
7) The coefficient of in the -polynomial is the number of Coxeter group elements of length . Here the length of any element in the Coxeter group is its minimal length as a word when we write it as product of the generators corresponding to dots in the Dynkin diagram.
8) The coefficient of in the polynomial is the number of top-dimensional simplexes of distance from a chosen top-dimensional simplex in the Coxeter complex. Here we measure ‘distance’ between top-dimensional simplexes in the hopefully obvious way, based on how many walls you need to cross to get from one to the other.
If you know enough stuff you may have fun proving all these descriptions of the magic numbers are equivalent.
I have not managed to use any of these descriptions of the magic numbers to solve this problem:
Puzzle 5. Why is these sequence of magic numbers for any Dynkin diagram ‘symmetrical’?
To explain what I mean here, look at the pattern of spacings between magic numbers for :
It doesn’t change when you reflect it! The same is true for and also the non-exceptional cases if you write the magic numbers in increasing order. Why? It’s reminiscent of Poincaré duality, but I don’t see how it is that.
Puzzles 1 and 5 could be clues for Puzzle 4.











Re: Integral Octonions (Part 5)
I’ll need to think about it more, but I’m pretty sure that (1) the symmetry is more evident for the magic numbers minus 1, and (2) they’re the exponents appearing in the eigenvalues of the Coxeter element. Then the symmetry comes from that guy being an orthogonal transformation of Lie(T).
There’s a lot more numerology about these exponents/degrees, and the place to read it is gray Humphreys (“Reflection groups and Coxeter groups”), which I don’t have with me.