Quasicrystals and the Riemann Hypothesis
Posted by John Baez
Freeman Dyson is a famous physicist who has also dabbled in number theory quite productively. If some random dude said the Riemann Hypothesis was connected to quasicrystals, I’d probably dismiss him as a crank. But when Dyson says this, it’s a lot more interesting. So I’ve been trying to understand his remarks on this. And it’s been productive, in that I’ve learned some interesting things, and I now feel closer to seeing why the Riemann Hypothesis is a natural and important conjecture.
But still, I could use a lot of help: I don’t have much time for number theory, and a few pointers from experts could keep me from going down dead ends.
Those of you who were using the internet around 1990 may remember newsgroups like sci.math, sci.physics, sci.math.research and sci.physics.research. That’s how internet-savvy mathematicians and physicists communicated back then. And if you were around then, you may remember Matt McIrvin, who wrote consistently intelligent and good-natured posts about physics.
I lost track of him for a while, but met him again on Google+, where has been using the open-source math software called Sage to play around with ideas from number theory.
Sage comes equipped with a table of nontrivial zeros of the Riemann zeta function computed by Andrew Odlyzko. Remember, this function is given by
when , but it can be analytically continued over the whole complex plane except for a pole at 1, and then it turns out that for a lot of points on a line:
where is a real number. Here are the first few:
The Riemann Hypothesis claims that all the zeros of the zeta function lie on this line, except for the so-called trivial zeros at and so on. Riemann only checked this for the first three cases… but by now people have checked it for the first 10,000,000,000,000 cases. So it seems to be true, but nobody can prove it.
The nontrivial zeros of the Riemann zeta function are really interesting. There’s no simple formula for them, but they encode information about prime numbers. Riemann was the first to notice this… but Matt ran into it on his own.
He took the first ten thousand positive numbers that make
and he added up a bunch of functions like this:
one for each .
The result is a function of , and he graphed its absolute value. The graph has lots of sharp spikes!
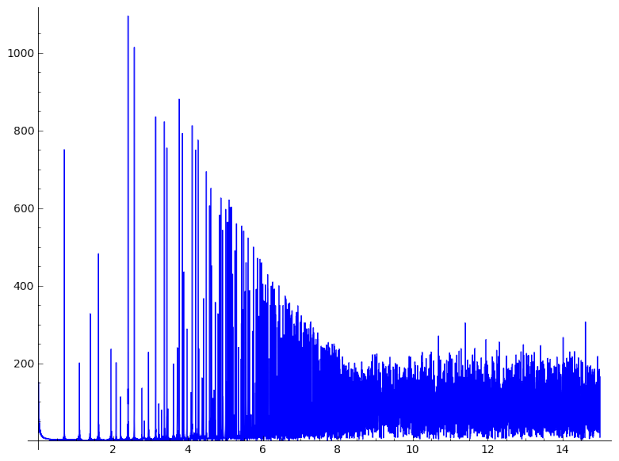
And where are these spikes? He zoomed in on the first few:
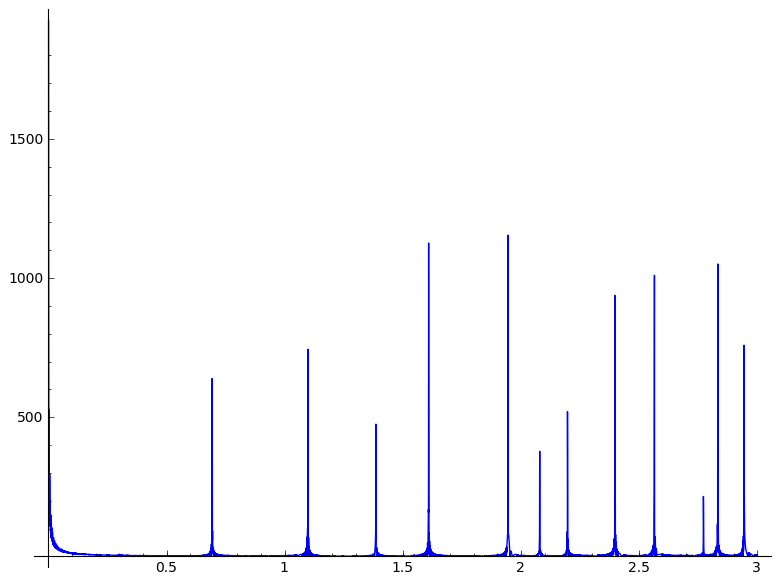
He wrote:
A closeup of those first spikes. I wonder what those numbers are, exactly? Probably they’re in the literature somewhere.
I looked around and soon found that those spikes should be here:
See the pattern?
Dyson’s remarks
In math jargon, what Matt did is take the Fourier transform of a sum of Dirac deltas supported at the imaginary parts of the nontrivial Riemann zeta zeros. The answer seemed to be another sum of Dirac deltas, times different numbers: the different spikes in the pictures above seem to have different heights. It’s unusual to take the Fourier transform of such a spiky function and get another spiky function. And according to Freeman Dyson, this is the defining feature of a quasicrystal!
When I was looking around for clues, one of the first things I ran into was a lecture by Dyson. He never actually delivered this lecture—it was cancelled at the last minute for some reason—but it was printed here:
- Freeman Dyson, Frogs and birds, Notices of the American Mathematical Society 56 (2009), 212–223.
It was about two styles of doing mathematics, hence the curious title. He said:
The proof of the Riemann Hypothesis is a worthy goal, and it is not for us to ask whether we can reach it. I will give you some hints describing how it might be achieved. Here I will be giving voice to the mathematician that I was fifty years ago before I became a physicist. I will talk first about the Riemann Hypothesis and then about quasicrystals.
There were until recently two supreme unsolved problems in the world of pure mathematics, the proof of Fermat’s Last Theorem and the proof of the Riemann Hypothesis. Twelve years ago, my Princeton colleague Andrew Wiles polished off Fermat’s Last Theorem, and only the Riemann Hypothesis remains. Wiles’ proof of the Fermat Theorem was not just a technical stunt. It required the discovery and exploration of a new field of mathematical ideas, far wider and more consequential than the Fermat Theorem itself. It is likely that any proof of the Riemann Hypothesis will likewise lead to a deeper understanding of many diverse areas of mathematics and perhaps of physics too. Riemann’s zeta-function, and other zeta-functions similar to it, appear ubiquitously in number theory, in the theory of dynamical systems, in geometry, in function theory, and in physics. The zeta-function stands at a junction where paths lead in many directions. A proof of the hypothesis will illuminate all the connections. Like every serious student of pure mathematics, when I was young I had dreams of proving the Riemann Hypothesis. I had some vague ideas that I thought might lead to a proof. In recent years, after the discovery of quasicrystals, my ideas became a little less vague. I offer them here for the consideration of any young mathematician who has ambitions to win a Fields Medal.
Quasicrystals can exist in spaces of one, two, or three dimensions. From the point of view of physics, the three-dimensional quasicrystals are the most interesting, since they inhabit our three-dimensional world and can be studied experimentally. From the point of view of a mathematician, one-dimensional quasicrystals are much more interesting than two-dimensional or three-dimensional quasicrystals because they exist in far greater variety. The mathematical definition of a quasicrystal is as follows. A quasicrystal is a distribution of discrete point masses whose Fourier transform is a distribution of discrete point frequencies. Or to say it more briefly, a quasicrystal is a pure point distribution that has a pure point spectrum. This definition includes as a special case the ordinary crystals, which are periodic distributions with periodic spectra.
Excluding the ordinary crystals, quasicrystals in three dimensions come in very limited variety, all of them associated with the icosahedral group. The two-dimensional quasicrystals are more numerous, roughly one distinct type associated with each regular polygon in a plane. The two-dimensional quasicrystal with pentagonal symmetry is the famous Penrose tiling of the plane.
Finally, the one-dimensional quasicrystals have a far richer structure since they are not tied to any rotational symmetries. So far as I know, no complete enumeration of one-dimensional quasicrystals exists. It is known that a unique quasicrystal exists corresponding to every Pisot–Vijayaraghavan number or PV number. A PV number is a real algebraic integer, a root of a polynomial equation with integer coefficients, such that all the other roots have absolute value less than one [1]. The set of all PV numbers is infinite and has a remarkable topological structure. The set of all one-dimensional quasicrystals has a structure at least as rich as the set of all PV numbers and probably much richer. We do not know for sure, but it is likely that a huge universe of one-dimensional quasicrystals not associated with PV numbers is waiting to be discovered.
Here comes the connection of the one-dimensional quasicrystals with the Riemann Hypothesis. If the Riemann Hypothesis is true, then the zeros of the zeta-function form a one-dimensional quasicrystal according to the definition. They constitute a distribution of point masses on a straight line, and their Fourier transform is likewise a distribution of point masses, one at each of the logarithms of ordinary prime numbers and prime-power numbers. My friend Andrew Odlyzko has published a beautiful computer calculation of the Fourier transform of the zeta-function zeros [2]. The calculation shows precisely the expected structure of the Fourier transform, with a sharp discontinuity at every logarithm of a prime or prime-power number and nowhere else.
My suggestion is the following. Let us pretend that we do not know that the Riemann Hypothesis is true. Let us tackle the problem from the other end. Let us try to obtain a complete enumeration and classification of one-dimensional quasicrystals. That is to say, we enumerate and classify all point distributions that have a discrete point spectrum […] We shall then find the well-known quasicrystals associated with PV numbers, and also a whole universe of other quasicrystals, known and unknown. Among the multitude of other quasicrystals we search for one corresponding to the Riemann zeta-function and one corresponding to each of the other zeta-functions that resemble the Riemann zeta-function. Suppose that we find one of the quasicrystals in our enumeration with properties that identify it with the zeros of the Riemann zeta-function. Then we have proved the Riemann Hypothesis and we can wait for the telephone call announcing the award of the Fields Medal.
These are of course idle dreams. The problem of classifying one-dimensional quasicrystals is horrendously difficult, probably at least as difficult as the problems that Andrew Wiles took seven years to explore. But if we take a Baconian point of view, the history of mathematics is a history of horrendously difficult problems being solved by young people too ignorant to know that they were impossible. The classification of quasicrystals is a worthy goal, and might even turn out to be achievable.
[1] M. J. Bertin et al., Pisot and Salem Numbers, Birkhäuser, Boston, 1992.
[2] A. M. Odlyzko, Primes, quantum chaos and computers, in Number Theory: Proceedings of a Symposium, 4 May 1989, Washington, DC, USA (National Research Council, 1990), pp. 35–46.
Questions
I wanted to understand this better, so I asked around on Mathoverflow. I got a lot of help. For starters, I got pointed to some critical remarks by Nick S., who said:
Well his definition of quasicrystals is not the one used by the quasicrystal community (we actually don’t have a formal mathematical definition yet)…. His statement about icosahedral group is false, actually most 3-dimensional models don’t have any symmetry group. Same issue for the 2 dimensional quasicrystals, most of them are not related to polygons in the plane. […] I really have no idea what he mean by “it is well known that a unique quasicrystal exists corresponding to every PV number”. The existence is true, the uniqueness is far for true… Unless I’m making a terrible mistake, there are constructions which produce pure point diffractive sets from PV numbers, and they produce uncountably many… In many situations, but not always, one can probably get that most of them are “equivalent” in some sense, but not all of them… And the big issue is that any equivalence in this sense, unless one adds very strong extra conditions, allows for .. small translations of the points… And there are of course uncountably many models which are not associated to PV numbers. Another issue is that the zeroes of the RZF are not a Delone set, so anything done so far by the quasicrystal community is not relevant to the problem… And last, I really don’t see how one can go around the following issue: Let be the set of zeroes. Let be the set obtained by moving all the zeroes, such that the th zero is moved by at most . Then diffraction cannot differentiate between and .
I don’t know if these remarks are true, so if any of you know, please tell me… preferably with references!
I don’t care too much if Dyson is using ‘quasicrystal’ in a nonstandard sense. He at least seems to be hinting at a fairly precise definition, perhaps “a countable sum of Dirac deltas on that defines a tempered distribution whose Fourier transform is a countable linear combination of Dirac deltas”. The phrase ‘defines a tempered distribution’ just means the Dirac deltas don’t bunch up too fast, so the Fourier transform is well-defined. Allowing the original sum to also be a more general linear combination of Dirac deltas might be be nice, too: then the Fourier transform of a quasicrystal would be another quasicrystal!
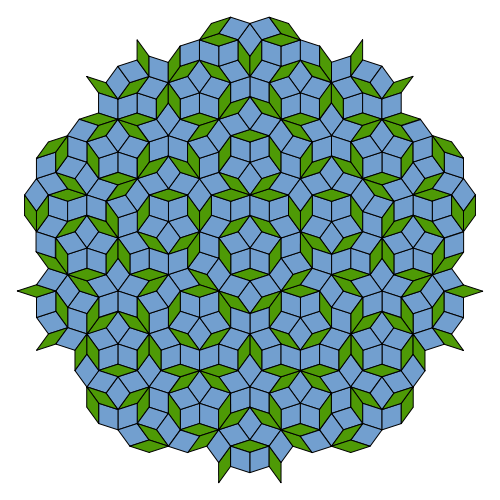
Anyway, what I’d like to learn is what’s known about such entities. In what sense, if any, does any Pisot–Vijayaraghavan number give a unique quasicrystal in 1 dimension? Do de Bruijn’s quasiperiodic tilings, like this one drawn by Greg Egan’s software, give quasicrystals in Dyson’s sense?
Is it really true that all quasicrystals in 3 dimensions are related to the icosahedral group? What’s the theorem there? And what about the 4-dimensional pattern built from the E8 lattice—is that a quasicrystal in Dyson’s sense? Is it hard to find higher-dimensional quasicrystals, or easy?
The Guinand–Weil explicit formula
But now I’d like to come to my actual point, which concerns this remark:
If the Riemann Hypothesis is true, then the zeros of the zeta-function form a one-dimensional quasicrystal according to the definition. They constitute a distribution of point masses on a straight line, and their Fourier transform is likewise a distribution of point masses, one at each of the logarithms of ordinary prime numbers and prime-power numbers.
Is this actually true? In other words, does the Riemann Hypothesis actually imply this? And if so, why?
At first I thought it was true. That would make a very nice bumper sticker explaining the ‘meaning’ of the Riemann Hypothesis… something like
RIEMANN ZETA ZEROS ARE FOURIER DUAL TO LOGS OF PRIME POWERS!
This is the first version of the Riemann Hypothesis I’ve seen that makes me really want it to be true. You can see it discussed in this excellent book draft here, with lots of pretty pictures:
- Barry Mazur and Richard Stein, Primes.
But it seems the truth is a bit more complicated. The truth is called the explicit formula of Guinand and Weil and it involves terms, not only for the nontrivial zeros of the zeta function, but also for the trivial zeros, and the pole. And in fact it’s best to think of this formula not in terms of the original Riemann zeta function, but the ‘corrected’ version that takes the ‘prime at infinity’ into account using the gamma function, namely:
This ‘corrected’ version has the all-important symmetry:
that lets you see the zeros of this function, and thus all the nontrivial zeros of the original Riemann zeta function, lie in the strip .
So, I still have hope for getting a conceptually clear statement of the Riemann Hypothesis that’s exactly correct! However, so far, I can’t seem to say something correct without it looking rather messy. For example, on Mathoverflow Brad Rogers stated a version of the Guinand–Weil explicit formula that looks about like this:
For a compactly supported smooth function with Fourier transform ,
Here the sum is over such that is a non-trivial zero of the Riemann zeta function. is the Chebyshev prime counting function:
and
Alas, this formula doesn’t look very ‘conceptual’, though I think I’m beginning to understand it, and Marc Palm gave a nice sketch of a proof.
In this formula, can be complex if the Riemann Hypothesis is false. But if it’s true, is always real, and the left-hand side of the big equation
is really just the test function integrated against a sum of complex exponentials, one for each nontrivial zero of the zeta function. (I should warn you that these zeros come in complex conjugate pairs, so for each positive real we get a corresponding negative ).
The right-hand side of the big equation contains a ‘nice’ term that’s a sum over prime powers, but also some ‘corrections’ that seem to make Dyson’s claim fail to be literally true. For example, besides a linear combination of Dirac deltas at logarithms of prime powers, there’s the correction term proportional to the function . Owen Maresh has plotted this function:
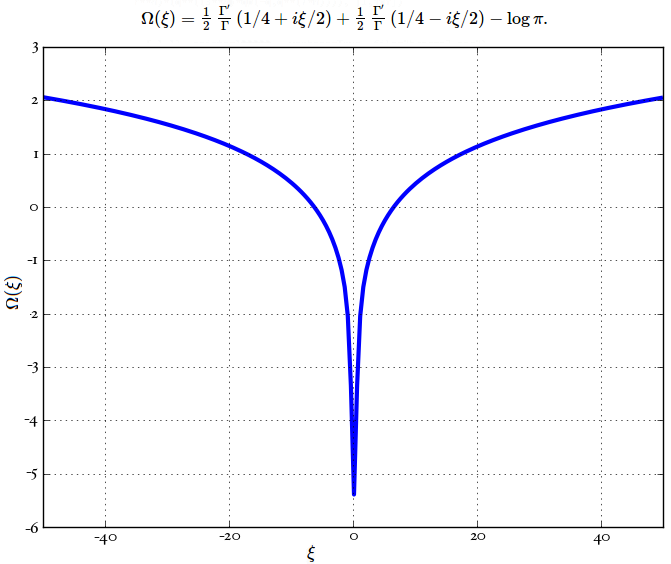
So, I’m thinking that the slow rise at right here:

might not be an artifact of numerical approximations, but an actual real thing: this function .
So: what’s the really neat way to write an ‘explicit formula’ relating prime powers and Riemann zeta zeros… which simplifies in some way iff the Riemann Hypothesis holds? And is there a way to modify Freeman Dyson’s claim here, that makes it correct while still maintaining a connection to quasicrystals?
If the Riemann Hypothesis is true, then the zeros of the zeta-function form a one-dimensional quasicrystal according to the definition. They constitute a distribution of point masses on a straight line, and their Fourier transform is likewise a distribution of point masses, one at each of the logarithms of ordinary prime numbers and prime-power numbers.




Re: Quasicrystals and the Riemann Hypothesis
The remark Dyson makes on definitions sounds rather akin to the decision by the International Union of Crystalographers to define “crystal” for the purposes of their art as “any solid having an essentially discrete diffraction diagram”.
Of course there is no need for mathematicians to adopt the same technical terminology as an International Union of Whichever (especially when “crystal” already means something very different in differential geometry), but whether you call them “quasicrystals” or “fourier-dual discretions” the notion is clearly interesting and probably worth giving some name.