A Categorical Semantics for Causal Structure
Posted by John Baez
guest post by Joseph Moeller and Dmitry Vagner
We begin the Applied Category Theory Seminar by discussing the paper A categorical semantics for causal structure by Aleks Kissinger and Sander Uijlen.
Compact closed categories have been used in categorical quantum mechanics to give a structure for talking about quantum processes. However, they prove insufficient to handle higher order processes, in other words, processes of processes. This paper offers a construction for a -autonomous extension of a given compact closed category which allows one to reason about higher order processes in a non-trivial way.
We would like to thank Brendan Fong, Nina Otter, Joseph Hirsh and Tobias Heindel as well as the other participants for the discussions and feedback.
Preliminaries
We begin with a discussion about the types of categories which we will be working with, and the diagrammatic language we use to reason about these categories.
Diagrammatics
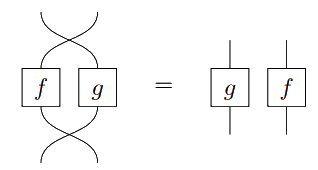
Recall the following diagrammatic language we use to reason about symmetric monoidal categories. Objects are represented by wires. Arrows can be graphically encoded as
Composition and depicted vertically and horizontally
satisfying the properties
and the interchange law
If is the unit object, and is an object, we call arrows states, effects, and numbers.
The identity morphism on an object is only displayed as a wire, and both and its identity morphism are not displayed.
Compact closed categories
A symmetric monoidal category is compact closed if each object has a dual object with arrows
and
depicted as and and obeying the zigzag identities:
Given a process in a compact closed category, we can construct a state by defining
This gives a correspondence which is called “process-state duality”.
An example
Let be the category in which objects are natural numbers, and morphisms are -matrices with composition given by the usual multiplication of matrices. This category is made symmetric monoidal with tensor defined by on objects and the Kronecker product of matrices on arrows, . For example
The unit with respect to this tensor is . States in this category are column vectors, effects are row vectors, and numbers are matrices, in other words, numbers. Composing a state with an effect , is the dot product. To define a compact closed structure on this category, let . Then and are given by the Kronecker delta.
A Categorical Framework for Causality
Encoding causality
The main construction in this paper requires what is called a precausal category. In a precausal category, we demand that every system has a discard effect, which is a process ![]() . This collection of effects must be compatible with :
. This collection of effects must be compatible with :
A process is called causal if discarding after having done is the same as just discarding .
If has discarding, we can produce a state for by spawning an and pair, then discarding the :
In the case of , the discard effect is given as row vector of ’s: . Composing a matrix with the discard effect sums the entries of each column. So if a matrix is a causal process, then its column vectors have entries that sum to . Thus causal processes in are stochastic maps.
A process is one-way signalling with if
and if
and non-signalling if both and .
The intuition here is that means cannot signal to ; the formal condition encodes the fact that had influenced the transformation from to , then it couldn’t have been discarded prior to it occurring.
Consider the following example: let be a cup of tea, and a glass of milk. Let the process of pouring half of into then mixing, to form milktea and half-glass of milk. Clearly this process would not be the same as if we start by discarding the milk. Our intuition is that the milk “signalled” to, or influenced, the tea, and hence intuitively we do not have .
A compact closed category is precausal if
1) Every system has a discard process ![]()
2) For every system , the dimension is invertible
3) has enough causal states
4) Second order causal processes factor
From the definition, we can begin to exclude certain causal situations from systems in precausal categories. In Theorem 3.12, we see that precausal categories do not admit ‘time-travel’.
Theorem If there are systems , , such that
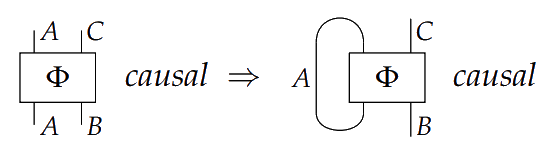
then .
In precausal categories, we have processes that we call first order causal. However, higher order processes collapse into first order processes, because precausal categories are compact closed. For example, letting ,
We can see this happens because of the condition . Weakening this condition of compact closed categories yields -autonomous categories. From a precausal category , we construct a category of higher order causal relations.
The category of higher order causal processes
Given a set of states for a system , define its dual by
Then we say a set of states is closed if , and flat if there are invertible scalars , such that ![]() ,
, ![]() .
.
Now we can define the category . Let the objects be pairs where is a closed and flat set of states of the system . A morphism is a morphism in such that if , then . This category is a symmetric monoidal category with . Further, it’s -autonomous, so higher order processes won’t necessarily collapse into first order.
A first order system in is one of the form ![]() . First order systems are closed under . In fact, admits a full faithful monoidal embedding into by assigning systems to their corresponding first order systems
. First order systems are closed under . In fact, admits a full faithful monoidal embedding into by assigning systems to their corresponding first order systems ![]() .
.
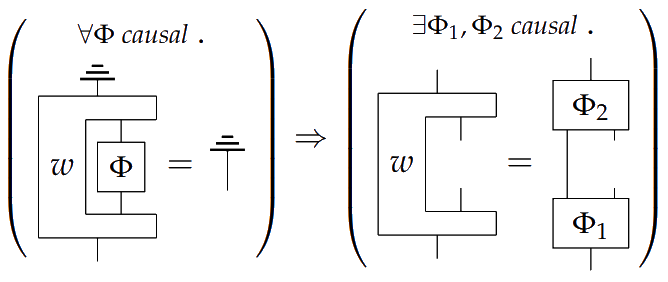
For an example of a higher order process in , consider a classical switch. Let
and let be the second order process
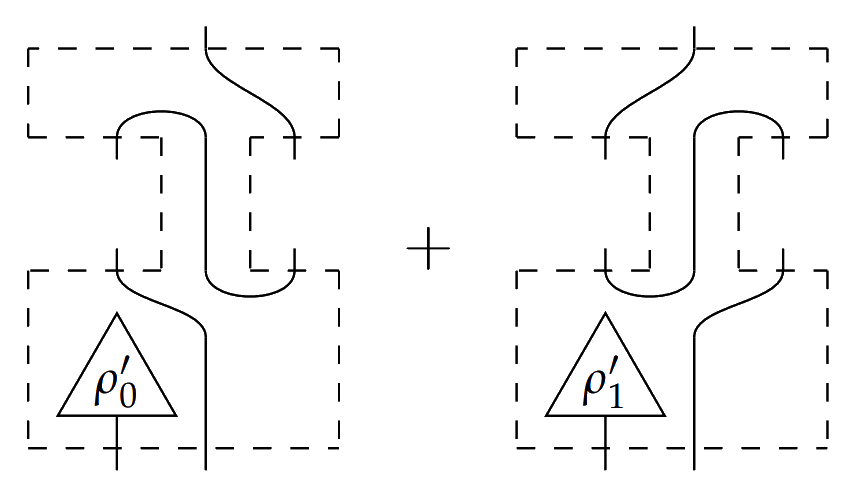
This process is of type , where the two middle inputs take types on the left and on the right. Since is if and otherwise, then plugging in either or to the bottom left input switches the order that the and processes are composed in the final output process. This second order process is causal because
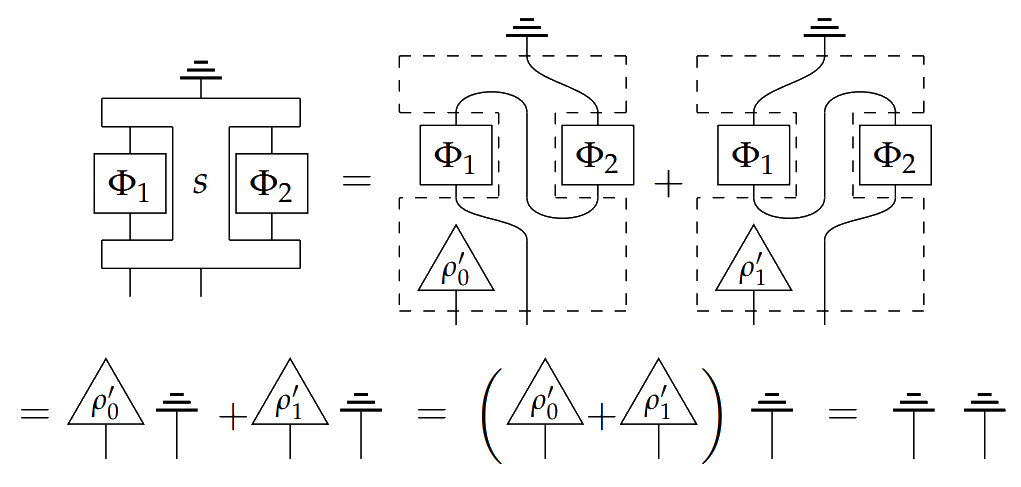
The authors go on to prove in Theorem 6.17 that a switch cannot be causally ordered, indicating that this process is genuinely second order.

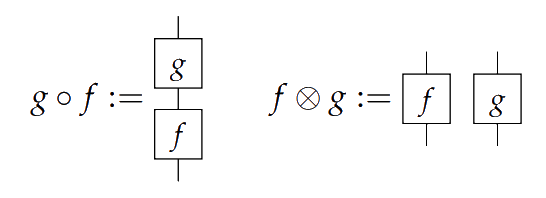

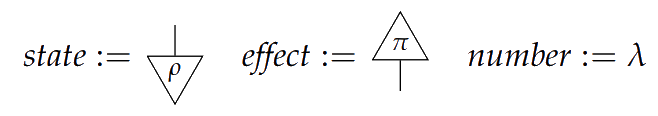
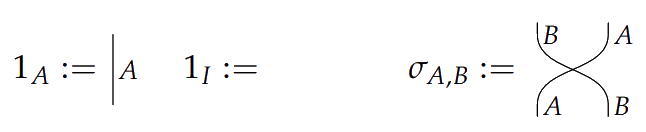
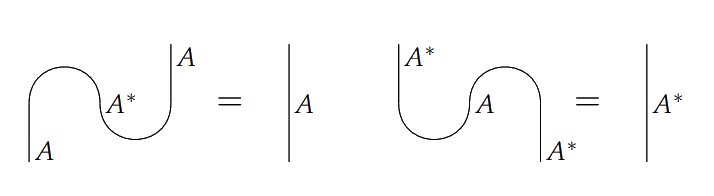
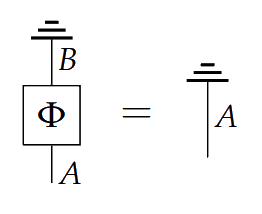
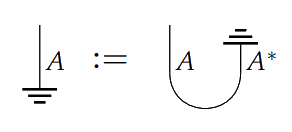
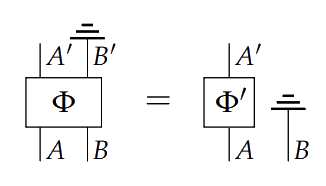
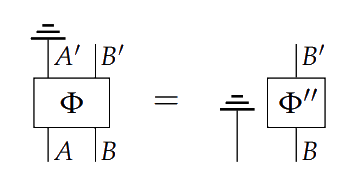
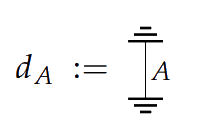
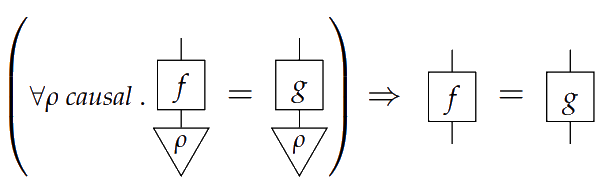
Re: A Categorical Semantics for Causal Structure
This was a very enjoyable read!
As you write, a process is causal if when we do it and then chuck the result, its the same as having chucked the input. I can see this as saying that the result of the process is really everything the process effects; getting rid of the result is the same as not having done the process at all. But I’m struggling to see how this relates to causality – probably because I don’t have much of an intuition for what a “causal process” is pre-theoretically. Would ya’ll be willing to elaborate on how this definition of a causal process deserves the name?