The n-Category Café

I’ll begin with a warning: this post is rambling and very long. Apparently I had a lot to say. For seven years I was obsessed with higher categorical structures. That obsession faded to an interest a while ago, and I spend most of my time now in other parts of mathematics. But still, higher category theory has played a large enough part in my life that questions such as ‘what do you think of the current state of higher category theory?’ inevitably have me asking myself larger questions such as ‘what do I think about category theory?’ and ‘what do I think about mathematics?’ Consider yourself warned!

What is category theory?

In my mind, ‘category theory’ has two meanings. The first is the obvious one. But sometimes I’ll be sitting in a category theory conference, listening to a category theorist talking about categories, and I’ll think to myself ‘that’s not category theory’. Then, I’m using ‘category theory’ in the second sense.

So what is this second meaning of ‘category theory’? I’ll explain with an example: Buffon’s noodle.

As you know, the Comte de Buffon’s château was floored with boards of equal width. The Comte had a needle that happened to be precisely as long as the floorboards were wide, which he enjoyed flinging to the floor at random. ‘What,’ he asked himself, ‘is the probability that my needle will land across a crack?’

There are many ways to solve the problem. I’m going to give you Barbier’s 1860 solution, which I learned from Klain and Rota’s book Introduction to Geometric Probability (1, 2, 3). This is one of the most beautiful pieces of mathematics I’ve learned in the last few years.

The first step is to generalize. Consider not just straight needles, but curved ones too.

The second step is to generalize again. Consider not just needles as long as the boards are wide — one unit, say — but curved needles of arbitrary length (‘noodles’).

The generalizations have to be steered in the right direction, though. Instead of asking ‘what is the probability that the needle crosses a crack?’, we ask ‘what is the expected number of times that the needle crosses a crack?’ This is a generalization, since a straight needle of unit length almost surely crosses at most one crack, and for an event that occurs at most once, the expected number of occurrences is simply the probability that it occurs at all.

So now we’ve got a much more general problem: for a curved needle of arbitrary length, what is the expected number of times that it crosses a crack?

To answer this, observe that if two curved needles are welded end to end, the expected number of crossings for the composite needle is the sum of the expected numbers of crossings for the two original needles. (The expectation of a sum of random variables is the sum of the expectations, even if the variables aren’t independent.) So by thinking of any given curved needle as the welding-together of a large number of small straight needles (and choosing a suitable definition of ‘curved’), we see that the expected number of crossings is proportional to the length.

So all that remains is to calculate the constant of proportionality. A circular needle of unit diameter always crosses the cracks exactly 2 times, and has length $\pi$, so the constant is $2/\pi$. Hence for Buffon’s original, unit-length, needle, the probability that it crosses a crack is $2/\pi$.

I claim that this is a superb piece of category theory in the second sense. Of course, this is absurd: there’s not a category in sight. But consider the following properties of Barbier’s argument, and perhaps you’ll see why I want to call it category theory:

• It’s highly conceptual, with almost no calculation. (Contrast other proofs.) You could easily explain it out loud to someone while walking in the park. The only point when you might be tempted to reach for pen and paper is the last step, calculating the constant of proportionality, but even that makes only a small demand on your powers of mental algebra.
• It solves the problem by moving to a higher level of generality — and getting the right level of generality, at that.
• The generalization wasn’t quite the most obvious one. Good generalization almost always begins by carefully preparing the ground. Here, this was the little observation that for events that occur at most once, expected value is the same as probability. A more obvious generalization would be to ask what the probability of crossing was for needles of arbitrary length.
• We see uniform behaviour across a class of objects (curved needles of arbitrary length). Under other circumstances this would be called functoriality or naturality.
• There is a piece of grit around which the pearl forms. You can never solve a specific problem by entirely general means: at some point, you have to make the link between the generalities and the specific situation that you started with. Here, the grit is the calculation of the constant $2/\pi$, got by thinking about a circular needle.

All these points are characteristic of (what I regard as) good category theory. Perhaps I should use a vague term such as ‘conceptual mathematics’ rather than ‘category theory’, if I want to apply it to non-categorical arguments such as this. I’m not too bothered about the choice of words; I only want to give an impression of a type of mathematics that I particularly value.

What isn’t category theory?

In a well-known piece of mathematical bitching, Miles Reid described the study of category theory for its own sake as

surely one of the most sterile of all intellectual pursuits

(Undergraduate Algebraic Geometry, p.116). I’ve become rather fond of that quotation, though not for the reason that Reid intended. ‘Sterile’ doesn’t only mean infertile or unproductive. It’s also what you want surgical instruments to be: clean, uncontaminated, disease-free. No one wants to be operated on with a dirty scalpel.

I’m going to clarify that point, because I can hear a sarcastic voice saying ‘oh, so you want to do category theory uncontaminated by real mathematics’. Category theory is at its best, I think, when it reflects what mathematicians actually do and shows how to do it better, when it functions as the mathematics of mathematics.

It doesn’t contradict this, though, that category theory has its own internal structure, concepts, and aesthetics. If a new categorical concept only seems natural from the point of view of one particular application, that’s dirtying the scalpel. (A categorical concept that only bears on one part of mathematics isn’t really a categorical concept at all.) If there’s a break in the conceptual trail — an ad hoc hypothesis or definition — that’s dirtying the scalpel too. I’ll give some examples in a moment.

These judgements are reversible: someone might come along later and show that the thing that looked so tailored to one particular application is, when viewed from the right angle, a completely natural concept. I’ll give an example of that, too. Category theory works because it’s clean, uncontaminated, sterile.

In other words, I’m about to explain just how fussy I am.

I’ll do this by listing some examples of what I call contamination. Since I don’t want to publicly criticize other people’s work, I’ll draw the examples either from my own work, or from parts of mathematics that seem old enough now that they’re common property.

A break in the conceptual trail  A good piece of category theory should be an unbroken conceptual trail that you can follow from beginning to end. There should be no conceptually dubious stretches. Barbier’s solution to the needle problem lives up to this gloriously. Here’s something that doesn’t.

For a few years now I’ve been very interested in notions of size. Central to this is the definition of the cardinality or Euler characteristic of a finite category. Now, on the one hand I’m almost certain that the definition is ‘right’: it satisfies all the criteria that I think it should, and it seems to produce satisfying results when used in several different areas of pure and applied mathematics (as demonstrated by ongoing joint work with Clemens Berger, Christina Cobbold, Mark Meckes, Catharina Stroppel and Simon Willerton.)

But on the other hand, the situation is not quite satisfactory. As a prelude to the definition of the Euler characteristic of a category, one has to define the notion of a ‘weighting’ on a category. Where does this definition come from? What is the conceptual justification? I don’t really know. My own motivation was from one particular application, on the combinatorics of finite sets. When I’m giving talks, the best I can do is to explain how I came to the notion of weighting (knowing full well that not everyone will be moved by this particular motivation) and draw some vague analogies. I can’t explain it by abstract considerations. It’s a conceptual gap.

A clever little thing  I’ve learned to be wary of anything in category theory that provokes the word clever. I don’t mean that I like my category theory stupid, of course. But if I ever catch myself thinking of something I’ve done as ‘my clever trick’ (and I have), then I know I’m in trouble. Each of those three words should ring alarm bells. It’s great for mathematics to be visionary, beautiful, etc., but if cleverness is the first quality that comes to mind then it suggests to me that something is insufficiently understood. When good conceptual mathematics has been done, everyone should feel that it belongs to them. It’s simply part of the general understanding, part of the landscape.

An unaesthetic notion  Here’s a demonstration of how fussy I am: I’m suspicious of the notion of subcategory. Actually, I feel like I’m compromising by calling that ‘fussy’, because for ages I assumed that anyone with a background in category theory would be equally suspicious. I assumed that was normal. But apparently it’s not.

So what’s wrong with subcategories? First there’s an almost sociological point: while subgroups are enormously important in group theory, and linear subspaces are enormously important in linear algebra and functional analysis, subcategories simply don’t feature so prominently in category theory. They’re a bit of a second-rate notion. Generally, instead of thinking about subcategories, we think about faithful functors, or functors reflecting isomorphism, etc. Sometimes you’ll start by contemplating some property of a subcategory, such as fullness or density, but then realize that the natural level of generality for the property isn’t ‘subcategory of a category’: it’s ‘functor’ — including, but not limited to, subcategory inclusions.

Then there’s a more mathematical point. Inclusion functors of subcategories are characterized by being faithful and injective on objects. When I say ‘injective on objects’, I mean injective up to equality. This is what is known in these parts as evil, and while I’m not totally on board with that usage, it should be enough to make one stop and think ‘am I really doing this right?’ If the condition were ‘full and faithful’ (as for full subcategories) or ‘faithful and reflects isomorphisms’, then at least these are wholesome conditions — though I’d still want to ask whether they can be shed. But ‘injective on objects’ is a pretty bizarre condition.

Here’s an example of how the notion of subcategory can lead to what I regard as poor-quality category theory. Again, the example is from my own work.

I spent a while developing a notion of ‘(strong) homotopy algebra’ for an operad — a non-algebraic notion, for those who know what I mean by that, in contrast to the previous, algebraic, notions such as Lada’s and Markl’s. (Now, at last, we’re edging into higher category theory.) I’ll explain it in the case of homotopy monoids, since that’s enough to get the point across.

It begins innocently enough. Let $\Delta$ be, as usual, the category of nonempty finite ordinals, and let $\mathbf{D}$ be the category of all finite ordinals. Thus, $\mathbf{D}$ has one more object than $\Delta$, and is a monoidal category under $+$. It’s easy enough to show that a simplicial set is the same thing as a (covariant) colax monoidal functor $$X: \mathbf{D} \to \mathbf{Set}.$$ Colax monoidal means that $X$ comes equipped with structure maps $$\xi_{m, n}: X(m + n) \to X(m) \times X(n), \qquad \xi_\cdot: X(0) \to 1$$ satisfying some coherence axioms. The same is true if you replace $\mathbf{Set}$ by any other category with products. In particular, it’s true for $\mathbf{Top}$.

Now, a monoid in $\mathbf{Top}$ — a topological monoid — is a colax monoidal functor $(X, \xi): \mathbf{D} \to \mathbf{Top}$ for which the maps $\xi_{m, n}$ and $\xi_\cdot$ are isomorphisms. So, we might define a homotopy monoid in $\mathbf{Top}$ to be a colax monoidal functor $(X, \xi): \mathbf{D} \to \mathbf{Top}$ for which the maps $\xi_{m, n}$ and $\xi_\cdot$ are homotopy equivalences. This turns out to be a good definition. In fact, it is equivalent to Segal’s much older notion of ‘special simplicial space’: $\xi_{m, n}$ and $\xi_\cdot$ are homotopy equivalences if and only if the famous ‘Segal maps’ of the corresponding simplicial set are homotopy equivalences. But the advantage is that (unlike with Segal maps) the definition of homotopy monoid is sensible even when the monoidal structure on the category of ‘spaces’ is not cartesian. This happens, for instance, if you want a notion of homotopy differential graded algebra; then your monoidal category of ‘spaces’ is chain complexes, with the tensor product.

Good as this may seem, danger is looming. For what is the general definition of ‘homotopy monoid’ implicit in the last paragraph? Well, we have some category $\mathcal{E}$, thought of as the category of spaces, we have a distinguished class of maps in $\mathcal{E}$ called ‘equivalences’, and we define a homotopy monoid in $\mathcal{E}$ as a colax monoidal functor $(X, \xi): \mathbf{D} \to \mathcal{E}$ for which the maps $\xi_{m, n}$ and $\xi_\cdot$ are equivalences. So the context for the definition is: a category $\mathcal{E}$ equipped with a subcategory, made up of all the objects but only the ‘equivalences’ between them. For everything to function correctly this subcategory should satisfy a couple of axioms, but the damage is already done. We’ve gone and dirtied the scalpel with a subcategory. I find this unnatural and unsatisfactory, and I never managed to re-do it to my satisfaction.

A suspended judgement  Sometimes a concept can be presented in a way that makes it look unnatural; but that doesn’t preclude the possibility that it really is natural.

For example, for a long time I couldn’t see where the notion of simplicial set came from. It was clear that simplicial sets played an important role in current mathematics, but what was the motivation for the concept? Sure, they’re presheaves on nonempty finite totally ordered sets, but why that particular combination of qualifiers, ‘nonempty’, ‘finite’ and ‘totally’? Why would you think of putting any kind of order on the vertices of a simplex? It was hard for me to believe that simplicial sets were an ad hoc notion; all the same, I couldn’t see where they came from abstractly.

But then I figured out a couple of things that convinced me that $\Delta$ was a canonical object of mathematics. I’ll tell this story very briefly. First, there is a canonical process that assigns to each nonsymmetric operad $P$ a monoidal category $\mathbf{D}_P$ and a category $\Delta_P$. When $P$ is the terminal operad, $\mathbf{D}_P = \mathbf{D}$ and $\Delta_P = \Delta$. (Specifically: $\mathbf{D}_P$ is the free monoidal category on a $P$-algebra, and contravariant functors from $\Delta_P$ to a finite product category $\mathcal{E}$ correspond to colax monoidal functors $\mathbf{D}_P \to \mathcal{E}$.) Second, there is a canonical process that assigns to each functor $U: \mathcal{B} \to \mathcal{A}$ satisfying certain conditions a (full, dense) subcategory $\Delta_U$ of $\mathcal{B}$. When $U$ is the forgetful functor from $\mathbf{Cat}$ to directed graphs, $\Delta_U = \Delta$. (Further details are here.)

So, while I really do care about keeping my categorical instruments scrupulously clean, I also recognize that something might initially look like a contaminant but not be one, after all. (The metaphor breaks down around here.) As with $\Delta$, the most interesting situation is when all the social signs point to something being a clean or canonical notion, but there is as yet no good abstract explanation of where it comes from. That’s when work needs to be done.

What is an $n$-category?

Now there’s a question I’d like to see answered.

Of course, lots of people have provided fragments of answers. In the second half of the 1990s there was a huge wave of proposals for how to define ‘$n$-category’. One striking thing about this was the astonishing diversity of the contributors, and their reasons for contributing. There’s John Power, trying to develop $n$-categories to advance computer science. There’s Todd Trimble, proposing a definition of $n$-category that fits snugly into algebraic topology. There’s Michael Makkai, wanting to use $\infty$-categories as a logical foundation for mathematics. There’s Carlos Simpson from algebraic geometry; there’s John Baez from mathematical physics.

What matters in the long term, though, is not your motivation but the mathematics you leave behind. And on this score, too, the diversity was striking. The conceptions of higher category embodied by these proposals were highly varied, some of them very different from the conceptions of higher category prevalent today. For example, Penon elegantly defined the monad for $\infty$-categories in a few lines, characterizing it by a universal property. In doing so, he carefully positioned the theory of $\infty$-categories in the landscape of all possible algebraic theories. There is nothing overtly homotopical or simplicial in this conception. Instead, we have a notion of $\infty$-category motivated in terms of universal algebra, with beautiful conceptual clarity.

During this period, new proposed definitions of $n$-category seemed to be popping up at a rate of one every few months, and some people started throwing up their hands and saying ‘Not another definition of $n$-category! That’s the last thing we need!’ My own feeling was the opposite. I wanted to encourage the diversity, and I put a lot of energy into trying to persuade people that they shouldn’t view the various definitions as competing, but rather as complementary ways of accessing this important concept. That’s part of the reason why I wrote a survey of the proposed definitions that existed at the time. Gathering together many different ways of looking at one hard-to-reach concept — $n$-category — can help us to discern the common factors. It’s only by coming at a concept from several different angles that we can gain the rounded understanding that is part of good category theory. We still don’t have a rounded understanding of what an $n$-category is.

I need to say something about algebraic and non-algebraic notions of $n$-category, because I’ll be using these words later. Here and everywhere else, $n \in \mathbb{N} \cup \{\infty\}$ and ‘$n$-category’ means ‘weak $n$-category’.

Roughly speaking, proposed definitions of $n$-category fall into two groups. In the first, the algebraic, an $n$-category is defined as an $n$-globular set ($n$-graph) equipped with extra structure. Other ways of saying more or less the same thing are that the category of $n$-categories and strict $n$-functors is monadic over $n$-globular sets, or that $n$-categories are the models in $\mathbf{Set}$ for a finite limit theory. These three formulations aren’t precisely equivalent, and algebraic is only a semi-technical word, but I’ve never met a proposed definition of $n$-category for which I’ve had trouble deciding whether it’s algebraic or not.

The second group is everything else — the non-algebraic notions of $n$-category. Almost all such definitions are of the form ‘an $n$-category is a presheaf on such-and-such a category satisfying such-and-such conditions’.

There’s a general principle telling us that any algebraic notion of $n$-category can also be understood as a non-algebraic notion. (See the last two pages of these slides.) So the class of algebraic notions embeds into the class of non-algebraic notions. This, then, is the mathematical ‘non’: ‘non’ as in ‘non-commutative ring’, really meaning ‘not necessarily’. Just as commutative rings can be regarded as very special types of ring, the algebraic definitions can be regarded as very special notions of $n$-category.

Progress in mathematics sometimes entails throwing away everything we thought we knew. Often, though, bodies of mathematics fall into obscurity through the forces of fashion or historical accident, not as a result of rational judgement. Mathematics has a constant tendency to fragment; mathematicians have a constant tendency to march off, with great speed and enthusiasm, in opposite directions to each other. One of the justifications for the existence of category theory is that it counteracts this fragmentation. Part of a category theorist’s job is to be a curator of unfashionable causes.

What is the Homotopy Hypothesis?

There’s an old joke:

Q.  How do you prove the Homotopy Hypothesis?

A.  Define an $\infty$-groupoid to be a Kan complex; define a space to be a Kan complex; done!

I’m going to explain what the Homotopy Hypothesis is (or how I think of it), and what would qualify as a satisfactory solution. Among other things, I’ll take that joke solution seriously and try to explain what, in fact, is wrong with it.

The Homotopy Hypothesis says, informally, that

$\infty$-groupoids are the same as spaces.

A more refined version is: for each $n \in \mathbb{N} \cup \{\infty\}$,

$n$-groupoids are the same as $n$-types.

The first version is the case $n = \infty$ of the second, since ‘$\infty$-type’ is meant to mean the same as ‘space’.

All the terms in the Homotopy Hypothesis — ‘$\infty$-groupoid’, ‘same as’, and ‘space’ — are up for negotiation. Various interpretations of them have been suggested. Evidently, we can’t say that we fully understand the Homotopy Hypothesis until we fully understand the terms in its statement. This would mean, in particular, fully understanding what an $\infty$-groupoid is. Of course, this is closely related to the challenge of understanding what an $\infty$-category is, discussed in the previous section.

My mental picture of the Homotopy Hypothesis looks something like this:

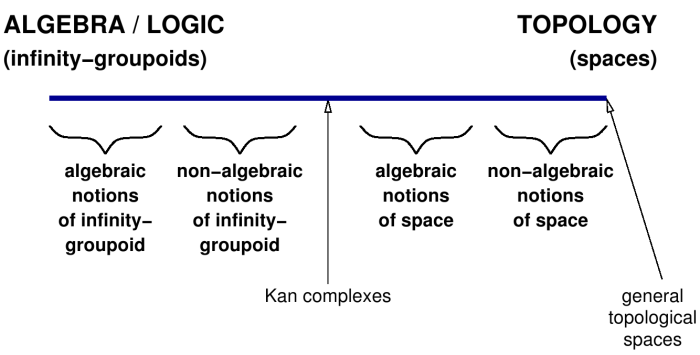
I’ve already explained the contrast between algebraic and non-algebraic notions of $\infty$-groupoid. Actually, I explained it for $n$-categories, but the issues are the same. For example, in Grothendieck’s Pursuing Stacks — one of the first written formulations of the Homotopy Hypothesis — the concept of $\infty$-groupoid is an algebraic one; Grothendieck specifies that they are to be a finite limit theory.

Now I need to say something about notions of space.

People can be a bit sniffy about general topological spaces. Personally, I think it’s remarkable that a single definition encompasses so many very different types of ‘space’. As some us were discussing recently at Math Overflow, topological spaces can very crudely be divided into three classes:

1. the spaces that algebraic topologists think most about (CW-complexes, roughly)
2. the ‘spectra’ (in various senses, but excluding that of homotopy theory)
3. the infinite-dimensional spaces that arise in functional analysis (e.g. Banach spaces).

In algebraic topology there has been detailed study of the process of taking a space in Class 1 and moving it leftwards — away from topology and towards algebra — by equipping it with a combinatorial structure such as a triangulation or a cell decomposition. The contrast, then, is between purely topological notions of space (such as the general notion of topological space, or topological spaces satisfying some convenient condition) and more combinatorial or algebraic notions of space (such as simplicial set). This is what I mean by ‘algebraic’ and ‘non-algebraic’ notions of space. I’m using these terms pretty vaguely, and I don’t claim that there’s the kind of definite distinction that there is between algebraic and non-algebraic notions of $\infty$-groupoid. All the same, I hope it’s not so vague that you can’t see what I mean.

More vaguely still, the right-hand end of the line represents topological spaces as conceived by someone who is not thinking at all algebraically or combinatorially. It’s pure continuity; it’s the image of a sphere that forms in the mind of a child; it’s the feeling of nearness that we get as we move on a paint chart from ‘tropical aqua’ to ‘marine blue’ to ‘ocean azure’. The middle region of the line is where simplicial structures live: simplicial notions of space and simplicial notions of $\infty$-groupoid. For example, the algebraic Kan complexes that Thomas told us about recently are located in the right-hand part of the region labelled ‘algebraic notions of infinity-groupoid’. The left-hand end of the line represents $\infty$-groupoids as conceived by someone who is not thinking at all topologically. An $\infty$-groupoid is a globular set equipped with some operations satisfying some equations.

To make the Homotopy Hypothesis stand a chance of being true we need to restrict the word ‘space’ to mean something like ‘space of Class 1’, since these are the spaces that can be probed effectively by the real interval. I’ll use the word ‘space’ in this restricted way from now on.

A full-strength statement of the Homotopy Hypothesis will say, then, that

$\infty$-groupoids in a fully algebraic sense

are the same as

spaces in a fully non-algebraic sense

and similarly with ‘$n$-groupoids’ in place of ‘$\infty$-groupoids’ and ‘$n$-types’ in place of ‘spaces’. In other words, it matches up the leftmost and rightmost ends of the line; it shows that the whole thing can be collapsed to a point. Diluted statements of the Homotopy Hypothesis might use a non-algebraic notion of $\infty$-groupoid or an algebraic notion of space (or, indeed, a diluted notion of sameness). The extreme of dilution is the joke solution.

So what’s wrong with the joke solution? It’s a question worth taking seriously. In fact, someone asked me exactly this question, differently phrased, a couple of years ago at a conference in Split. Why not define an $\infty$-groupoid to be a Kan complex? Why not define a space to be a Kan complex?

My answer calls on the general points I made about category theory earlier. Good categorical definitions are not tailored to any particular application. Their strength is in their flexibility, their adaptability to multiple parts of mathematics, some as yet unknown. You could define an $\infty$-groupoid to be a Kan complex, but that would be to emphasize the topological and simplicial aspects of $\infty$-groupoids as the expense of other aspects. For example, if you want to think of $\infty$-groupoids as globular sets with structure then this definition is immediately un-ideal; even taking the underlying globular set of a Kan-complex-as-$\infty$-groupoid is a somewhat worrisome process. Similarly, you could define a space to be a Kan complex, but that would be to emphasize the simplicial aspects of topology above all others. We don’t always want to think of a space as a simplicial set. Kan complexes, and simplicial structures in general, do seem to be important; but not everything in life is naturally simplicial.

What would I like to see?

I spent a long time above explaining my taste in category theory. Here I’ll add a few things more particularly about higher category theory, and finish with some more personal comments.

The ultimate excitement would be a conceptually satisfying theory of categorification. This would include a conceptually satisfying theory of higher categories. At the time when I stopped focussing on higher category theory, I had a feeling that we — humanity at large — were missing at least one big idea about higher categories. I have that feeling still.

Really this encompasses everything else, but I’ll describe some aspects that I’d especially like to see.

One would be learning how to stop handwaving over the word ‘the’. This issue will be familiar to most people who’ve had much contact with category theory. We say ‘the product of two sets’, for example, and we reason as if it really were a definite set rather than an isomorphism class of sets, and we justify this by the fact that products are unique up to canonical isomorphism. Nevertheless, the act of choosing a product for each pair of sets is distasteful and sometimes inconvenient. The issue is both magnified and brought into focus in higher category theory. We all feel that we know what we mean by this ‘generalized the’, but handwaving is what it is. Here’s Rota again:

The simplest, and most remarkable, application of the definition of species is the rigorous combinatorial rendering of functional composition, which was formerly dealt with by handwaving — always a bad sign.

This is from Rota’s foreword to the book of Bergeron, Labelle and Leroux, Combinatorial Species and Tree-Like Structures. It’s no coincidence that the remedy for handwaving that Rota was talking about was also a piece of category theory (Joyal’s beautiful notion of species). Category theory has a long history of curing handwaving, from ‘natural transformation’ onwards.

I’d also like to see advances in our understanding of the nebulous concept of ‘sameness’. This is in the province of $\infty$-groupoid theory, and is related to the previous paragraph: any two products of a pair of objects are ‘the same’, for instance. I think the most precise expression of the idea that we’ve seen so far has been in work connecting higher category theory with type theory, such as the work of Awodey, van den Berg, Garner, Lumsdaine and Warren. I know regrettably little about this, and my outsider’s impression is that even those carrying out this work consider the story to be just beginning. (I hope they’ll correct me if I’m wrong.) But it would be great to see this go further and deeper.

I’ll finish with a couple of more personal things. For the seven years that I was working intensively on the subject, almost everything in higher category theory fascinated me. Now that the subject’s grown and I’ve moved on, it’s inevitable that that’s no longer the case. Some parts sing to me; some just don’t.

During that time I had a lot of energy for what you might call ‘refinement’. At the time (and maybe still) many papers on higher categorical structures contained excellent ideas, but obscured by what seemed to be hair-raising complications. I don’t mean this as a slur: original work often is messy. I put a lot into trying to refine this raw material, simplify, reshape, bring out the categorical essence. It’s a wholly worthwhile pursuit, I think, but it’s also very time-consuming. Nowadays I’m directing my energy elsewhere, so if a piece of work in higher category theory looks like a mess then I’ll probably just ignore it and think about something more appealing, rather than going in to try to clean things up as I would have done previously.

I don’t think I’m very mathematically goal-oriented. My view is that human beings know only epsilon about mathematics, and will still know only epsilon about mathematics on the day the universe dies. There’s an infinite amount of mathematics out there, and I’m more interested in getting things done right than getting them done fast. We’ll never get to the end anyway. Of course, ‘right’ is highly subjective, and probably just means ‘in a way that I find satisfying’. But this is roughly the reason why I’ve never had a problem with the idea of spending a long time making definitions without ever proving a theorem. I value the art of laying good foundations, and on most days I’m not in a hurry to go building on them before they’re ready. Other people are different; it’s a personal thing. And I now find myself thinking of Douglas Adams in The Hitchhiker’s Guide to the Galaxy:

Orbiting this at a distance of roughly ninety-eight million miles is an utterly insignificant little blue-green planet whose ape-descended life forms are so amazingly primitive that they still think digital watches are a pretty neat idea.