Each $n$-simplex of an quasi-category exhibits some composite of the $n$ morphisms which make up its spine. We will argue that these simplices can be regarded as “unbiased associahedra” in the sense that they witness the “commutativity” of their boundaries, which are $n-1$-simplices of the same form. In fact, one may choose all but one of these $n-1$-simplices to be any witnesses that you want, subject to some obvious constraints. We will describe in detail the combinatorial analogies between these constraints and Stasheff’s associahedra in what follows, at least in low ($n \leq 6$) dimensions.

Before turning to these concrete details, we should acknowledge a more conceptual explanation for the experts in this field, due to Jacob Lurie, for the phenomena we’ll describe below. The theory of quasi-categories is equivalent to the theory of simplicial (or topological) categories. One feature of this equivalence is that the mapping spaces in any quasi-category (however one chooses to extract them) are homotopy equivalent to mapping spaces in a simplicial category, where there is a strictly associative multiplication. Transporting this structure along the homotopy equivalences will give an $A_{\infty}$ structure on the mapping spaces in the original quasi-category. By definition, $A_{\infty}$-spaces are algebras for the non-$\Sigma$ operad $\{ K_n \}$ with objects given by Stasheff’s associahedra, accounting for their appearance in what follows.

We begin by explaining the construction of the homotopy category of an quasi-category, emphasizing the role played by the 2- and 3-simplices. The reader who already knows this story can comfortably skip to the next section, after making note of our convention for labeling 3-simplices. In the second section, we describe the low-dimensional higher associativity data that is present in any quasi-category, beginning with $n=4$ and then moving on to $n=5$ and $n=6$. A LaTeXed version of this post with even more details can be found here.

Preliminaries, or how is an $(\infty,1)$-category “category-like”?

We’ll use standard notation for simplicial sets, which agrees with Lurie’s Higher Topos Theory or his article “What is an $\infty$-category?” from the Notices of the AMS, although we prefer the name quasi-category for his $\infty$-category. In particular, we write $\Delta^n$ for the simplicial set ${\mathbf{\Delta}}^{\text{op}} \rightarrow \mathbf{Set}$ represented by the object $[n] = \{0,1,\ldots,n\}$ of ${\mathbf{\Delta}}$. If $S : {\mathbf{\Delta}}^{\text{op}} \rightarrow \mathbf{Set}$ is a generic simplicial set, $S_n$ is the set of its $n$-simplices. We have face maps $d_i : S_n \rightarrow S_{n-1}$ and degeneracy maps $s_i : S_n \rightarrow S_{n+1}$ for $0 \leq i \leq n$. A horn $\Lambda^n_i$ is a simplicial subset of $\Delta^n$ (or also of its boundary $\partial \Delta^n$). It is generated by $n$ $n-1$-simplices which satisfy the relations typical of the collection of all faces but the $i$th of any $n$-simplex. We are more often interested in relative horns, i.e., maps $\Lambda^n_i \rightarrow S$. Concretely, these are specified by elements $\sigma_0, \ldots, \hat{\sigma_i}, \ldots \sigma_n \in S_{n-1}$ (the images of the generating $n-1$-simplices mentioned previously) satisfying the relations

An quasi-category is a simplicial set $S$ such that every inner horn can be filled, which means that for every collection of $n-1$-simplices as above with $0 \lt i \lt n$, there exists $\sigma_i \in S_{n-1}$ and $\sigma \in S_n$ such that the faces of $\sigma$ are precisely the $\sigma_j$.

Fix an quasi-category $S$. It is category-like in the following sense. We regard the vertices aka points aka 0-simplices as objects and edges aka arrows aka maps aka 1-simplices $f \in S_1$ as morphisms from $d_1f$ to $d_0f$; we write $d_1f \stackrel{f}{\rightarrow} d_0f$. For any $x \in S_0$, $s_0x \in S_1$ is a morphism from $x$ to $x$, which we regard as the identity at $x$ and depict with an equals sign.

We will depict 2-simplices like this

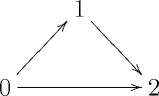
The vertices will always be in the same position, so we typically omit the numbers. The $i$th edge is the edge opposite vertex $i$. We say morphisms $f$ and $f'$ with the same endpoints are homotopic if there exists a 2-simplex with boundary

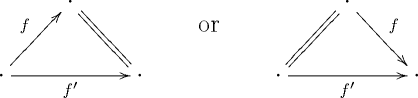
or with $f$ and $f'$ switched. In an quasi-category, this defines an equivalence relation and furthermore any one of these conditions implies all of the others.

Importantly, we have a weak composition law defined as follows. Morphisms $f$ and $g$ are composable when the codomain $d_0f$ equals the domain $d_1g$, i.e., exactly when

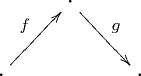
determines a horn $\Lambda^2_1 \rightarrow S$ (in words, a 2,1-horn in $S$). Any 2-simplex $\sigma \in S_2$ that fills this horn exhibits the edge $d_1\sigma$ as a composite of $f$ and $g$. As $S$ is an quasi-category, some such $\sigma$ always exists. In an quasi-category, any two such composites are homotopic, and furthermore if we replace $f$ or $g$ by homotopic maps, the composites are still homotopic.

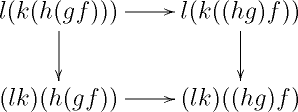
All of the unproven claims above follow easily by filling 3,1- or 3,2-horns in $S$ to obtain a 3-simplex. By constructing the horn appropriately, the “missing face” that is given by its filler will be the desired 2-simplex (exhibiting, e.g., that some arrow is a composite of two other arrows, or that some pair of arrows are homotopic). Let’s agree to draw 3-simplices like this

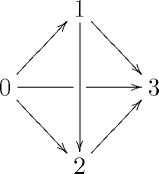
The vertices will always be in the same position, so we typically omit the numbers. Using the conventional numbering for simplices, the 3rd face is the left face, the 2nd face is the back face, the 1st face is the bottom face, and the 0th face is the right face.

We can now prove that composition is associative up to homotopy. Suppose we have three composable morphisms $f$, $g$, and $h$ and let us choose composites $g f$ and $h g$, as well as 2-simplices exhibiting these chosen composites. We can either choose a composite $h(g f)$ and show that it is a composite of $f$ and $h g$ or choose a composite $(h g)f$ and show that it is a composite of $g f$ and $h$. The former strategy amounts to filling the 3,2-horn depicted by

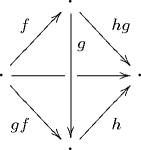
with the back arrow equal to the chosen morphism $h(g f)$. Filling this horn fills in the back face, which exhibits $h(g f)$ as a composite of $f$ and $h g$. The latter strategy amounts to filling the 3,1-horn also depicted by (2) but with the back arrow equal to $(h g)f$. It follows that $h(g f)$ and $(h g)f$ are homotopic, as they are both composites of the same morphisms.

We have proven that the simplicial set $S$ is category-like: given $S$ we can obtain an actual category with objects the 0-simplices and morphisms homotopy classes of 1-simplices. The facts stated above define composition on homotopy classes and prove that it is associative and unital. This category is called the homotopy category of $S$ and is depicted in the literature by $\tau_1S$ (in the unpublished work of André Joyal) or h$S$ (by Jacob Lurie). However, a lot of data is lost when we forget about $S$ and work instead with its homotopy category, which is why quasi-categories are objects of interest in their own right.

Higher associativity data

With these preliminaries aside, we are now finally able to address the following question: what sort of higher associativity data is present in any quasi-category? First, a definition from the theory of simplicial sets: the spine of an $n$-simplex $\sigma \in S_n$ consists of the edges $0 \rightarrow 1$, $1 \rightarrow 2$, $\ldots$ , $n-1 \rightarrow n$ between the successive vertices of $\sigma$. In the language of the previous section, the spine of $\sigma$ is the maximal list of composable edges of $\sigma$. When $n\gt 2$, a $n,i$-horn in $S$ has the same edges as any of its fillers, so we may speak of the spine of a horn as well. For example, in (2), the spine is $f$, $g$, $h$.

Given a sequence $f$, $g$, $h$ of three composable morphisms, any 3-simplex with spine $f$, $g$, $h$ gives a piece of associativity data associated to that sequence. The faces of any such simplex exhibit composites $g f$ and $h g$ as well an an arrow $d_1f \rightarrow d_0h$ that is simultaneously exhibited as a composite of $f$ with $h g$ and $g f$ with $h$. The work of the previous section shows that such simplices exist in any quasi-category. This sort of associativity data is more natural than that exhibited, e.g., by a 3-simplex

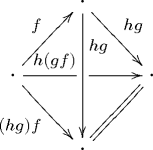
that fills the 3,1-horn with faces constructed from the faces of (2). This is because the former is unbiased, whereas the latter emphasizes the chosen composite $h g$ and neglects to choose a composite of $f$ and $g$.

With this in mind, the next level of associativity data should consist of 4-simplices with spine $f$, $g$, $h$, $k$, where this is again a sequence of composable morphisms. We will show firstly that such simplices can be constructed in any quasi-category and secondly that the faces of any such simplex can be understood as some sort of “unbiased associativity pentagon.” We will then explain how the observations made for 4-simplices extend to 5- and 6-simplices, which we explicitly relate to the (rather more complicated) associahedra $K_5$ and $K_6$, after which point we become tired of computing associahedra and stop.

4-dimensional associativity

First, we will construct a 4-simplex that should be thought of as a piece of associativity data for the sequence of composable morphisms $f$, $g$, $h$, $k$. We will construct this simplex by filling a 4,2-horn. It is also possible to construct such a 4-simplex by filling a 4,1- or 4,3-horn but such constructions feel somewhat less natural. Details for these other cases can be found here.

Any 4-simplex $\sigma$ has five faces $\sigma_0, \ldots, \sigma_4$, which are themselves 3-simplices. We will construct our 4-simplex by filling the 4,2-horn given by the 3-simplices depicted below, which are themselves constructed by filling 3-dimensional horns:

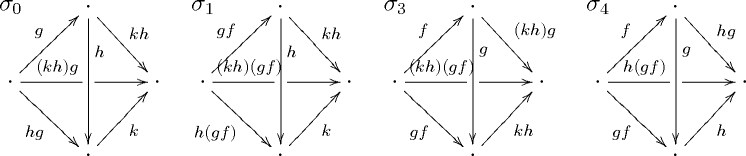
The labels for the arrows are meant to indicate how these composites are chosen. We begin by choosing 2-simplices exhibiting composites $g f$, $h g$, and $k h$ of the 3 composable pairs contained in our list of morphisms. Next, we choose simplices exhibiting the composites $h(g f)$ and $(k h)g$ that will form the 3rd face of $\sigma_1$ and $0$th face of $\sigma_3$, respectively. With the data previously chosen, we can form a 3,1-horn, which we fill to obtain $\sigma_0$ and a 3,2-horn, which we fill to obtain $\sigma_4$. Finally, we choose a 2-simplex exhibiting a composite $(k h)(g f)$ of $k h$ and $g f$. This allows us to construct a 3,1-horn, which we fill to obtain $\sigma_1$ and a 3,2-horn, which we fill to obtain $\sigma_3$.

We must show that these 3-simplices fit together to form a 4,2-horn in $S$. The conditions that we must check are

Each of these six conditions asks that we have agreed on the 2-simplex that we have chosen to exhibit the indicated composite. E.g., the first condition asks that we have chosen a 2-simplex exhibiting a particular composite of $f$ and $g$. Hence, the above procedure gives rise to a 4,2-horn, which we can fill in $S$ to obtain the desired 4-simplex $\sigma$.

How can we understand this 4-simplex? First, note that its 5th face is

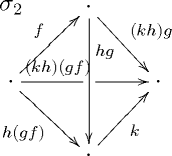
The faces of $\sigma_2$ are exactly the things we haven’t chosen already: 2-simplices exhibiting $k(h g)$ as a composite of $h g$ and $k$, $(h g)f$ as a composite of $f$ and $h g$, and $(k h)(g f)$ as a composite of both $f$ and $(k h)g$ and $h(g f)$ and $k$.

Importantly, the five faces of $\sigma$ can be associated with the edges of the associativity pentagon. Using common notation for the latter (such as in the context of a monoidal category), the associations are as follows:

These associations are easily recognized from the spines of each $\sigma_i$. These five simplices form a simplicial sphere in $S$, i.e., a map $\partial \Delta^4 \rightarrow S$, and $\sigma$ fills this sphere. (An $n$-dimensional simplicial sphere in $S$ is specified by $n+1$ $n-1$-simplices $\sigma_0,\ldots, \sigma_n$ satisfying the relations of (1), except dropping the requirement that $j,k \neq i$.) In common parlance, a simplicial sphere commutes exactly when it can be filled. So $\sigma$ witnesses the fact that the sphere formed by the 3-dimensional associativity data $\sigma_0$, $\sigma_1$, $\sigma_2$, $\sigma_3$, $\sigma_4$ commutes. In contrast to the situation of the associativity pentagon, this commutativity is unbiased; we don’t have a natural way of composing 3 simplices so we don’t attempt to combine them in any particular order.

5-dimensional associativity

Now we move up a level to consider 5-simplices that can be thought of as a piece of associativity data for the sequence of composable morphisms $f$, $g$, $h$, $k$, $l$. Any 5-simplex has six faces, which we identify by their spines. Given a 5-simplex $\sigma$ with spine $f$, $g$, $h$, $k$, $l$, its faces have the spines indicated:

As before it is possible to make a sequence of choices in such a way as to construct a 5,1-, 5,2-, 5,3-, or 5,4-horn whose filler $\sigma$ is such an associativity 5-simplex. Rather than describe the details of such a construction, we switch perspectives somewhat and consider together all of the relations satisfied by the six faces that form the simplicial sphere filled by $\sigma$. They are listed in the following table:

These relations ask that certain faces of the 4-simplices $\sigma_i$ are equal, i.e., that we choose certain 3-simplices consistently when constructing the $\sigma_i$. We’ll identify these chosen 3-simplices with their spines for simplicity. The requirement that two 3-simplices are equal implies that their faces are the same, so we don’t care to specify what these 2-simplices are anymore.

The top three rows of relations correspond, respectively, to the 3-simplices with spines

These correspond to the nine edges of the associahedron $K_5$

that are shared by two pentagonal faces in the same manner of the correspondence given in the previous section: namely, the 3-simplex with spine $x,y,z$ is associated to $\alpha_{x,y,z}$. This should be compared with (4).

The relations in the fourth row correspond, respectively, to the 3-simplices $f,g,h$; $g,h,k$; and $h,k,l$. We will say more about these relations in a moment. The final row of relations correspond, respectively, to the 3-simplices with spines $h g f, k, l$; $f, k h g, l$; $f,g, l k h$. The morphism $h g f$ should be the back edge of the 3-simplex $f,g,h$ serving as a common composite for $f$ with $h g$ and $g f$ with $h$, and similarly of course for the other triples. These last two rows of relations correspond to the edges of the associahedron $K_5$ that surround the three “naturality squares” in the following manner. For example, the relation $d_4\sigma_5 = d_4 \sigma_4$ corresponds to the top and bottom arrows of the “naturality square” below; note that these arrows arise from the same natural transformation $\alpha_{f,g,h}$.

The relation $d_1\sigma_2 = d_1\sigma_1$ corresponds to the left and right arrows of this square, which arise from the natural transformation $\alpha_{h g f, k, l}$.

The reason these faces of the associahedron are squares and not some other shape has to do with the fact that the information they contain is somehow the product of two $K_3$, which are intervals geometrically. In the example above, one $K_3$ (or, extending our analogy downward, one 3-simplex) contains the data associated with the triple $f,g,h$ while the other contains the data associated with the triple $h g f, k, l$. The product of these two intervals is a square. When we describe the associahedron $K_6$ in the next section, we will see that it is productive to think of some of its faces as (non-trivial) products in a similar manner.

In conclusion, the 5-simplex $\sigma$ can be viewed as data witnessing the commutativity of an unbiased 5-dimensional associahedron whose faces correspond to the lower-dimensional data described above.

6-dimensional associativity and beyond

We extend this analogy one dimension further in part to clarify how the ”naturality squares” of $K_5$ generalize to higher dimensions. The associahedron $K_6$ is the 4-dimensional polytope whose vertices correspond to each way of multiplying (non-associatively) an ordered list of six elements. Alternatively, each vertex corresponds to a planar rooted binary tree with six leaves. $K_6$ has 14 faces, which are themselves polyhedra. Seven of these take the form of the associahedron $K_5$ while the other seven are pentagonal prisms (geometrically equal to $K_4 \times K_3$).

As was the case for lower dimensions, one can construct a 6-simplex with spine $f, g, h, k, l, m$ by filling a 6,$i$-horn for some $0 \lt i \lt 6$, where the faces of the horn are also constructed by filling horns. As usual, these faces must satisfy the relations (1). We again omit the details of this construction and instead describe the combinatorics of such 6-simplices.

A 6-simplex $\sigma$ with spine $f, g, h, k, l, m$ will have seven faces corresponding to the seven associahedral faces of $K_6$. The faces $\sigma_0, \ldots, \sigma_6$ satisfy 21 relations, which describe how these 5-simplices are glued together to form the boundary of $\sigma$. Each associahedral face of $K_6$ is glued along its pentagonal faces to each other face either directly or via a connecting prism, and these gluings correspond bijectively to the 21 relations mentioned above. Additionally, the three squares of an associahedral face are glued to square faces of three separate pentagonal prisms, and some of the pentagonal prisms are glued to each other directly along the remaining square faces. We understand this “lower level gluing” to correspond to the choices that had to be made prior to constructing the 4-simplices that will serve as faces of the $\sigma_i$. This should be compared with the observation in the previous section that we had to choose a morphism $h g f$, which should be the back edge of the 3-simplex $f, g, h$ before constructing the 3-simplex $h g f, k, l$.

The conclusion is the same as we have asserted previously: a 6-simplex $\sigma$ can be viewed as data witnessing the commutativity of the unbiased 6-dimensional associahedron whose faces correspond to the lower-dimensional data described above.