This Week’s Finds in Mathematical Physics (Week 276)
Posted by John Baez
In week276 of This Week’s Finds, hear the shocking news about this star:

Read about the Local Bubble, the Loop I Bubble, the cloudlets from Sco-Gen, and the “local fluff”. Come visit the Lab! And learn how Paul-André Mélliès and Nicolas Tabareau have taken some classic results of Lawvere on algebraic theories and generalized them to other kinds of theories, like PROPs.
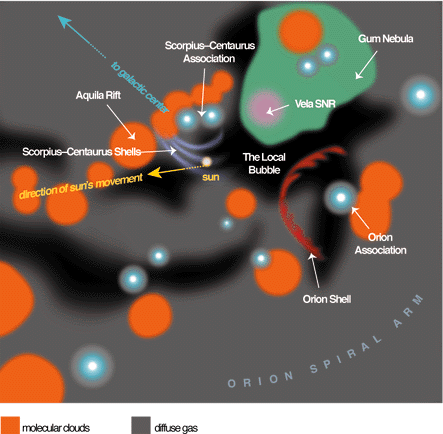
This picture, prepared by Linda Huff and Priscilla Frische, gives a more detailed view of our Solar’s system’s vicinity in the Milky Way:
It’s complicated! I don’t understand most of it.




Re: This Week’s Finds in Mathematical Physics (Week 276)
John says that:
I always had the impression that the free bialgebra on a vector space does always exist! After all, the free monoid on a vector space certainly exists, and that has a canonical bialgebra structure, so there’s an obvious functor from a category of vector spaces to its category of internal bialgebras and bialgebra homomorphisms.
Is the idea that there’s no adjoint to the forgetful functor from the category of internal bialgebras to the underlying category of vector spaces? I suppose the thing that would go wrong is that the canonical map from the free monoid on equipped with the canonical comultiplication, to an arbitrary bialgebra on , fails to be a bialgebra homomorphism in general. Difficult to prove this without a good way to characterize bialgebras, though.