A Graphical Calculus for Proarrow Equipments
Posted by John Baez
guest post by David Myers
Proarrow equipments (which also go by the names “fibrant double categories” and “framed bicategories”) are wonderful and fundamental category-like objects. If categories are the abstract algebras of functions, then equipments are the abstract algebras of functions and relations. They are a fantastic setting to do formal category theory, which you can learn about in Mike’s post about them on this blog!
For my undergraduate thesis, I came up with a graphical calculus for working with equipments. I wasn’t the first to come up with it (if you’re familiar with both string diagrams and equipments, it’s basically the only sort of thing that you’d try), but I did prove it sound using a proof similar to Joyal and Street’s proof of the soundness of the graphical calculus for monoidal categories. You can see the full paper on the arXiv, or see the slides from a talk I gave about it at CT2017 here. Below the fold, I’ll show you the diagrams and a bit of what you can do with them.
What is a Double Category?
A double category is a category internal to the category of categories. Now, this is fun to say, but takes a bit of unpacking. Here is a more elementary definition together with the string diagrams:
Definition: A double category has
- Objects , , , which will be written as bounded plane regions of different colors
 ,
,  ,
,  , .
, . - Vertical arrows

 , , which we will just call arrows and write as vertical lines
, , which we will just call arrows and write as vertical lines 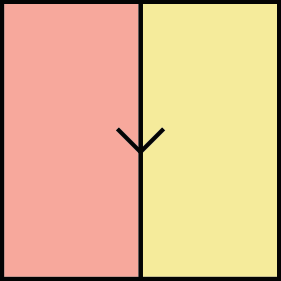 , directed downwards, dividing the plane region
, directed downwards, dividing the plane region  from
from  .
. - Horizontal arrows , ,

 , , which we will just call proarrows and write as horizontal lines
, , which we will just call proarrows and write as horizontal lines  dividing the plane region
dividing the plane region  from
from  .
. - 2-cells
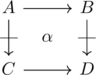 ,, are represented as beads between the arrows and proarrows
,, are represented as beads between the arrows and proarrows 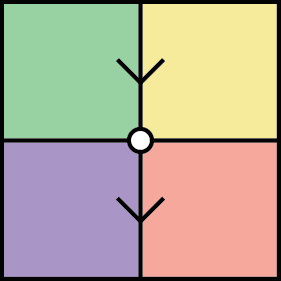 ,
,
The usual square notation is on the left, and the string diagrams are on the right.
There are two ways to compose 2-cells: horizontally, and vertically. These satisfy and interchange law saying that composing horizontally and then vertically is the same as composing vertically and then horizontally.
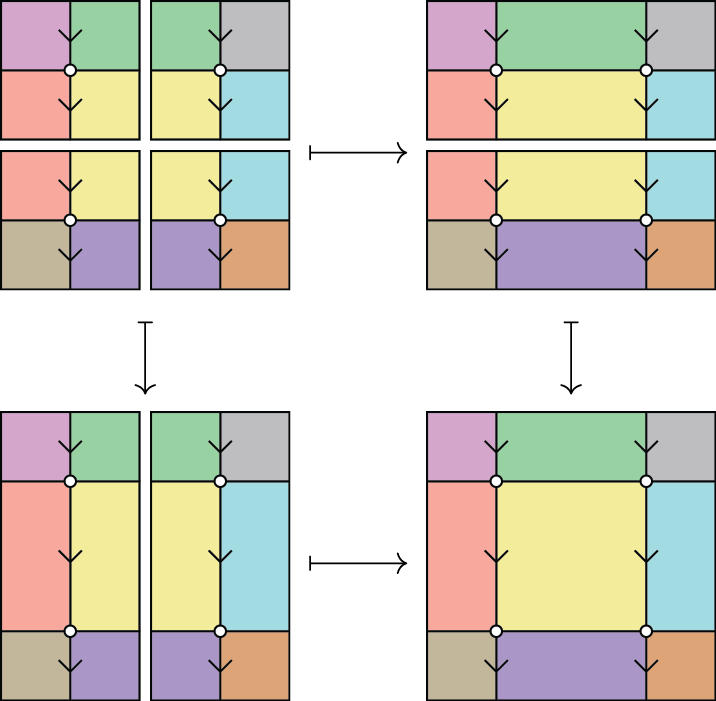
Note that when we compose 2-cells horizontally, we must compose the vertical arrows. Therefore, the vertical arrows will form a category. Similary, when we compose 2-cells vertically, we must compose the horizontal proarrows. Therefore, the horizontal proarrows will form a category. Except, this is not quite true; in most of our examples in the wild, the composition of proarrows will only commute up to isomorphism, so they will form a bicategory. I’ll just hand wave this away for the rest of the post.
This is about all there is to the graphical calculus for double categories. Any deformation of a double diagram that keeps the vertical arrows vertical and the horizontal proarrows horizontal will describe an equal composite in any double category.
Here are some examples of double categories:

In many double categories that we meet “in the wild”, the arrows will be function-like and the proarrows relation-like. These double categories are called equipments. In these cases, we can turn functions into relations by taking their graphs. This can be realized in the graphical calculus by bending vertical arrows horizontal.
Companions, Conjoints, and Equipments
An arrow ![]() has a companion if there is a proarrow
has a companion if there is a proarrow ![]() together with two 2-cells
together with two 2-cells ![]() and
and ![]() such that
such that
![]() =
= ![]() and
and
![]() =
= ![]() .
.
I call these the “kink identities”, because they are reminiscent of the “zig-zag identities” for adjunctions in string diagrams. We can think of ![]() as the graph of
as the graph of ![]() as a subset of its domain times its codomain.
as a subset of its domain times its codomain.
Similarly, ![]() is said to have a conjoint if there is a proarrow
is said to have a conjoint if there is a proarrow ![]() together with two 2-cells
together with two 2-cells ![]() and
and ![]() such that
such that
![]()
![]() and
and ![]()
![]() .
.
Definition: A proarrow equipment is a double category where every arrow has a conjoint and a companion.
The prototypical example of a proarrow equipment, and also the reason for the name, is the equipment of categories, functors, profunctors, and profunctor morphisms. In this equipment, companions are the restriction of the hom of the codomain by the functor on the left, and conjoints are the restriction of the hom of the codomain by the functor on the right.
In the equipment with objects sets, arrows functions, and proarrows relations, the companion and conjoint are the graph of a function as a relation from the domain to codomain or from the codomain to domain respectively.
The following lemma is a central elementary result of the theory of equipments:
Lemma (Spider Lemma): In an equipment, we can bend arrows. More formally, there is a bijective correspondence between diagrams of form of the left, and diagrams of the form of the right:
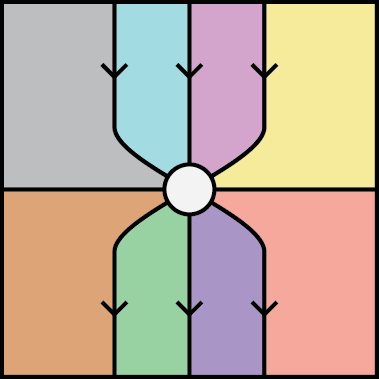
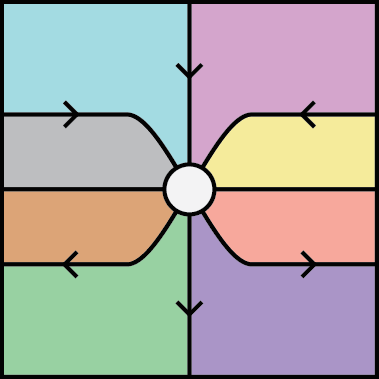 .
.
Proof. The correspondence is given by composing the outermost vertical or horizontal arrows by their companion or conjoint (co)units, as suggested by the slight bends in the arrows above. The kink identities then ensure that these two processes are inverse to each other, giving the desired bijection.
In his post, Mike calls this the “fundamental lemma”. This is the engine humming under the graphical calculus; in short, the Spider Lemma says that we can bend vertical wires horizontal. We can use this bending to prove a classical result of category theory in a very general setting.
Hom-Set and Zig-Zag Adjunctions
It is a classical fact of category theory that an adjunction may be defined using natural transformations and (which we will call a zig-zag adjunction, after the coherence conditions they have to satisfy – also called the triangle equations), or by giving a natural isomorphism . This equivalence holds in any proarrow equipment, which we can now show quickly and intuitively with string diagrams.
Suppose we have an adjunction
![]()
![]() , given by the vertical cells
, given by the vertical cells ![]() and
and ![]() , satisfying the zig-zag identities
, satisfying the zig-zag identities
![]() =
= ![]() and
and ![]() =
= ![]() .
.
By bending the unit and counit, we get the horizontal cells ![]() and
and ![]() . Bending the zig-zag identities shows that these maps are inverse to each other
. Bending the zig-zag identities shows that these maps are inverse to each other
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
and are therefore the natural isomorphism ![]()
![]() we wanted.
we wanted.
Going the other way, suppose ![]() is a natural isomorphism with inverse
is a natural isomorphism with inverse ![]() . That is,
. That is,
![]() =
= ![]() and
and ![]() =
= ![]() .
.
Then we can define a unit ![]() and counit
and counit ![]() by bending. These satisfy the zig-zag identities by pulling straight and using (1):
by bending. These satisfy the zig-zag identities by pulling straight and using (1):
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() .
.
Though this proof can be discovered graphically, it specializes to the usual argument in the case that the equipment is an equipment of enriched categories!
And Much, Much More!
In the paper, you’ll find that every deformation of an equipment diagram gives the same composite – the graphical calculus is sound. But you’ll also find an application of the calculus: a “Yoneda-style” embedding of every equipment into the equipment of categories enriched in it. The paper still definitely needs some work, so I welcome any feedback in the comments!
I hope these string diagrams make using equipments easier and more fun.

Re: A Graphical Calculus for Proarrow Equipments
Cool stuff! Are there any ‘power users’ of proarrow equipments—people who use them a lot?—who might benefit from this technology?
My friend Paul-André Melliès leaps to mind.