The n-Category Café

There are many kinds of networks. You can usually create big networks of a given kind by sticking together smaller networks of this kind. The networks usually do something, and the behavior of the whole is usually determined by the behavior of the parts and how the parts are stuck together.

So, we should think of networks of a given kind as morphisms in a category, or more generally elements of an algebra of some operad, and define a map sending each such network to its behavior. Then we can study this map mathematically!

All these insights (and many more) are made precise in Fong’s theory of ‘decorated cospans’:

• Brendan Fong, The Algebra of Open and Interconnected Systems, Ph.D. thesis, University of Oxford, 2016. (Blog article here.)

Kenny Courser is starting to look at the next thing: how one network can turn into another. For example, a network might change over time, or we might want to simplify a complicated network somehow. If a network is morphism, a process where one network turns into another could be a ‘2-morphism’: that is, a morphism between morphisms. Just as categories have objects and morphisms, bicategories have objects, morphisms and 2-morphisms.

So, Kenny is looking at bicategories. As a first step, Kenny took Brendan’s setup and souped it up to define ‘decorated cospan bicategories’:

• Kenny Courser, Decorated cospan bicategories, to appear in Theory and Applications of Categories.

In this paper, he showed that these bicategories are often ‘symmetric monoidal’. This means that you can not only stick networks together end to end, you can also set them side by side or cross one over the other—and similarly for processes that turn one network into another! A symmetric monoidal bicategory is a somewhat fearsome structure, so Kenny used some clever machinery developed by Mike Shulman to get the job done:

• Mike Shulman, Constructing symmetric monoidal bicategories.

I would love to talk about the details, but they’re a bit technical so I think I’d better talk about something more basic. Namely: what’s a decorated cospan category and what’s a decorated cospan bicategory?

First: what’s a decorated cospan? A cospan in some category $C$ is a diagram like this:

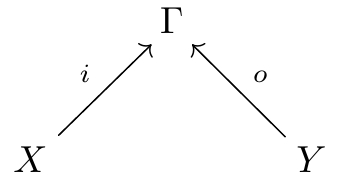
where the objects and morphisms are all in $C.$ For example, if $C$ is the category of sets, we’ve got two sets $X$ and $Y$ mapped to a set $\Gamma.$

In a ‘decorated’ cospan, the object $\Gamma$ is equipped or, as we like to say, ‘decorated’ with extra structure. For example:

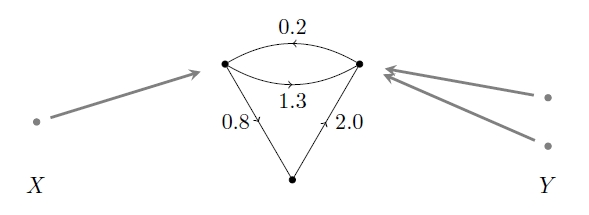
Here the set $\Gamma$ consists of 3 points—but it’s decorated with a graph whose edges are labelled by numbers! You could use this to describe an electrical circuit made of resistors. The set $X$ would then be the set of ‘input terminals’, and $Y$ the set of ‘output terminals’.

In this example, and indeed in many others, there’s no serious difference between inputs and outputs. We could reflect the picture, switching the roles of $X$ and $Y,$ and the inputs would become outputs and vice versa. One reason for distinguishing them is that we can then attach the outputs of one circuit to the inputs of another and build a larger circuit. If we think of our circuit as a morphism from the input set $X$ to the output set $Y,$ this process of attaching circuits to form larger ones can be seen as composing morphisms in a category.

In other words, if we get the math set up right, we can compose a decorated cospan from $X$ to $Y$ and a decorated cospan from $Y$ to $Z$ and get a decorated cospan from $X$ to $Z.$ So with luck, we get a category with objects of $C$ as objects, and decorated cospans between these guys as morphisms!

For example, we can compose this:

and this:

to get this:

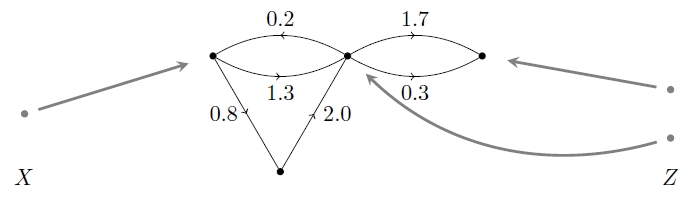
What did I mean by saying ‘with luck’? Well, there’s not really any luck involved, but we need some assumptions for all this to work. Before we even get to the decorations, we need to be able to compose cospans. We can do this whenever our cospans live in a category with pushouts. In category theory, a pushout is how we glue two things together.

So, suppose our category $C$ has pushouts. IF we then have two cospans in $C,$ one from $X$ to $Y$ and one from $Y$ to $Z:$

we can take a pushout:

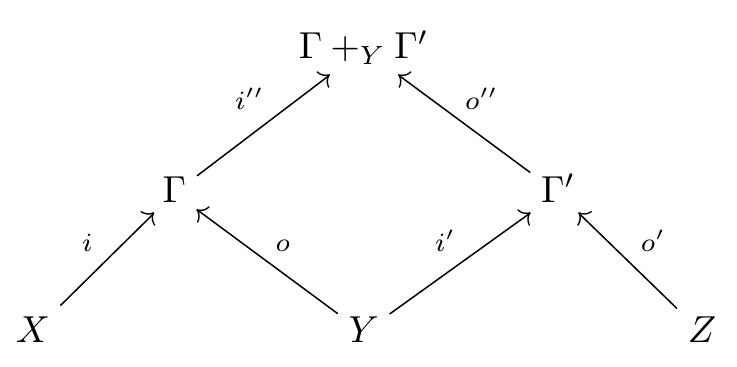
and get a cospan from $X$ to $Z:$

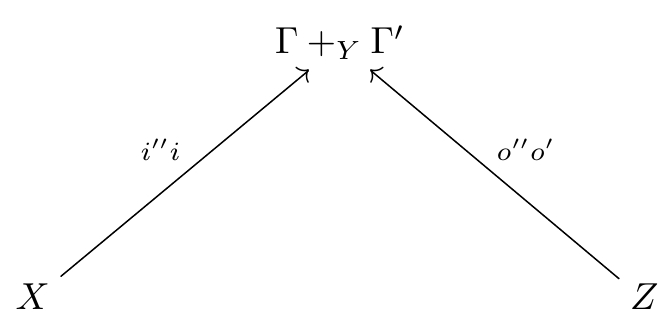
All this is fine and dandy, but there’s a slight catch: the pushout is only defined up to isomorphism, so we can’t expect this process of composing cospans to be associative: it will only be associative up to isomorphism.

What does that mean? What’s an isomorphism of cospans?

I’m glad you asked. A map of cospans is a diagram like this:

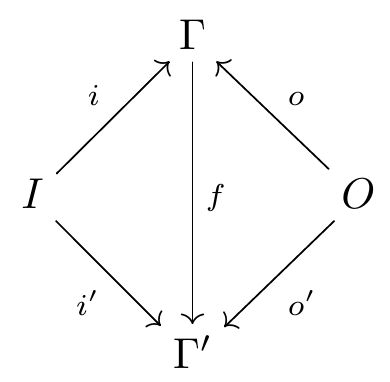
where the two triangles commmute. You can see two cospans in this picture; the morphism $f$ provides the map from one to the other. If $f$ is an isomorphism, then this is an isomorphism of cospans.

To get around this problem, we can work with a category where the morphisms aren’t cospans, but isomorphism classes of cospans. That’s what Brendan did, and it’s fine for many purposes.

But back around 1972, when Bénabou was first inventing bicategories, he noticed that you could also create a bicategory with

• objects of $C$ as objects,
• spans in $C$ as morphisms, and
• maps of spans in $C$ as 2-morphisms.

Bicategories are perfectly happy for composition of 1-morphisms to be associative only up to isomorphism, so this solves the problem in a somewhat nicer way. (Taking equivalence classes of things when you don’t absolutely need to is regarded with some disdain in category theory, because it often means you’re throwing out information—and when you throw out information, you often regret it later.)

So, if you’re interested in decorated cospan categories, and you’re willing to work with bicategories, you should consider thinking about decorated cospan bicategories. And now, thanks to Kenny Courser’s work, you can!

He showed how the decorations work in the bicategorical approach: for example, he proved that whenever $C$ has finite colimits and

$$F : (C,+) \to (\mathrm{Set}, \times)$$

is a lax symmetric monoidal functor, you get a symmetric monoidal bicategory where a morphism is a cospan in $C:$

with the object $\Gamma$ decorated by an element of $F(\Gamma).$

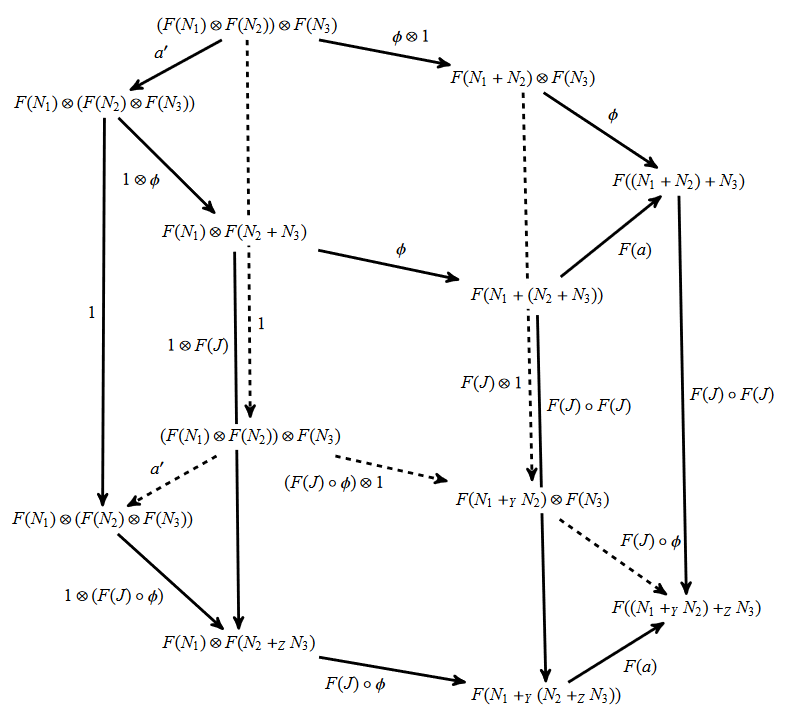
Proving this took some virtuosic work in category theory. The key turns out to be this glorious diagram:

For the explanation, check out Proposition 4.5 in his paper.

I’ll talk more about applications of cospan bicategories when I blog about some other papers Kenny Courser and Daniel Cicala are writing.