Distributive Laws
Posted by Emily Riehl
Guest post by Liang Ze Wong
The Kan Extension Seminar II continues and this week, we discuss Jon Beck’s “Distributive Laws”, which was published in 1969 in the proceedings of the Seminar on Triples and Categorical Homology Theory, LNM vol 80. In the previous Kan seminar post, Evangelia described the relationship between Lawvere theories and finitary monads, along with two ways of combining them (the sum and tensor) that are very natural for Lawvere theories but less so for monads. Distributive laws give us a way of composing monads to get another monad, and are more natural from the monad point of view.
Beck’s paper starts by defining and characterizing distributive laws. He then describes the category of algebras of the composite monad. Just as monads can be factored into adjunctions, he next shows how distributive laws between monads can be “factored” into a “distributive square” of adjunctions. Finally, he ends off with a series of examples.
Before we dive into the paper, I would like to thank Emily Riehl, Alexander Campbell and Brendan Fong for allowing me to be a part of this seminar, and the other participants for their wonderful virtual company. I would also like to thank my advisor James Zhang and his group for their insightful and encouraging comments as I was preparing for this seminar.
First, some differences between this post and Beck’s paper:
I’ll use the standard, modern convention for composition: the composite will be denoted . This would be written in Beck’s paper.
I’ll use the terms “monad” and “monadic” instead of “triple” and “tripleable”.
I’ll rely quite a bit on string diagrams instead of commutative diagrams. These are to be read from right to left and top to bottom. You can learn about string diagrams through these videos or this paper (warning: they read string diagrams in different directions than this post!).
All constructions involving the category of -algebras, , will be done in an “object-free” manner involving only the universal property of .
The last two points have the advantage of making the resulting theory applicable to -categories or bicategories other than , by replacing categories/ functors/ natural transformations with 0/1/2-cells.
Since string diagrams play a key role in this post, here’s a short example illustrating their use. Suppose we have functors and such that . Let be the unit and the counit of the adjunction. Then the composite can be drawn thus:
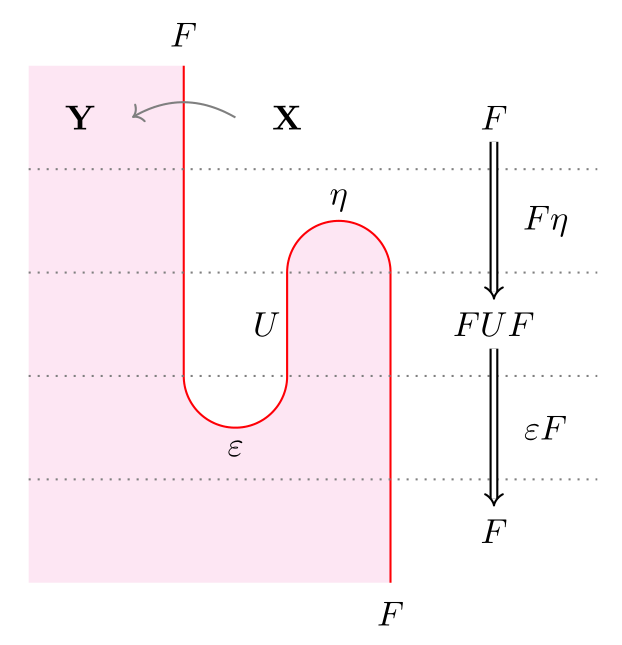
Most diagrams in this post will not be as meticulously labelled as the above. Unlabelled white regions will always stand for a fixed category . If , I’ll use the same colored string to denote them both, since they can be distinguished from their context: above, goes from a white to red region, whereas goes from red to white (remember to read from right to left!). The composite monad (not shown above) would also be a string of the same color, going from a white region to a white region.
Motivating examples
Example 1: Let be the free monoid monad and be the free abelian group monad over . Then the elementary school fact that multiplication distributes over addition means we have a function for a set, sending , say, to . Further, the composition of with is the free ring monad, .
Example 2: Let and be monoids in a braided monoidal category . Then is also a monoid, with multiplication:
where is provided by the braiding in .
In example 1, there is also a monoidal category in the background: the category of endofunctors on . But this category is not braided – which is why we need distributive laws!
Distributive laws, composite and lifted monads
Let and be monads on a category . I’ll use Scarlet and Teal strings to denote and , resp., and white regions will stand for .
A distributive law of over is a natural transformation , denoted
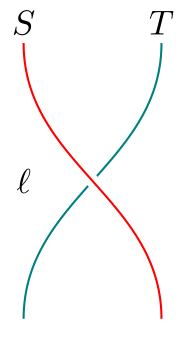
satisfying the following equalities:
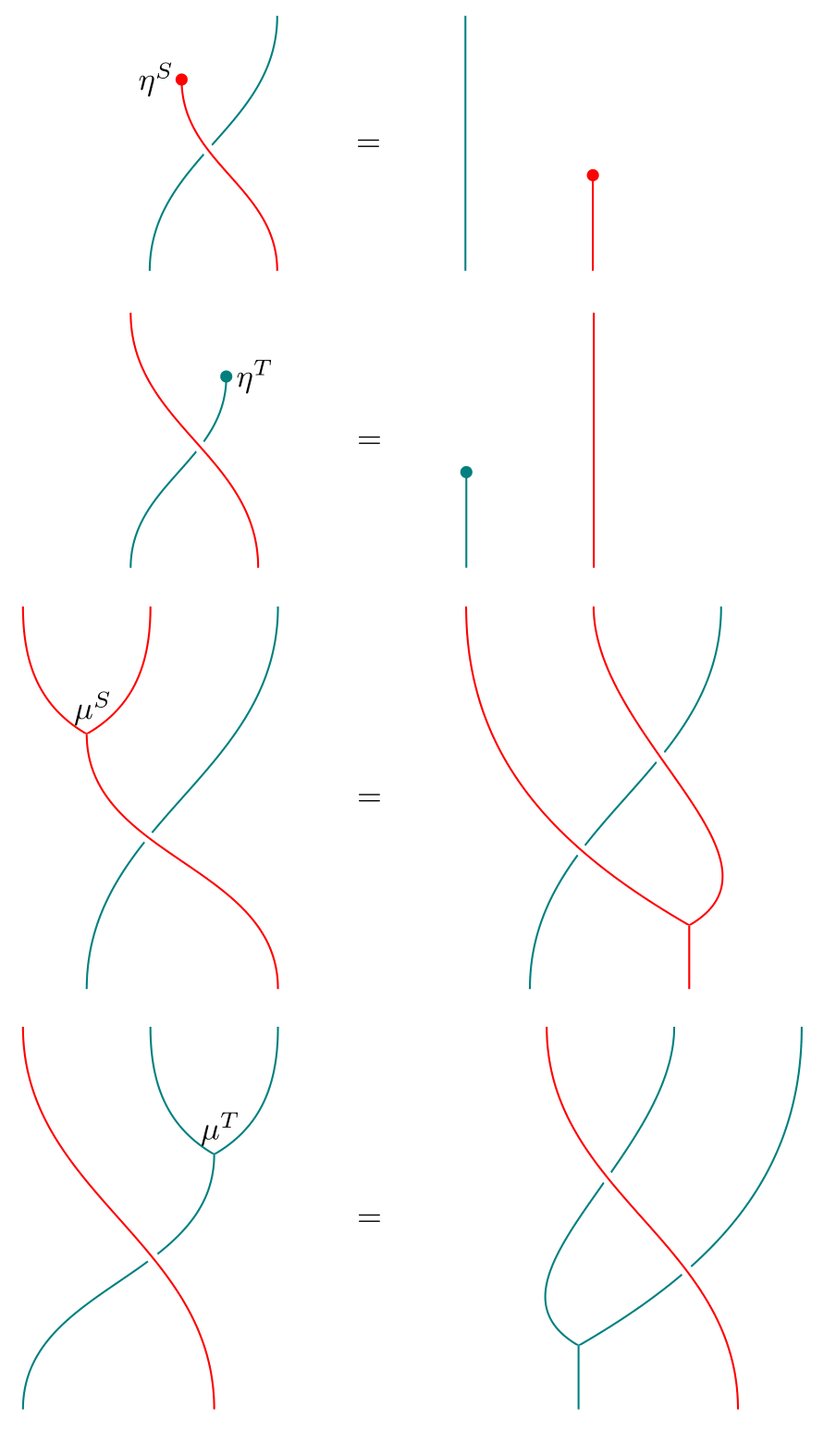
A distributive law looks somewhat like a braiding in a braided monoidal category. In fact, it is a local pre-braiding: “local” in the sense of being defined only for over , and “pre” because it is not necessarily invertible.
As the above examples suggest, a distributive law allows us to define a multiplication :
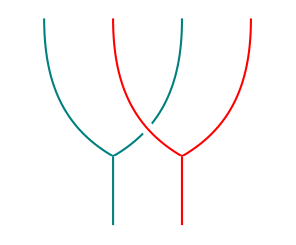
It is easy to check visually that this makes a monad, with unit . For instance, the proof that is associative looks like this:
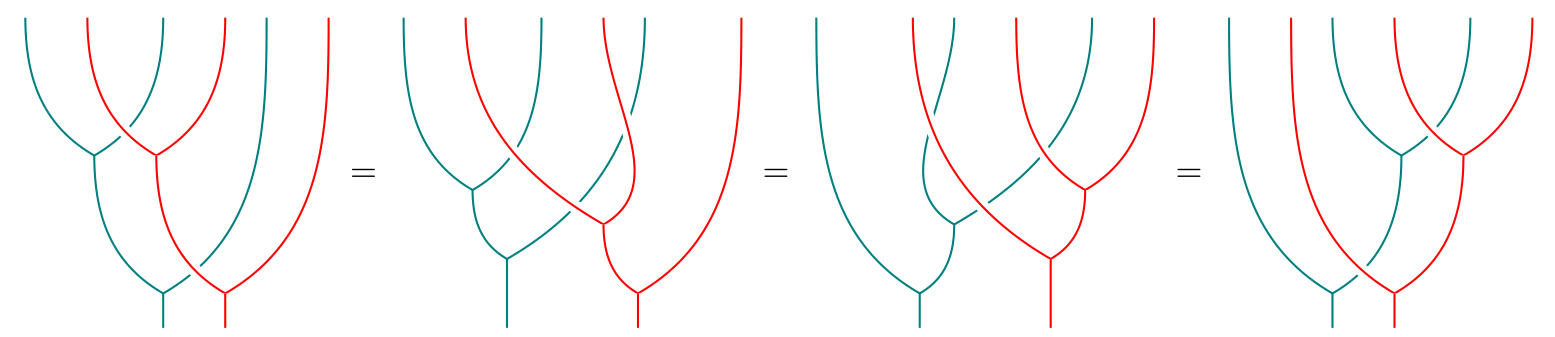
Not only is a monad, we also have monad maps and :
Asserting that is a monad morphism is the same as asserting these two equalities:
Similar diagrams hold for . Finally, the multiplication also satisfies a middle unitary law:
To get back the distributive law, we can simply plug the appropriate units at both ends of :
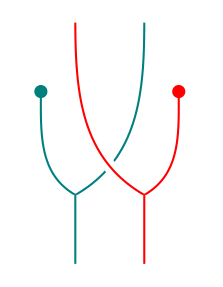
This last procedure (plugging units at the ends) can be applied to any . It turns out that if happens to satisfy all the previous properties as well, then we also get a distributive law. Further, the (distributive law multiplication) and (multiplication distributive law) constructions are mutually inverse:
Theorem The following are equivalent: (1) Distributive laws ; (2) multiplications such that is a monad, and are monad maps, and the middle unitary law holds.
In addition to making a monad, distributive laws also let us lift to the category of -algebras, . Before defining what we mean by “lift”, let’s recall the universal property of : Let be another category; then there is an isomorphism of categories between – the category of functors and natural transformations between them, and - – the category of functors equipped with an -action and natural transformations that commute with the -action.
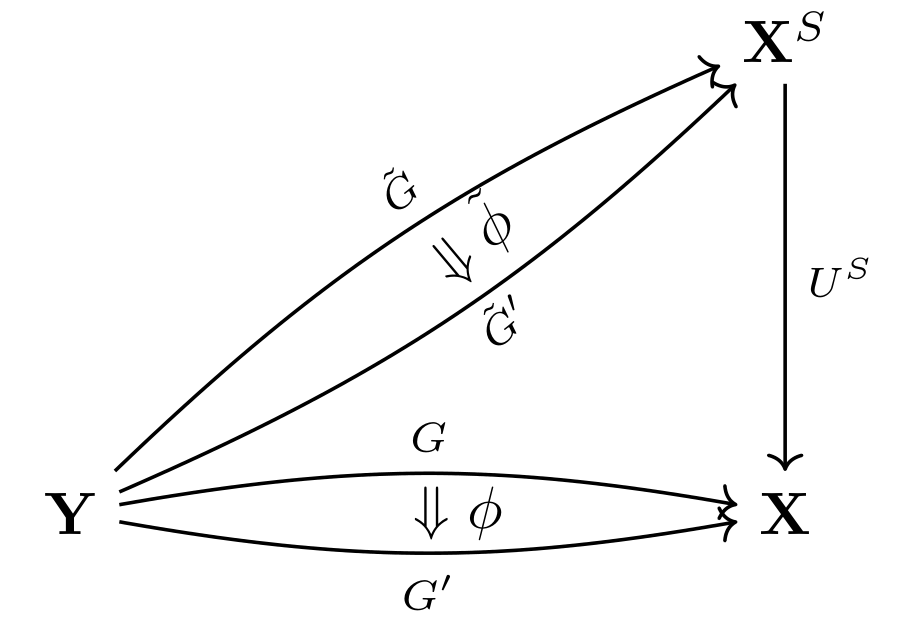
Given , we get a functor by composing with . This composite has an -action given by the canonical action on . The universal property says that every such functor with an -action is of the form . Similar statements hold for natural transformations. We will call and lifts of and , resp.
A monad lift of to is a monad on such that
We may express via the following equivalent commutative diagrams:
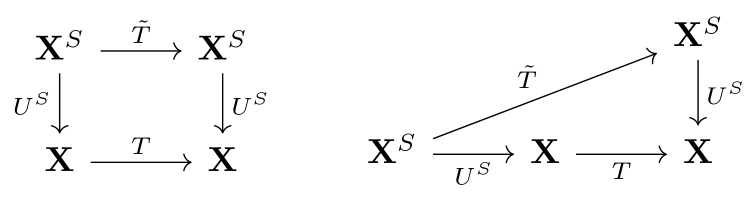
The diagram on the right makes it clear that being a monad lift of is equivalent to being lifts of , resp. Thus, to get a monad lift of , it suffices to produce an -action on and check that it is compatible with and . We may simply combine the distributive law with the canonical -action on to obtain the desired action on :
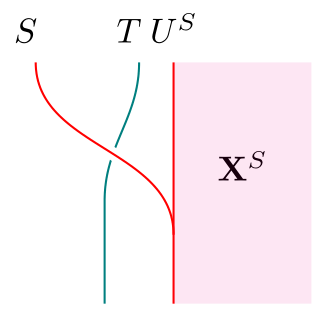
(Recall that the unlabelled white region is . In subsequent diagrams, we will leave the red region unlabelled as well, and this will always be . Similarly, teal regions will denote .)
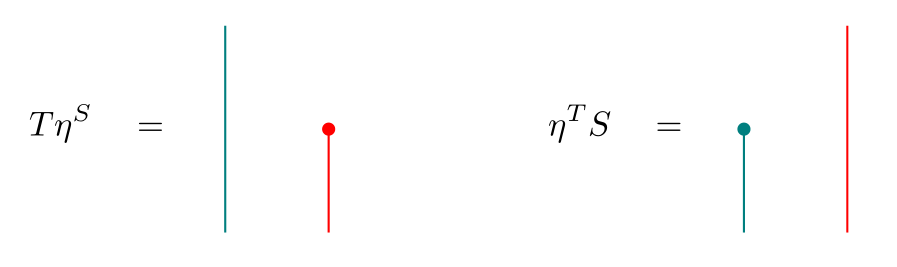
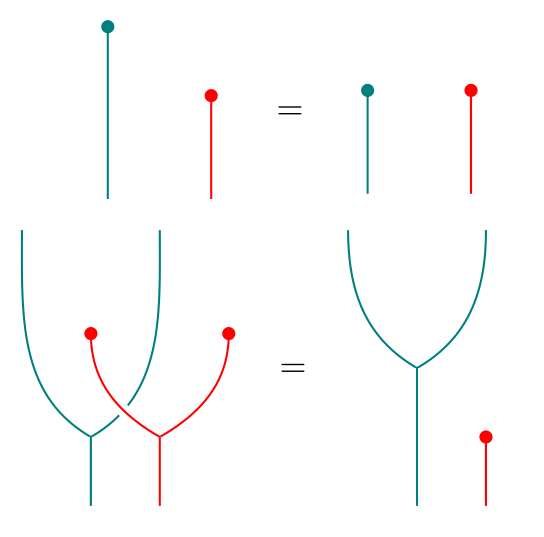
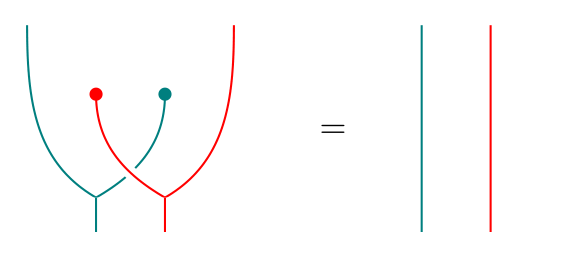
Conversely, suppose we have a monad lift of . Then the equality can be expressed by saying that we have an invertible natural transformation . Using and the unit and counit of the adjunction that gives rise to , we obtain a distributive law of over :
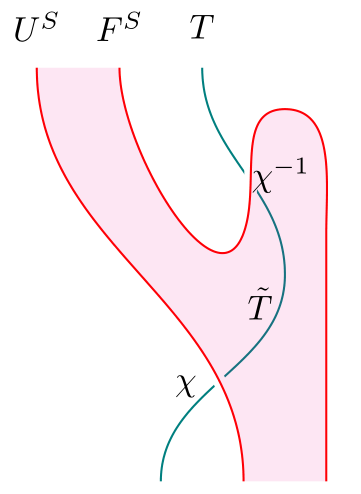
The key steps in the proof that these constructions are mutually inverse are contained in the following two equalities:
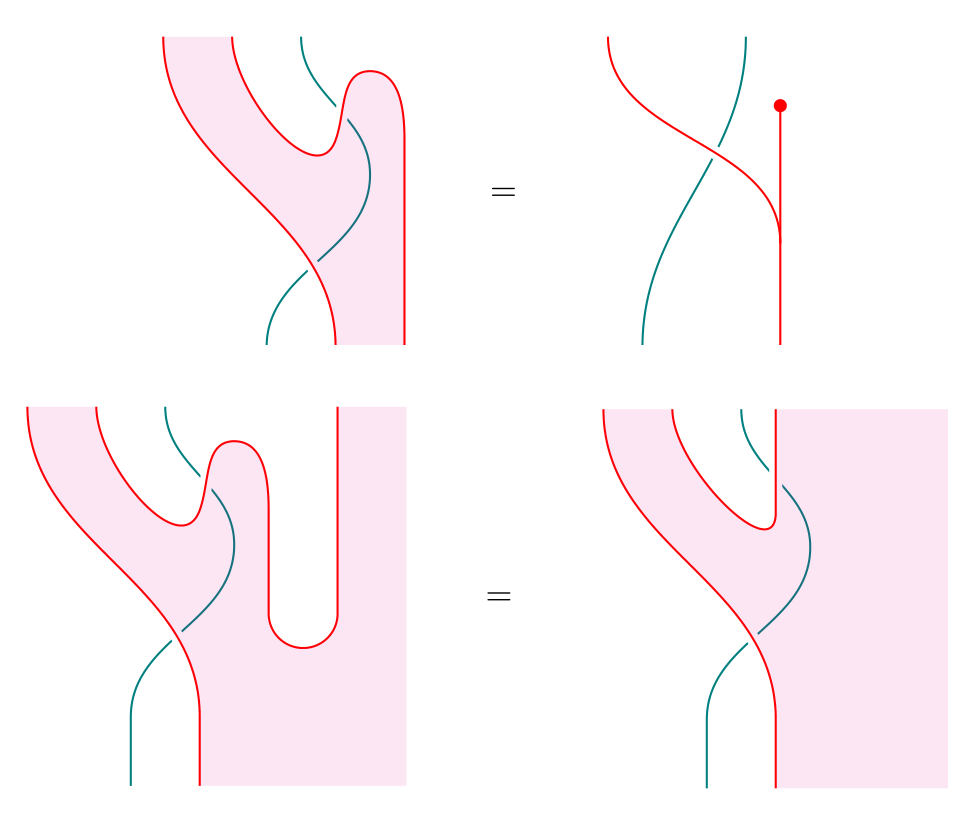
The first shows that the resulting distributive law in the (distributive law monad lift distributive law) construction is the same as the original distributive law we started with. The second shows that in the (monad lift distributive law another lift ) construction, the -action on (LHS of the equation) is the same as the original -action on (RHS), hence (by virtue of being lifts, and can only differ in their induced -actions on ). We thus have another characterization of distributive laws:
Theorem The following are equivalent: (1) Distributive laws ; (3) monad lifts of to .
In fact, the converse construction did not rely on the universal property of , and hence applies to any adjunction giving rise to (with a suitable definition of a monad lift of in this situation). In particular, it applies to the Kleisli adjunction . Since the Kleisli category is equivalent to the subcategory of free -algebras (in the classical sense) in , this means that to get a distributive law of over , it suffices to lift to a monad over just the free -algebras! (Thanks to Jonathan Beardsley for pointing this out!) The resulting distributive law may be used to get another lift of , but we should not expect this to be the same as the original lift unless the original lift was “monadic” to begin with, in the sense of being a lift to .
There are two further characterizations of distributive laws that are not mentioned in Beck’s paper, but whose equivalences follow easily. Eugenia Cheng in Distrbutive laws for Lawvere theories states that distributive laws of over are also equivalent to extensions of to a monad on the Kleisli category . This follows by duality from the above theorem, since . Finally, Ross Street’s The formal theory of monads (which was also covered in a previous Kan Extension Seminar post) says that distributive laws in a -category are precisely monads in . It is a fun and easy exercise to draw string diagrams for objects of ; it becomes visually obvious that these are the same as distributive laws.
Algebras for the composite monad
After characterizing distributive laws, Beck characterizes the algebras for the composite monad .
Just as a morphism of rings induces a “restriction of scalars” functor --, the monad maps and induce functors and .
Equivalently, we have - and -actions on , which we call and . Let be the canonical -action on . The middle unitary law then implies that :
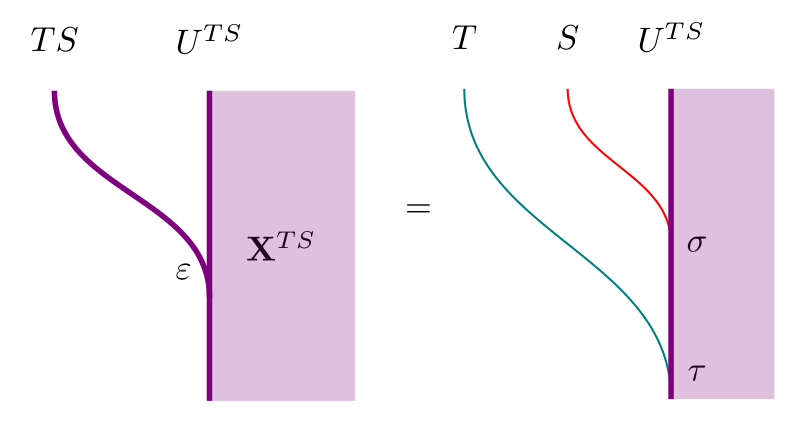
Further, is distributes over in the following sense:
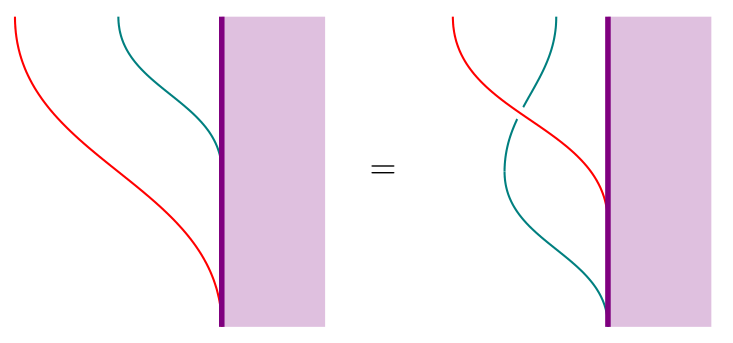
The properties of these actions allow us to characterize -algebras:
Theorem The category of algebras for coincides with that of :
To prove this, Beck constructs and its inverse . These constructions are best summarized in the following diagram of lifts:
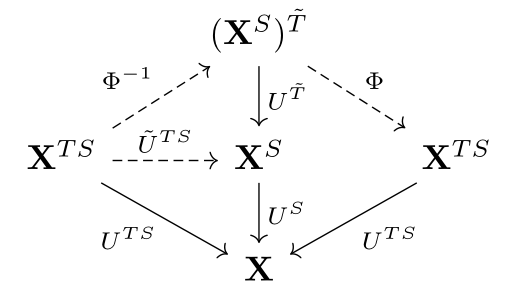
On the left half of the diagram, we see that to get , we must first produce a functor with a -action. We already have as a lift of , given by the -action . We also have the -action on , which distributes over. This is precisely what is required to get a lift of to a -action on , which gives us .
On the right half of the diagram, to get we need to produce a functor with a -action. The obvious functor is , and we get an action by using the canonical actions of on and on :
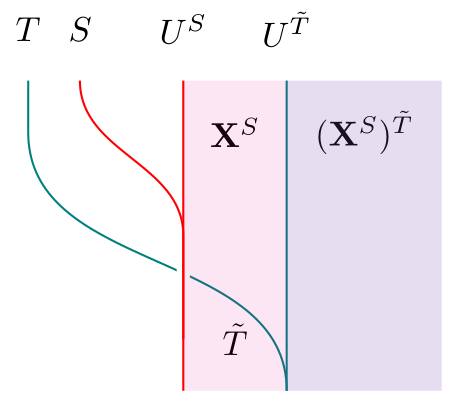
All that’s left to prove the theorem is to check that and are inverses. In a similar fashion, we can prove the dual statement (again found in Cheng’s paper but not Beck’s):
Theorem The Kleisli category of coincides with that of :
Distributivity for adjoints
From now on, we identify with . Under this identification, it turns out that , and we obtain what Beck calls a distributive adjoint situation comprising 3 pairs of adjunctions:
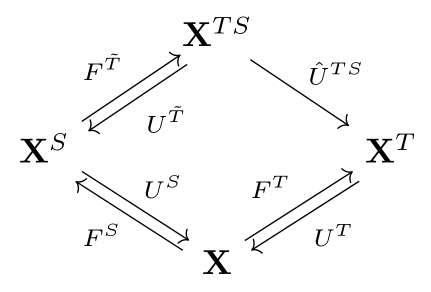
For this to qualify as a distributive adjoint situation, we also require that both composites from to are naturally isomorphic, and both composites from to are naturally isomorphic. This can be expressed in the following diagram by requiring both blue circles to be mutually inverse, and both red circles to be mutually inverse:
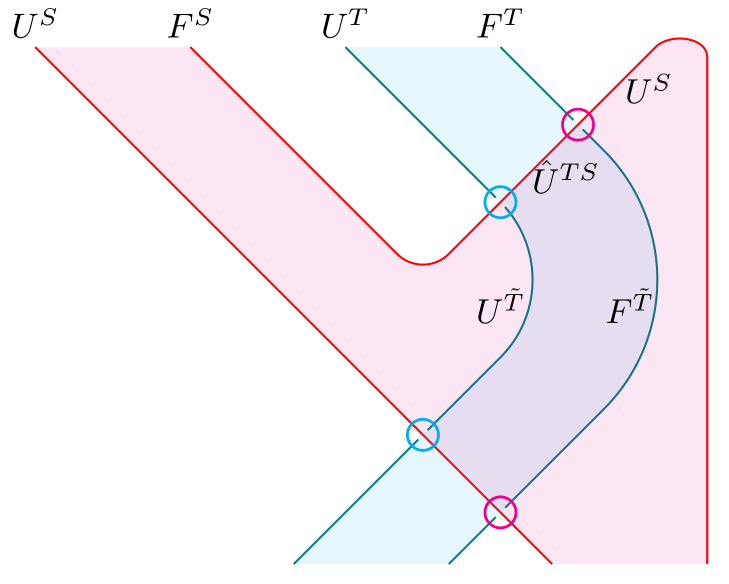
(Recall that colored regions are categories of algebras for the corresponding monads, and the cap and cup are the unit and counit of .)
This diagram is very similar to the diagram for getting a distributive law out of a lift , and it is easy to believe that any such distributive adjoint situation (with 3 pairs of adjoints - not necessarily monadic - and the corresponding natural isomorphisms) leads to a distributive law.
Finally, suppose the “restriction of scalars” functor has an adjoint. This adjoint behaves like an “extension of scalars” functor, and Beck fittingly calls it at the start of his paper. I’ll use instead, to highlight its relationship with .
In such a situation, we get an adjoint square consisting of 4 pairs of adjunctions. By drawing these 4 adjoints in the following manner, it becomes clear which natural transformations we require in order to get a distributive law:
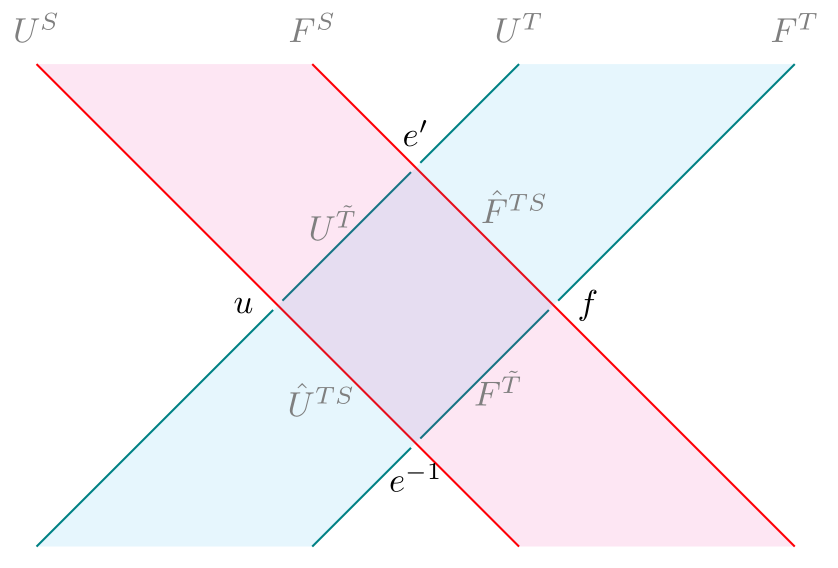
(Recall that and , so this is a “thickened” version of what a distributive law looks like.)
It turns out that given the natural transformation between the composite right adjoints and , we can get the natural transformation as the mate of between the corresponding composite left adjoints and . Note that is invertible if and only if is. We may use or , along with the units and counits of the relevant adjunctions, to construct :
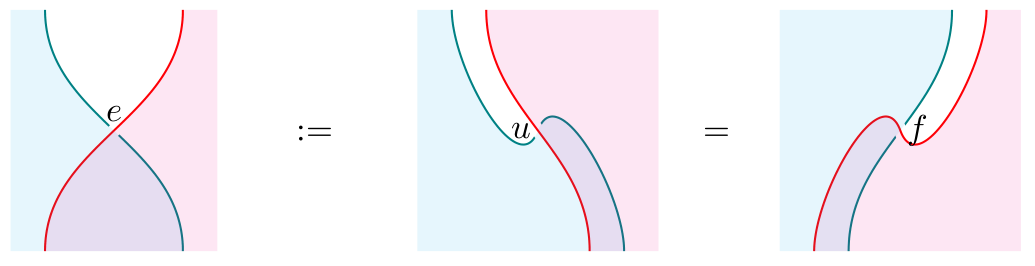
But is in the wrong direction, so we have to further require that is invertible, to get . We get from or in a similar manner. Since will turn out to already be in the right direction, we will not require it to be invertible. Finally, given any 4 pairs of adjoints that look like the above, along with natural transformations satisfying the above properties, we will get a distributive law!
What next?
Beck ends his paper with some examples, two of which I’ve already mentioned at the start of this post. During our discussion, there were some remarks on these and other examples, which I hope will be posted in the comments below. Instead of repeating those examples, I’d like to end by pointing to some related works:
Since we’ve been talking about Lawvere theories, we can ask what distributive laws look like for Lawvere theories. Cheng’s Distributive laws for Lawvere theories, which I’ve already referred to a few times, does exactly that. But first, she comes up with 4 settings in which to define Lawvere theories! She also has a very readable introduction to the correspondence between Lawvere theories and finitary monads.
As Beck mentions in his paper, we can similarly define distributive laws between comonads, as well as mixed distributive laws between a monad and a comonad. Just as we can define bimonoids/bialgebras, and thus Hopf monoids/algebras, in a braided monoidal category, such distributive laws allow us to define bimonads and Hopf monads. There are in fact two distinct notions of Hopf monads: the first is described in this paper by Alain Bruguières and Alexis Virelizier (with a follow-up paper coauthored with Steve Lack, and a diagrammatic approach with amazing surface diagrams by Simon Willerton); the second is this paper by Bachuki Mesablishvili and Robert Wisbauer. The difference between these two approaches is described in the Mesablishvili-Wisbauer paper, but both involve mixed distributive laws. Gabriella Böhm also recently gave a talk entitled The Unifying Notion of Hopf Monad, in which she shows how the many generalizations of Hopf algebras are just instances of Hopf monads (in the first sense) in an appropriate monoidal bicategory!
We also saw that distributive laws are monads in a category of monads. Instead of thinking of distributive laws as merely a means of composing monads, we can study distributive laws as objects in their own right, just as monoids in a category of monoids (a.k.a. abelian monoids) are studied in their own right! The story for monoids terminates at this step: monoids in abelian monoids are just abelian monoids. But for distributive laws, we can keep going! See Cheng’s paper on Iterated Distributive Laws, where she shows the connection between iterated distributive laws and -categories. In addition to requiring distributive laws between each pair of monads involved, it is also necessary to have a Yang-Baxter equation between every three monads:
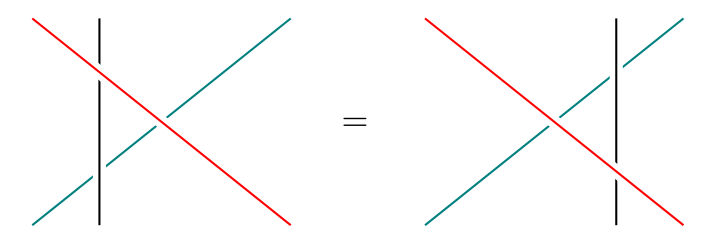
- Finally, there seems to be a strange connection between distributive laws and factorization systems (e.g. here, here and even in “Distributive Laws for Lawvere theories” mentioned above). I can’t say more because I don’t know much about factorization systems, but hopefully someone else can say something illuminating about this!

Re: Distributive Laws
Thanks Ze for a great post! I felt like I’ve gained something from seeing the commutative diagrams presented as string diagrams, in particular the intuition of distributive laws as local non-invertible braidings.
This makes me wonder if in the past I’ve paid too much heed to shapes of diagrams. For instance, if I were to describe the distributive law axioms to another category theorist but couldn’t be bothered to spell them out, I’d say that a distributive law between two monads and on the same object is given by a 2-cell satisfying two triangles involving the units of the monads and two pentagons involving the multiplications of the monads.
My question: do the shapes of these commutative diagrams (the fact that two involve three morphisms and the other two involve five) have any significance?