The n-Category Café

Replacing finite limits

To find a suitable class of limits to replace finite products, we require the concept of presentability. The best entry point is to learn about local finite presentability, which David Myers has discussed here. With a little modification to the ideas there, we define a notion of local strong finite presentability and local $\Phi$-presentability for a class of limits $\Phi$.

We begin with sifted colimits, which are those $\mathbf{Set}$-valued colimits that commute with finite products. Note the familiarity of this definition with the commutativity property of filtered colimits. Of course, filtered colimits are also sifted. Another example is a reflexive pair, that is a category with shape

Anyway, we now look at the strongly finitely presentable objects in a category $\mathbf{C}$. These are those objects $x$ whose representable $\mathbf{C}(x,-) \colon \mathbf{C} \to \mathbf{Set}$ preserves sifted colimits. Denote the full subcategory of these by $\mathbf{C}_{\text{sfp}}$. Some simple examples include $\mathbf{Set}_{\text{sfp}}$, which consists of the finite sets, and $\mathbf{Ab}_{\text{sfp}}$, which has the free and finitely generated Abelian groups. Also, given a category $\mathbf{C}$ of models for a Lawvere theory, $\mathbf{C}_{\text{sfp}}$ is exactly those finitely presentable objects that are regular projective. A category $\mathbf{C}$ is locally strongly finitely presentable if it is cocomplete, $\mathbf{C}_{\text{sfp}}$ is small, and any $\mathbf{C}$-object is a sifted colimit of a diagram in $\mathbf{C}_{\text{sfp}}$. There is also a nice characterization (Theorem 3.1 in the paper) that states $\mathbf{C}$ is locally strongly finitely presentable if and only if $\mathbf{C}_{\text{sfp}}$ has finite coproducts and we can identity $\mathbf{C}$ with the category of finite product-preserving functors $\mathbf{C}^{\text{op}}_{\text{sfp}} \to \mathbf{Set}$. One of the most important results of Notions of Lawvere Theory, was in expanding the theory to encompass sifted (weighted) colimits. More on this later.

We can play this game with any class of limits $\Phi$. Before defining $Phi$-presentability, here is a bit of jargon.

Definition. A functor is $\Phi$-flat if its colimit commutes with $\Phi$-limits.

We call an object $x$ of a category $\mathbf{C}$ $\Phi$-presentable if $\mathbf{C}(x,-) \colon \mathbf{C} \to \mathbf{Set}$ preserves $\Phi$-flat colimits. Given the full subcategory $\mathbf{C}_\Phi$ of $\Phi$-presentable objects, we call $\mathbf{C}$ locally $\Phi$-presentable if it is cocomplete, $\mathbf{C}_{\Phi}$ is small, and any $\mathbf{C}$-object is a $\Phi$-flat colimit of a diagram in $\mathbf{C}_{\Phi}$. Fortunately, we retain the characterization of $\mathbf{C}$ being locally $\Phi$-presentable if and only if $\mathbf{C}_{\Phi}$ has $\Phi$-colimits and $\mathbf{C}$ is equivalent to the category $\Phi$-$\mathbf{Cts}(\mathbf{C}^{\text{op}}_\Phi, \mathbf{Set})$ of $\Phi$-continuous functors $\mathbf{C}^{\text{op}}_\Phi \to \mathbf{Set}$. Important results in Notions of Lawvere Theory use the assumption of $\Phi$-presentability.

Let’s come back to Lawvere theories. From this point on, we fix a symmetric monoidal closed category $\mathcal{V}$ that is both complete and cocomplete. Also, $\Phi$ will refer to a class of weights over $\mathcal{V}$. Our first task will be to determine what class of limits can replace finite products in the classical case. To this end, we take the following assumption.

Axiom A. $\Phi$-continuous weights are $\Phi$-flat.

This axiom is an analogy with how filtered colimits commute with finite limits in $\mathbf{Set}$. But for what classes of limits $\Phi$ does this hold?

To answer this question, we fix a sound doctrine $\mathbb{D}$. Very roughly, a sound doctrine is a collection of small categories whose limits behave nicely with respect to certain colimits. After putting some small assumptions on the underlying category $\mathcal{V}_0$ which we’ll sweep under the rug, define $\mathcal{V}_\mathbb{D}$ to be the full sub $\mathcal{V}$-category consisting of those objects $x$ such that $[x,-] \colon \mathcal{V} \to \mathcal{V}$ preserves $\mathbb{D}$-flat colimits. Let $\Phi$ be the class of limits ‘built from’ conical $\mathbb{D}$-limits and $\mathcal{V}_\mathbb{D}$-powers in the sense that we take $\phi \in \Phi$ if

• any $\mathcal{V}$-category with conical $\mathbb{D}$ limits and $\mathcal{V}_\mathbb{D}$-powers also admits $\phi$-weighted limits, and

• any $\mathcal{V}$-functor conical $\mathbb{D}$ limits and $\mathcal{V}_\mathbb{D}$-powers also preserves $\phi$-weighted limits.

The fancy way of saying this is that $\Phi$ is the saturation class of conical $\mathbb{D}$-limits and $\mathcal{V}_\mathbb{D}$-powers. It’s easy enough to see that $\Phi$ contains the conical $\mathbb{D}$-limits and $\mathcal{V}$-powers.

Having constructed a class of limits $\Phi$ from a sound doctrine $\mathbb{D}$, we use the following theorem to imply that $\Phi$ satisfies the axiom above.

Theorem. Let $\mathcal{K}$ be a small $\mathbf{V}$-category with $\Phi$-weighted limits and $F \colon \mathcal{K} \to \mathcal{V}$ be a $\mathbf{V}$-functor. The following are equivalent:

• $F$ is $\mathbb{D}$-continuous;

• $F$ is $\Phi$-flat

• $F$ is $\Phi$-continuous.

In particular, the first item allows us to construct $\Phi$ using sound limits and the equivalence between the second and third item is precisely the axiom of interest. Here are some examples.

Example. Let $\mathbb{D}$ be the collection of all finite categories. We will also take $\mathcal{V}_0$ be locally finitely presentable with the additional requirement that the monoidal unit $I$ is finitely presentable as is the tensor product of two finitely presentable objects. Examples of such a $\mathcal{V}$ are categories of sets, abelian groups, modules over a commutative ring, chain complexes, categories, groupoids, and simplicial sets. Then $\Phi$, as constructed from $\mathbb{D}$ above gives a good notion of $\mathcal{V}$-enriched finite limits.

Example. A second example, and one of the main contributions of Notions of Lawvere Theory is when $\mathbb{D}$ is the class of all finite, discrete categories. Here, we take our $\mathcal{V}$ as in the first example, though we do not require the monoidal unit to be strongly finitely presentable. We do this because, by requiring the monoidal unit to be strongly finitely presentable, we lose the example where $\mathcal{V}$ is the category of directed graphs, which happens to be a key example, particularly to realizing categories as an model of a Lawvere theory. In this case, the induced class $\Phi$ gives an enriched version of strongly finite limits as discussed above. This $\Phi$ generalizes finite products in the sense that they coincide when $\mathcal{V}$ is $\mathbf{Set}$.

Correspondence between Lawvere theories and monads

Now that we’ve gotten our hands on some suitable limits, let’s see how we can obtain the classical correspondence between Lawvere theories and monads. Naturally, we’ll be assuming axiom A. In addition, we fix a $\mathcal{V}$-category $\mathcal{K}$ that satisfies the following.

Axiom B1. $\mathcal{K}$ is locally $\Phi$-presentable.

This axiom implies, as in our discussions above, that $\mathcal{K} \cong \Phi$-$\mathbf{Cts}(\mathcal{K}^{\text{op}}_\Phi,\mathcal{V})$. This is not particularly restrictive, as presheaf $\mathcal{V}$-categories are locally $\Phi$-presentable.

Now, define a Lawvere $\Phi$-theory on $\mathcal{K}$ to be a bijective-on-objects $\mathbf{V}$-functor $g\colon \mathcal{K}^{\text{op}}_{\Phi} \to \mathcal{L}$ that preserves $\Phi$-limits. A striking difference between a Lawvere $\Phi$-theory and the classical notion is that the former does not require $\mathcal{L}$ to have the limits under consideration. This makes defining the models of a Lawvere $\Phi$-theory a subtler issue than in the classical case. Instead of defining a model to be a $\Phi$-continuous functor as one might expect, we instead use the pullback square

To understand what a model looks like, use the intuition for a pullback in the category $\mathbf{Set}$ and the fact that $\mathcal{K}$ is equivalent to $\Phi$-$\mathbf{Cts}(\mathcal{K}^{\text{op}}_\Phi,\mathcal{V})$. So a model will be a $\mathcal{V}$-functor $\mathcal{L} \to \mathcal{V}$ whose restriction along $g$ is $\Phi$-continuous.

The other major player in this section is the category of $\Phi$-flat monads $\mathbf{Mnd}_{\Phi}(\mathcal{K})$. We claim that there is an equivalence between $\mathbf{Law}_{\Phi}(\mathcal{K})$ and $\mathbf{Mnd}_{\Phi}(\mathcal{K})$. To verify this, we construct a pair of functors between $\mathbf{Law}_{\Phi}(\mathcal{K})$ and $\mathbf{Mnd}_{\Phi}(\mathcal{K})$. The first under consideration: ${mnd} \colon \mathbf{Law}_{\Phi}(\mathcal{K}) \to \mathbf{Mnd}_{\Phi}(\mathcal{K})$. We define this with the help of the following proposition.

Proposition. The functor $u$ from the above pullback diagram is monadic via a $\Phi$-flat monad $t$.

Hence, a $\Phi$-theory $\mathcal{L}$ gives a monadic functor $u \colon \mathbf{Mod}(\mathcal{L}) \to \mathcal{K}$ that yields a monad $t$ on $\mathcal{K}$. Moreover, this monad preserves all the limits required to be an object in $\mathbf{Mnd}_\Phi (\mathcal{K})$. So, define ${mnd} (\mathcal{L}) = t$.

Next, we define a functor ${th} \colon \mathbf{Mnd}_{\Phi}(\mathcal{K}) \to \mathbf{Law}_{\Phi}(\mathcal{K})$. Consider a monad $t$ in $\mathbf{Mnd}_{\Phi}(\mathcal{K})$. As per usual, $t$ factors through the Eilenberg-Moore category $\mathcal{K} \to \mathcal{K}^t$ which we precompose with the inclusion $\mathcal{K}_\Phi \to \mathcal{K}$ giving $f \colon \mathcal{K}_\Phi \to \mathcal{K}^m$. Now defining a $\mathcal{V}$-category $\mathcal{G}$ that has objects from $\mathcal{K}_\Phi$ and $\mathcal{G}(x,y) = \mathcal{K}^m(fx,fy)$, we factor $f$

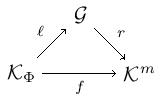
where $\ell$ is bijective-on-objects and $r$ is full and faithful. This factorization is unique up to unique isomorphism. Define $\text{th} (t) = \mathcal{G}^{\text{op}}$.

At this point, we have functors $$\text{mnd} \colon \mathbf{Law}_{\Phi}(\mathcal{K}) \to \mathbf{Mnd}_{\Phi}(\mathcal{K}) \quad \text{ and } \quad \text{th} \colon \mathbf{Mnd}_{\Phi}(\mathcal{K}) \to \mathbf{Law}_{\Phi}(\mathcal{K})$$ so let’s turn our attention to showing that these are mutual weak inverses. The first step is to show that the category of algebras $\mathcal{K}^t$ for a given monad $t$ is the category of models $\mathbf{Mod}(\text{th} (t))$.

Theorem 6.6. The $\mathcal{V}$-functor $$\mathcal{K}^t(r-,-) \colon \mathcal{K}^t \to [\text{th} (t)^{\text{op}},\mathcal{V}], \quad x \mapsto \mathcal{K}^m(r-,x)$$ restricts to an isomorphism of $\mathcal{V}$-categories $\mathcal{K}^t \cong \mathbf{Mod}(\text{th} (t))$.

This theorem gives us that $\text{mnd} \circ \text{th} \cong \text{id}$. The next theorem gives us the other direction.

Theorem 6.7. There is an isomorphism $\text{th} \circ \text{mnd} \cong \text{id}$.

Let’s sketch the proof. Let $g \colon \mathcal{K}^{\text{op}}_{\Phi} \to \mathcal{L}$ be a Lawvere $\Phi$-theory. If we denote $\text{mnd} (\mathcal{T})$ by $t$, we get $\text{th} \circ \text{mnd} (\mathcal{T}) = \text{th} (t) = \mathcal{G}^{\text{op}}$ via the factorization

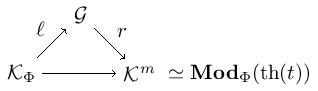
where $\ell$ is bijective-on-objects and $r$ is fully faithful. It remains to show that $\mathcal{T} = \mathcal{G}^{\text{op}}$.
Let’s compute the image of an $\mathcal{K}_\Phi$-object $x$ in $\mathbf{Mod}_{\Phi} (\text{th} (t))$. For this, recall that we have $\mathcal{K} \simeq \Phi$-$\mathbf{Cts}(\mathcal{K}^{\text{op}}_{\Phi},\mathcal{V})$ by assumption. Embedding $x$ into $\Phi$-$\mathbf{Cats}(\mathcal{K}_{\Phi},\mathcal{V})$ gives us $$\mathcal{K}_\Phi(-,x) \colon \mathcal{K}^{\text{op}}_{\Phi} \to \mathcal{V}.$$ This, in turn, is mapped to the left Kan extension $$\text{Lan}_g (\mathcal{K}_\Phi(-,x)) \colon \mathcal{T} \to \mathcal{V}$$ along $g \colon \mathcal{K}^{\text{op}}_{\Phi} \to \mathcal{T}$ (the Lawvere $\Phi$ theory we began with). Here, we can compute that $\text{Lan}_g (\mathcal{K}_\Phi(-,x))$ is $\mathcal{T}(-,gx)$ meaning the factorization above is

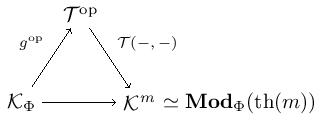
Therefore, $\mathcal{T} = \mathcal{G}^{\text{op}}$ as desired.

Many-sorted theories

Moving from single-sorted to many-sorted theories, we will take a different assumption on our $\mathcal{V}$-category $\mathcal{K}$.

Axiom B2. $\mathcal{K}$ is a $\mathcal{V}$-category with $\Phi$-limits and such that the Yoneda inclusion $\mathcal{K} \to [\mathcal{K}^{\text{op}} , \mathcal{V}]$ has a $\Phi$-continuous left adjoint.

This requirement on $\mathcal{K}$ is not overly restrictive as it holds for all presheaf $\mathcal{V}$-categories and all Grothendieck topoi when $\mathcal{V}$ is $\mathbf{Set}$. The nice thing about this assumption is that we can compute all colimits and $\Phi$-limits in $\mathcal{K}$ by passing to $[\mathcal{K}^{\text{op}} , \mathcal{V}]$, where they commute, then reflecting back.

Generalizing Lawvere theories here is a bit simpler than in the previous section. Indeed, call any small $\mathcal{V}$-category $\mathcal{L}$ with $\Phi$-limits a $\Phi$-theory. Notice that we no longer have a bijective-on-objects functor involved in the definition. That functor forced the single-sortedness. With the functor no longer constraining the structure, we have the possibility for many sorts. Also, a $\Phi$-theory does have all $\Phi$-limits here, unlike in the single-sorted case. This allows for a much simpler definition of a model. Indeed, the category of models for a $\Phi$-theory $L$ is the full subcategory $\Phi$-$\mathbf{Cts}(\mathcal{L}, \mathcal{K})$ of $[\mathcal{L}, \mathcal{K}]$.

Presently, we are interested in generalizing two important properties of Lawvere theory to $\Phi$-theories. The first is that algebraic functors have left adjoints. The second is the reflectiveness of models.

Algebraic functors have left adjoints. A morphism of $\Phi$-theories is a $\Phi$-continuous $\mathcal{V}$-functor $g \colon \mathcal{L} \to \mathcal{L}\prime$. Any such morphism induces a pullback $\mathcal{V}$-functor $g^{\ast} \colon \Phi$-$\mathbf{Cts}(\mathcal{L}\prime, \mathcal{K}) \to \Phi$-$\mathbf{Cts}(\mathcal{L}, \mathcal{K})$ between model $\mathcal{V}$-categories. We call such functors $\Phi$-algebraic. And yes, these do have left adjoints just as in the context of classical Lawvere theories.

Theorem. Let $\mathcal{L}$ and $\mathcal{L}\prime$ be $\Phi$-theories and $g \colon \mathcal{L} \to \mathcal{L}\prime$ a $\mathcal{V}$-functor between them. Given a model $m \colon \mathcal{L} \to \mathcal{K}$, then $\text{Lan}_g m \colon \mathcal{L}\prime \to \mathcal{K}$ is a model.

What is happening here? Of course, pulling back by $g$ gives a way to turn models of $\mathcal{L}\prime$ into models of $\mathcal{L}$ – this is the algebraic functor $g^{\ast}$. But the left Kan extension along $g$ gives a way to turn a model $m$ of $\mathcal{L}$ into a model of $\mathcal{L}\prime$ as depicted in the diagram

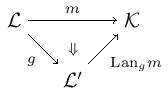
This theorem says that process gives a functor $g_{\ast} \colon \Phi$-$\mathbf{Cts}(\mathcal{L}, \mathcal{K}) \to \Phi$-$\mathbf{Cts}(\mathcal{L}\prime, \mathcal{K})$ given by $m \mapsto \text{Lan}_g m$.

We can prove this theorem for $\mathcal{K} = \mathcal{V}$ without requiring axiom B2. This axiom is used to extend this result to a $\mathcal{V}$-category $\mathcal{K}$. The existence of the left adjoint $\ell$ to the Yoneda embedding $y$ of $\mathcal{K}$ gives a factorization $\text{Lan}_g m = \ell \text{Lan}_g y m$. The proof then reduces to showing that $\text{Lan}_g y m$ is $\Phi$-continuous, since we are already assuming that $\ell$ is. But because the codomain of $\text{Lan}_g y m$ is $[\mathcal{K}^{\text{op}},\mathcal{V}]$, we can rest on the fact that we have proven the result for $\mathcal{K} = \mathcal{V}$. Limits are taken pointwise, after all. Actually, the left adjoint to $g^{\ast}$ holds more generally, but our assumptions on $\mathcal{K}$ allow us to explicitly compute the left adjoint with left Kan extensions.

Reflexiveness of models. Having discussed left adjoints of algebraic functors, we now move on to show that categories of models $\Phi$-$\mathbf{Cts}(\mathcal{T},\mathcal{V})$ are reflexive in $[\mathcal{T}, \mathcal{V}]$. Consider the free-forgetful (ordinary) adjunction

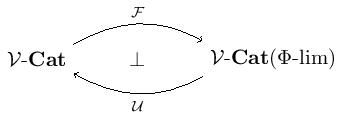
between $\mathcal{V}$-categories and those $\mathcal{V}$-categories with $\Phi$-limits and functors preserving them. Given a $\mathcal{V}$-category $\mathcal{L}$ in the image of $U$. Note that $\mathcal{L}$ is a $\Phi$-theory. It follows from this adjunction that $\Phi$-$\mathbf{Cts}(\mathcal{FL},\mathcal{V})$ is equivalent to the category $[\mathcal{L},\mathcal{V}]$. Moreover, since $\mathcal{L}$ has $\Phi$-limits, the inclusion $\mathcal{L} \hookrightarrow \mathcal{FL}$ has a right adjoint $R$ inducing an algebraic functor $R^{\ast} \colon \Phi$-$\mathbf{Cts}(\mathcal{L},\mathcal{V}) \to \Phi$-$\mathbf{Cts}(\mathcal{FL},\mathcal{V}) \simeq [\mathcal{L},\mathcal{V}]$. But we just showed that algebraic functors have left adjoints, giving us the following theorem.

Theorem. $\Phi$-$\mathbf{Cts}(\mathcal{L},\mathcal{V})$ is reflective in $[\mathcal{L},\mathcal{V}]$.

As promised, in the two general contexts corresponding to the axioms B1 and B2, we have the Lawvere theory-monad correspondence, that algebraic functors have left adjoints, and that categories of models are reflective.

An example

After all of that abstract nonsense, let’s get our feet back on the ground. Here is an example of manifesting a category with a chosen terminal object as a generalized Lawvere theory. This comes courtesy of Nishizawa and Power.

Let $\mathbf{0}$ denote the empty category, $\mathbf{1}$ the terminal category, and $\mathbf{2}$ the category $\{a \to b\}$ with two objects and a single arrow between them. We will also take $\mathcal{K} = \mathcal{V} = \mathbf{Cat}$. The class of limits $\Phi$ here is the finite $\mathbf{Cat}$-powers. We define a Lawvere $\Phi$-theory $\mathcal{L}$ to be the $\mathbf{Cat}$-category where we formally add to $\mathbf{Cat}^{\text{op}}_{\text{fp}}$ (the opposite full subcategory on the finitely presentable objects) two arrows: $\tau \colon \mathbf{0} \to \mathbf{1}$ and $\sigma \colon \mathbf{1} \to \mathbf{2}$. We then close up under finite $\mathbf{Cat}$-powers and modulo the commutative diagrams

$\quad \quad$ $\quad \quad$

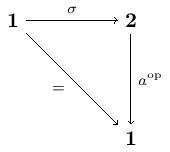
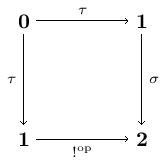
Now $\mathcal{L}$ is the Lawvere $\Phi$-theory for a category with a chosen terminal object. A model of $\mathcal{L}$ is a $\Phi$-continuous $\mathbf{Cat}$-functor $\mathcal{L} \to \mathbf{Cat}$. This means that if $M$ is a model, it must preserve powers and so the following diagrams must commute:

$\quad \quad$ $\quad \quad$

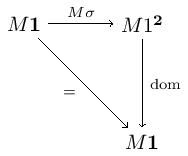
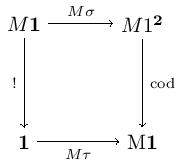
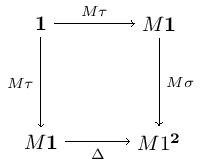
Here $\text{dom}$ and $\text{cod}$ choose the domain and codomain, and $\Delta$ the diagonal functor. Note that the commutativity of these diagrams witnesses the preservation of raising the terminal category to the first three diagrams given. Let’s parse these diagrams out.

The category we get from the model $M$ is $M1$ and the distinguished terminal object $t$ is chosen by $M\tau$. The first two diagrams provide a morphism $x \to t$ for every object $x$ in $M1$. The third diagram gives the identity map on $t$. The uniqueness of maps into $t$ follows from the functorality of $M\sigma$ and $\text{cod}$.

Conversely, given a category $\mathbf{C}$ with a chosen terminal object $t$, define a model $M \colon \mathcal{L} \to \mathbf{Cat}$ by $\mathbf{1} \to \mathbf{C}$ and $\mathbf{1}^x \to \mathbf{C}^x$ for $\mathcal{L}$-objects $x$. Also, let $M\tau$ choose $t$ and let $M \sigma$ send each $\mathcal{L}$-object $x$ to the $! \colon x \to t$.