Algebra Valued Functors in General and Tensor Products in Particular
Posted by Emily Riehl
Guest post by Maru Sarazola
The Kan Extension Seminar II continues, and this time we focus on the article “Algebra valued functors in general and tensor products in particular” by Peter Freyd, published in 1966. Its purpose is to present algebraic theories and some related notions in a way that doesn’t make use of elements, so the concepts can later be applied to any category (satisfying some restrictions).
Concerned that the language of categories was not popular enough at the time, he chooses to target a wider audience by taking an “equational” approach in his exposition (in contrast, for example, to Lawvere’s more elegant approach, purely in terms of functors and natural transformations). I must say that this perspective, which nowadays might seem somewhat cumbersome, greatly helped solidify my understanding of some of these notions and constructions.
Before we start, I would like to thank Brendan Fong, Alexander Campbell and Emily Riehl for giving me the opportunity to take part in this great learning experience, and all the other participants for their enlightening comments and discussions. I would also like to thank my advisor, Inna Zakharevich, for her helpful comments and especially for her encouragement throughout this entire process.
Algebraic theories and their algebras
An algebraic theory is a family of operator symbols , together with non-negative integers and equations relating the ’s, each of which looks in the equations as if it were a function on arguments.
For a locally small category with finite products, we say that is a -algebra if it admits a -structure, meaning each operator has an interpretation such that all equations are true when interpreted as maps in . Interpretations of these -ary expressions follow the rules:
- If , then we interpret as the -th projection.
- If and we have already interpreted the ’s as and ’s as , then we interpret as .
We will denote by the category of -algebras and homomorphisms in .
Even though Freyd’s equational approach is (purposefully) quite different, these notions are equivalent to the ones introduced by Lawvere and mentioned previously in Evangelia’s post.
Recall that a Lawvere theory is a small category with finite products, together with a strict finite-product preserving identity-on-objects functor , and a model for the theory is a finite-product preserving functor . In this case, the operators determine the non-basic operations in (i.e. maps not coming from the product structure), with the equations corresponding to composition in . As to the algebras/models, an algebra with interpretations corresponds to the finite-product preserving functor such that and .
Constants and 0’ary operations
It seems necessary to take a moment to discuss ‘ary operations, since Freyd decides to take a non-conventional approach. It is natural to think of the interpretation of ‘ary operations as constants, and so we could say that a ‘ary operation on is a constant unary operation, i.e. a map where for every and all maps and .
However, this comes with a problem: setting , the empty set would be an algebra for every algebraic theory –even those that have constants– and all our algebraic intuition revolts against this! To fix this problem, Freyd defines a generalized ‘ary operation: a collection of maps such that for every map the diagram commutes
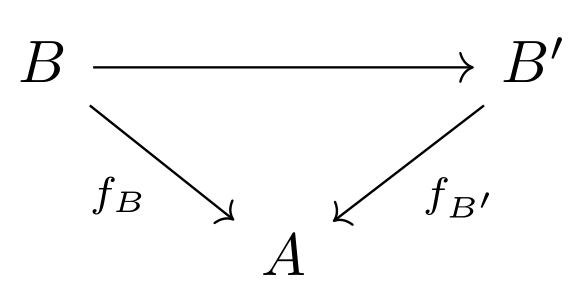
Given such a collection, it’s clear from the definition that would be a constant map; reciprocally, given a constant map, we can take that to be and then the commutative diagram ensures us that every other is automatically determined by any map . This shows that it is reasonable to consider maps as our ‘ary operations.
We must be careful though, because it might be the case that for some , which makes it impossible to build such a collection. Whenever this is the case, we will say that there are no ‘ary operations on and therefore cannot be a -algebra for any algebraic theory that has ‘ary operations.
Although this treatment of constants and ‘ary operations eliminates the problem of the empty set, it seems terribly unnatural to me. I’m left wondering, why didn’t Freyd define a ‘ary operation on as a map where is the terminal object in ? Are there important examples of categories over which we want to consider algebras for certain theories, and that don’t have a terminal object? (I don’t know of any, I’m hoping someone here will)
Co-algebras
As usual, we obtain a notion of -co-algebra by dualizing the definition of -algebra; in other words, a -co-algebra in is precisely a -algebra in . However, as we will soon see, co-algebras will not be relegated to a dualizing afterthought and will instead play a key role in the understanding of algebra valued functors.
Example. Let’s take a look at an example. Let be the algebraic theory of groups, and the category of pointed spaces and homotopy classes of maps. In this case the coproduct is the wedge of spaces, and a space is a -co-group if there exists a co-product , a co-inverse map and a co-unit satisfying diagrams dual to the group diagrams. As a concrete example we have the -spheres for , which admit a co-group structure by taking to be the operation that collapses the equator of to a point, that collapses to the basepoint, and where is any orientation-reversing map (they are all homotopic, after all!). We get the necessary commutative diagrams
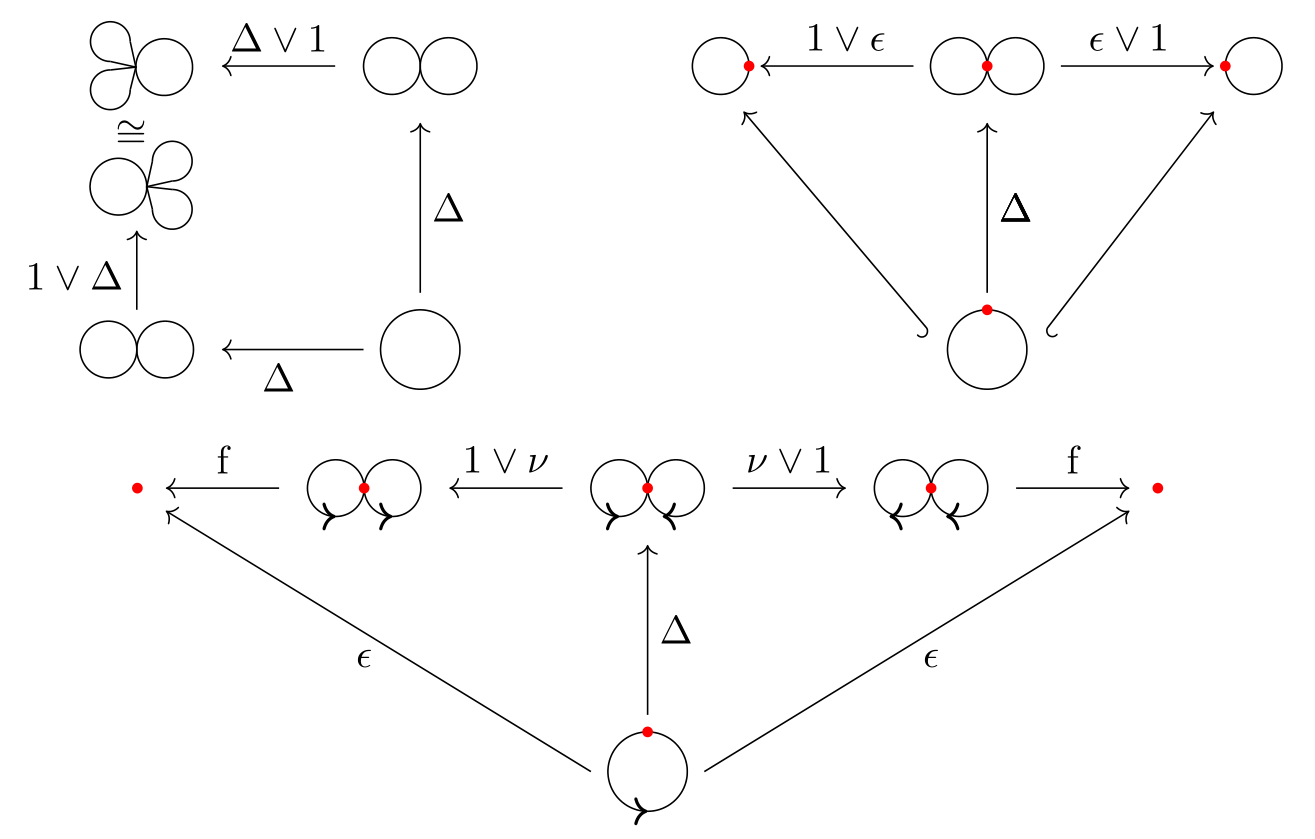
where –for “fold”– is the operation dual to the diagonal map . Note that this wouldn’t work in , since we only have co-associativity up to homotopy.
Algebra valued functors
Fix and denote by the contravariant hom-set functor. For any , we can give a -algebra structure as follows: given an operator in , and the interpretation determined by the algebra structure of , we can take its interpretation to be the composition All equations of the theory will be preserved, since is a product-preserving functor. Thus, is an algebra valued functor and we can write . Similarly, if is a -co-algebra in , the covariant functor will be algebra valued.
Example: Returning to our example of the -spheres, note that the wedge sum co-product gives a group structure for any pointed space , which is precisely the usual group structure of the homotopy groups!
Interestingly, the converse of the previous statement is also true! Algebra valued representable functors yield canonical (co)structures on their representatives, so we can actually state the following:
is a -co-algebra (resp. is a -algebra) if and only if the functor (resp. ) is algebra valued.
To show this less evident converse, fix an operator in ; using the -algebra structure of we have, for every , a map It suffices to show that these maps can be put together to form a natural transformation since then, by Yoneda, it must come from a map which we take as the co-interpretation of .
This amounts to showing that, for any , the following commutes
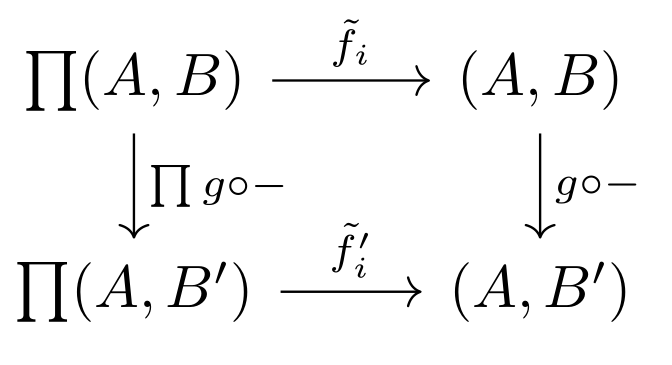
But is an algebra valued functor, so must be a homomorphism, which by definition translates into that diagram being commutative.
For the case of algebra valued functors where is complete, we have that is representable if and only if it has a left adjoint (Theorem 2 in the article). This fact, together with a translation of the general adjoint functor theorem to this algebraic context, yields for any infinite cardinal
A functor is representable by a -algebra with or less generators (and with a -co-structure) if and only if preserves products, kernel pairs, and -directed unions.
The canonical co-structure on free algebras
Let be an algebraic theory and let in be the free algebra on one generator . Then admits a canonical -co-algebra structure:
First note that is the free -algebra on generators , since “free” constructions preserve colimits. Thus, each operator in has an interpretation The canonical co-interpretation of that gives a co-algebra structure is Chasing the operations around, it’s possible to see that this is the only co-structure on (up to isomorphism) which makes naturally equivalent to the identity functor.
Tensor products of theories
For two algebraic theories and , we would like to find a theory with the property that , i.e. we want -algebras to be the objects with a -structure and a structure and such that every operation is a homomorphism. Let’s make this last condition explicit: every pair of operators , , must satisfy
It’s easy to see that the theory we are looking for has as operators the disjoint union of operators in and , and as equations all the equations found in and , along with all possible equations of the form (1). If we denote such a theory by , then the equivalence with the notion of tensor product of Lawvere theories becomes apparent, as they were both defined to satisfy the universal properties
In contrast to the tensor of Lawvere theories, this explicit formulation makes it simple to compute some basic examples. Let be the theory of modules over a ring (this has all the operators and equations found in the theory of abelian groups, with the addition of one unary operator for every that acts as “multiplication by ”, and the diagrams ensuring that these define a ring action).
- If is the theory of modules over , then -algebras on will be abelian groups that admit both and actions. Furthermore, equation (1) imposes commutativity among these actions: , and so we find that is the theory of modules over .
- If is the theory with one unary operator and no equations, then is the theory of modules over the polynomial ring .
- If is the theory with unary operators and no equations, then is the theory of modules over where the variables don’t commute (recall that equation (1) is only enforced between an operator of and one of , not among operators from the same theory).
This generalizes to the following impressive result:
If is the theory of modules over a semi-ring, then for any , there exists a semi-ring such that is the theory of modules over .
An application: theories for closed categories
A category is autonomous (according to Linton) if there exists a functor and a forgetful functor such that . If we restrict ourselves to algebraic theories such that their categories of algebras are autonomous, then these theories are also those which have their categories of algebras closed.
If is such a theory, then the fact that we can see as algebra valued means that each has a canonical -structure in . This gives us an embedding , and therefore * must be such that every operator is a homomorphism*; in other words, all operators in commute, in the sense of (1).
As an example, if is once again the theory of modules over , then the largest subtheory such that is closed will be the largest subtheory with commutative operators: the theory of modules over the center of .
Lawvere functors
A Lawvere functor is a functor that preserves underlying sets. Since trivially preserves products, kernel pairs and directed unions, it must be representable; say for some with a co-structure. Then (as sets) for every , so must be the free algebra on one generator. We see that Lawvere functors are in one-to-one correspondence with the -co-structures we can place on the free -algebra.
Now, when choosing a -co-structure for the free -algebra we get, for each operator , an interpretation . This will of course be determined by its image on the generator, , which is in turn an expression in of the same arity as . This shows that -co-structures on the free -algebra are in one-to-one correspondence with theory maps .
We have just built a contravariant functor from the category of algebraic theories to the category of categories, which is no other than Lawvere’s Semantics functor!
Some questions left unanswered
Freyd’s way of dealing with ‘ary operations has been a thorn in my side ever since reading this article. I would love to understand the reason for his choice of definitions, that seems so artificial to me.
A comment regarding ‘ary co-operations that might be of relevance: by dualizing the definitions, we obtain the notions of co-constant map and generalized ‘ary co-operation, which will be in one-to-one correspondence with each other except in the case where for some ; in this case we say that doesn’t admit a -co-algebra structure for any with ‘ary operations.
If we consider the case of the free -algebra on one generator , we see that only when . Since we are taking , that would imply that the theory has no ‘ary operations itself. This makes sense, of course, because we already know that always has a canonical co-structure.
Could the co-algebras be the reason behind these definitions? Are we interested in studying algebras over categories with terminal but no initial object, and if so, are we particularly interested in them having co-algebras too?
- Equation (1) has a taste of a really nice distributive law. Is there a relation between tensors of theories and distributive laws, perhaps asking the latter to satisfy some nice properties? A few clarifying answers have appeared among our reading responses; I look forward to seeing this discussion here!

Re: Algebra Valued Functors in General and Tensor Products in Particular
I don’t know why Freyd chose to single out 0-ary operations in that way, but there is a more abstract way to describe what he’s doing that applies also to -ary operations for all . Recall that for any locally small category , the Yoneda embedding preserves all limits that exist in , while the presheaf category is complete. Therefore, in any (locally small) category at all, we can define a -algebra in to be a -algebra in (in the naive sense) whose underlying object is representable.
If has finite products, this agrees with the more direct definition, because the Yoneda embedding preserves products. If doesn’t necessarily have a terminal object, then the 0-ary operations are interpreted as natural transformations from the terminal presheaf into , which if you unravel it is exactly a “generalized 0-ary operation”. Similarly, if lacks binary products, then the binary operations are interpreted as natural transformations , i.e. operations assigning to each pair of morphisms and another morphism , in a way that varies naturally with .
It’s also worth noting that since limits in are objectwise, a -algebra in is the same as a functor from to the category of -algebras in . Thus, to give a -algebra structure is equivalently to lift its representable functor along the forgetful functor .