On Clubs and Data-Type Constructors
Posted by Emily Riehl
Guest post by Pierre Cagne
The Kan Extension Seminar II continues with a third consecutive of Kelly, entitled On clubs and data-type constructors. It deals with the notion of club, first introduced by Kelly as an attempt to encode theories of categories with structure involving some kind of coherence issues. Astonishing enough, there is no mention of operads whatsoever in this article. (To be fair, there is a mention of “those Lawvere theories with only associativity axioms”…) Is it because the notion of club was developed in several stages at various time periods, making operads less identifiable among this work? Or does Kelly judge irrelevant the link between the two notions? I am not sure, but anyway I think it is quite interesting to read this article in the light of what we now know about operads.
Before starting with the mathematical content, I would like to thank Alexander, Brendan and Emily for organizing this online seminar. It is a great opportunity to take a deeper look at seminal papers that would have been hard to explore all by oneself. On that note, I am also very grateful for the rich discussions we have with my fellow participants.
Non symmetric Set-operads
Let us take a look at the simplest kind of operads: non symmetric -operads. Those are informally collections of operations with given arities closed under compositions. The usual way to define them is to endow the category of -indexed families of sets with the substitution monoidal product (see Simon’s post): for two such families and , This monoidal product is better understood when elements of and are thought as branching with inputs and one output: is then obtained by plugging outputs of elements of to the inputs of elements of . A non symmetric operad is defined to be a monoid for that monoidal product, a typical example being the family for a set .
We can now take advantage of the equivalence to equip the category with a monoidal product. This equivalence maps a family to the coproduct with the canonical map to , while the inverse equivalence maps a function to the family of fibers . It means that a -indexed family can be thought either as a set of operations of arity for each or as a bunch of operations, each labeled by an integer given its arity. Let us transport the monoidal product of to : given two maps and , we compute the -product of the family of fibers, and then take the coproduct to get with the map mapping . That is, the monoidal product is achieved by computing the following pullback:
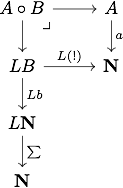
where is the free monoid monad (or list monad) on . Hence a non symmetric operad is equivalently a monoid in for this monoidal product. In Burroni’s terminology, it would be called a -category with one object.
In my opinion, Kelly’s clubs are a way to generalize this point of view to other kind of operads, replacing by the groupoid of bijections (to get symmetric operads) or the category of finite sets (to get Lawvere theories). Obviously, or does not make much sense, but the coproduct functor of earlier can be easily understood as a Grothendieck construction that adapts neatly in this context, providing functors: Of course, these functors are not equivalences anymore, but it does not prevent us from looking for monoidal products on and that restrict to the substitution product on the essential images of these functors (i.e. the discrete opfibrations). Before going to the abstract definitions, you might keep in mind the following goal: we are seeking those small categories such that admits a monoidal product reflecting through the Grothendieck construction the substition product in .
Abstract clubs
Recall that in a monoidal category with product and unit , any monoid with multiplication and unit induces a monoidal structure on as follows: the unit is and the product of by is the composite Be aware that this monoidal structure depends heavily on the monoid . For example, even if is finitely complete and is the cartesian product, the induced structure on is almost never the cartesian one. A notable fact about this structure on is that the monoids in it are exactly the morphisms of monoids with codomain .
We will use this property in the monoidal category of endofunctors on a category . I will not say a lot about size issues here, but of course we assume that there exist enough universes to make sense of as a category even when is not small but only locally small: that is, if smallness is relative to a universe , then we posit a universe big enough to contain the set of objects of , making a -small category hence a locally -small category. The monoidal product on is just the composition of endofunctors and the unit is the identity functor . The monoids in that category are precisely the monads on , and for any such with multiplication and unit , the slice category inherits a monoidal structure with unit and product the composite for any and .
Now a natural transformation between two functors is said to be cartesian whenever the naturality squares
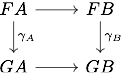
are pullback diagrams. If is finitely complete, as it will be for the rest of the post, it admits in particular a terminal object and the pasting lemma ensures that we only have to check for the pullback property of the naturality squares of the form
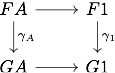
to know if is cartesian. Let us denote by the (possibly large) set of morphsisms in that are cartesian in this sense, and denote by the full subcategory of whose objects are in .
Definition. A club in is a monad such that is closed under the monoidal product .
By “closed under ”, it is understood that the unit of is in and that the product of two elements of with codomain still is in . A useful alternate characterization is the following:
Lemma. A monad is a club if and only if and .
It is clear from the definition of that the condition is sufficient, as the can be written as via the exchange rule. Now suppose is a club: as it is the monoidal unit; comes from ; finally for any , we should have , and having already this yields by the pasting lemma.
In particular, this lemma shows that monoids in , which coincide with monad maps for some monad , are clubs too. We shall denote the category of these by .
The lemma also implies that any cartesian monad, by which is meant a pullbacks preserving monad with cartesian unit and multiplication, is automatically a club.
Now note that evaluation at provides an equivalence whose pseudo inverse is given for a map by the natural transformation pointwise defined as the pullback
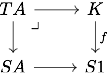
The previous monoidal product on can be transported on and bears a fairly simple description: given and , the product, still denoted , is the evaluation at of the composite where corresponds to and to . Hence the explicit equivalence given above allows us to write this as
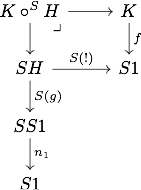
Definition. By abuse of terminology, a monoid in is said to be a club over .
Examples of clubs
On , the free monoid monad is cartesian, hence a club on in the above sense. Of course, we retrieve as the monoidal product of the introduction on . Hence, clubs over in are exactly the non symmetric -operads.
Considering as a -category, the free finite coproduct category monad on is a club in the above sense. This can be shown directly through the charaterization we stated earlier: its unit and multiplication are cartesian and it maps cartesian transformations to cartesian transformations. Moreover, the obvious monad map is cartesian, where is the free strict symmetric monoidal category monad on . Hence it yields for free that is also a club on . Note that the groupoid of bijections is and the category of finite sets is . So it is now a matter of careful bookkeeping to establish that the functors (given by the Grothendieck construction) are strong monoidal where the domain categories are given Kelly’s substition product. In other words, it exhibits symmetric -operads and non enriched Lawvere theories as special clubs over and .
We could say that we are done: we have a polished abstract notion of clubs that can encompass the different notions of operads on that we are used to. But what about operads on other categories? Also, the above monads and are actually -monads on when seen as a -category. Can we extend the notion to this enrichement?
Enriched clubs
We shall fix a cosmos to enriched over (and denote as usual the underlying ordinary notions by a -index), but we want it to have good properties, so that finite completeness makes sense in this enriched framework. Hence we ask that is locally finitely presentable as a closed category (see David’s post). Taking a look at what we did in the ordinary case, we see that it heavily relies on the possibility of defining slice categories, which is not possible in full generality. Hence we ask for to be semicartesian, meaning that the monoidal unit of is its terminal object: then for a -category , the slice category is defined to have elements as objects, and the space of morphisms between such and is given by the following pullback in :
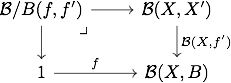
If we also want to be able to talk about the category of enriched clubs over something, we should be able to make a -category out of the monoids in a monoidal -category. Again, this is a priori not possible to do: the space of monoid maps between and is supposed to interpret “the subspace of those such that and for all ”, where the later equation has two occurences of on the right. Hence we ask that is actually a cartesian cosmos, so that the interpretation of such a subspace is the joint equalizer of
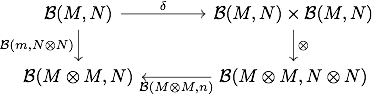
Moreover, these hypothesis also resolve the set theoretical issues: because of all the hypotheses on , the underlying identifies with the category of -valued left exact functors from the finitely presentables of . Hence, for a -category , the category of -endofunctors is naturally a -category for the cartesian cosmos where is the category of -small sets for a universe big enough to contain the set of objects of . Hence we do not care so much about size issues and consider everything to be a -category; the careful reader will replace by when necessary.
In the context of categories enriched over a locally finitely presentable cartesian closed cosmos , all we did in the ordinary case is directly enrichable. We call a -natural transformation cartesian just when it is so as a natural transformation , and denote the set of these by . For a -monad on , the category is the full subcategory of the slice spanned by the objects in .
Definition. A -club on is a -monad such that is closed under the induced -monoidal product of .
Now comes the fundamental proposition about enriched clubs:
Proposition. A -monad is a -club if and only if is an ordinary club.
In that case, the category of monoids in is composed of the clubs together with a -monad map in . We will still denote it and its underlying ordinary category is . We can once again take advantage of the -equivalence to equip the later with a -monoidal product, and abuse terminlogy to call its monoids -clubs over . Proving all that carefully require notions of enriched factorization systems that are of no use for this post.
So basically, the slogan is: as long as is a cartesian cosmos which is loccally presentable as a closed category, everything works the same way as in the ordinary case, and preserves and reflects clubs.
Examples of enriched clubs
As we said earlier, and are -monads on , and the underlying and (earlier just denoted and ) are ordinary clubs. So and are -clubs, maybe better called -clubs. Moreover, the map mentioned earlier is easily promoted to a -natural transformation making a -club over .
The free monoid monad on a cartesian cosmos is a -club and the clubs over are precisely the non symmetric -operads.
Last but not least, a quite surprising example at first sight. Any small ordinary category is naturally enriched in its category of presheaves , as the full subcategory of the cartesian cosmos spanned by the representables. Concretely, the space of morphisms between and is given by the presheaf Hence an -endofunctor on is the data of a map on objects, together with for any a -natural transformation satisfying some axioms. Now fixing , the collection of is equivalently, via Yoneda, a collection of The axioms that satisfies as a -enriched natural transformation make a strength for the endofunctor . Along this translation, a strong monad on is then just a -monad. And it is very common, when modelling side effects by monads in Computer Science, to end up with strong cartesian monads. As cartesian monads, they are in particular ordinary clubs on . Hence, those are -monads whose underlying ordinary monad is a club: that is, they are -clubs on .
In conclusion, let me point out that there is much more in Kelly’s article than presented here, especially on local factorisation systems and their link to (replete) reflexive subcategories with a left exact reflexion. It is by the way quite surprising that he does not stay in full generality longer, as one could define an abstract club in just that framework. Maybe there is just no interesting example to come up with at that level of generality…
Also, a great deal of examples of club comes from never published work of Robin Cockett (or at least, I was not able to find it), so these motivations are quite difficult to follow.
Going a little further in the generalization, the cautious reader should have noticed that we did not say anything about coloured operads. For then we would not have to look at slice categories of the form , but at categories of span with one leg pointing to (morally mapping an operation to its coloured arity) and the other one to (morally picking the output colour), where the is the object of colours. Those spans actually appear above implicitly whenever a map or the form is involved (morally, this is the map picking the “only output colour” in a non coloured operad). This somehow should be contained somewhere in Garner’s work on double clubs or in Shulman’s and Cruttwell’s unified framework for generalized multicategories. I am looking forward to learn more about that in the comments!

Re: On Clubs and Data-Type Constructors
I have a quick question about your section on enriched clubs: why do we need to be semi-cartesian in order to define the slice category? The pullback that defines doesn’t require to be terminal.
I guess we later have to require to be cartesian anyway (and I can see how we need cartesianness to get ), so it’s not really an important question.
Nice post, by the way, and thanks for highlighting the link to the substitution product for operads!