The Geometric McKay Correspondence (Part 2)
Posted by John Baez
Last time I sketched how the Dynkin diagram arises from the icosahedron. This time I’m fill in some details. I won’t fill in all the details, because I don’t know how! Working them out is the goal of this series, and I’d like to enlist your help.
As Kennedy said: ask not what your n-Café can do for you. Ask what you can do for your n-Café!
Remember the basic idea. We start with the rotational symmetry group of the isosahedron and take its double cover, getting a 120-element group called the binary icosahedral group. Since this is naturally a subgroup of it acts on , and we can form the quotient space
This is a smooth manifold except at the origin — by which I mean the point coming from . Luckily we can ‘resolve’ this singularity! This implies that we can find a smooth manifold and a smooth map
that’s one-to-one and onto except at the origin. There may be various ways to do this, but there’s one best way, the ‘minimal’ resolution, and that’s what I’ll be talking about.
The origin is where all the fun happens. The map sends 8 spheres to the origin in , one for each dot in the Dynkin diagram:
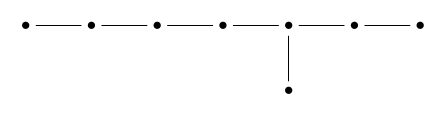
Two of these spheres intersect in a point if their dots are connected by an edge; otherwise they’re disjoint.
This is wonderful! So, the question is just how do we really see it? For starters, how do we get our hands on this manifold and this map ?
For this we need some algebraic geometry. Indeed, the whole subject of ‘resolving singularities’ is part of algebraic geometry! However, since I still remember my ignorant youth, I want to avoid flinging around the vocabulary of this subject until we actually need it. So, experts will have to pardon my baby-talk. Nonexperts can repay me in cash, chocolate, bitcoins or beer.
What’s like? First I’ll come out and tell you, and then I’ll start explaining what the heck I just said.
Theorem. is the space of all -invariant ideals such that is isomorphic, as a representation of , to the regular representation of .
If you want a proof, this is Corollary 12.8 in Kirillov’s Quiver Representations and Quiver Varieties. It’s on page 245, so you’ll need to start by reading lots of other stuff. It’s a great book! But it’s not completely self-contained: for example, right before Corollary 12.8 he brings in a crucial fact without proof: “it can be shown that in dimension 2, if a crepant resolution exists, it is minimal”.
I will not try to prove this theorem; instead I will start explaining what it means.
Suppose you have a bunch of points . We can look at all the polynomials on that vanish at these points. What is this collection of polynomials like?
Let’s use and as names for the standard coordinates on , so polynomials on are just polynomials in these variables. Let’s call the ring of all such polynomials . And let’s use to stand for the collection of such polynomials that vanish at our points .
Here are two obvious facts about :
A. If and then .
B. If and then .
We summarize these by saying is an ideal, and this is why we called it . (So clever!)
Here’s a slightly less obvious fact about :
C. If the points are all distinct, then has dimension .
The point is that the value of a function at a point doesn’t change if we add an element of to , so this value defines a linear functional on . Guys like this form a basis of linear functionals on , so it’s -dimensional.
All this should make you interested in the set of ideals with . This set is called the Hilbert scheme .
Why is it called a scheme? Well, Hilbert had a bunch of crazy schemes and this was one. Just kidding: actually Hilbert schemes were invented by Grothendieck in 1961. I don’t know why he named them after Hilbert. The kind of Hilbert scheme I’m using is a very basic one, more precisely called the ‘punctual’ Hilbert scheme.
The Hilbert scheme is a whole lot like the set of unordered -tuples of distinct points in . Indeed, we’ve seen that every such -tuple gives a point in the Hilbert scheme. But there are also other points in the Hilbert scheme! And this is where the fun starts!
Imagine particles moving in , with their motion described by polynomial functions of time. As long as these particles don’t collide, they define a curve in the Hilbert scheme. But it still works when they collide! When they collide, this curve will hit a point in the Hilbert scheme that doesn’t come from an unordered -tuple of distinct points in . This point describes a ‘type of collision’.
More precisely: -tuples of distinct points in give an open dense set in the Hilbert scheme, but there are other points in the Hilbert scheme which can be reached as limits of those in this open dense set! The topology here is very subtle, so let’s look at an example.
Let’s look at the Hilbert scheme . Given two distinct points , we get an ideal
This ideal is a point in our Hilbert scheme, since .
But there are other points in our Hilbert scheme! For example, if we take any point and any vector , there’s an ideal consisting of polynomials that vanish at and whose directional derivative in the direction also vanishes at :
It’s pretty easy to check that this is an ideal and that . We can think of this ideal as describing ‘two particles in that have collided at with relative velocity some multiple of ’.
For example you could have one particle sitting at while another particle smacks into it while moving with velocity ; as they collide the corresponding curve in the Hilbert scheme would hit .
This would also work if the velocity were any multiple of , since we also have
for any constant . And note, this constant can be complex. I’m trying to appeal to your inner physicist, but we’re really doing algebraic geometry over the complex numbers, so we can do weird stuff like multiply velocities by complex numbers.
Or, both particles could be moving and collide at while their relative velocity was some complex multiple of . As they collide, the corresponding point in the Hilbert scheme would still hit .
But here’s the cool part: such ‘2-particle collisions with specified position and relative velocity’ give all the points in the Hilbert scheme , except of course for those points coming from 2 particles with distinct positions.
What happens when we go to the next Hilbert scheme, ? This Hilbert scheme has an open dense set corresponding to triples of particles with distinct positions. It has other points coming from situations where two particles collide with some specified position and relative velocity while a third ‘bystander’ particle sits somewhere else. But it also has points coming from triple collisions. And these are more fancy! Not only velocities but accelerations play a role!
I could delve into this further, but for now I’ll just point you here:
• John Baez, The Hilbert scheme for 3 points on a surface, MathOverflow, June 7, 2017.
The main thing to keep in mind is this. As increases, there are more and more ways we can dream up ideals with . But all these ideals consist of functions that vanish at or fewer points and also obey other equations saying that various linear combinations of their first, second, and higher derivatives vanish. We can think of these ideals as ways for particles to collide, with conditions on their positions, velocities, accelerations, etc. The total number of conditions needs to be .
Now let’s revisit that description of the wonderful space we’re seeking to understand, :
Theorem. is the space of all -invariant ideals such that is isomorphic, as a representation of , to the regular representation of .
Since has 120 elements, its regular representation — the obvious representation of this group on the space of complex functions on this group — is 120-dimensional. So, points in are ideals with . So, they’re points in the Hilbert scheme .
But they’re not just any old points in this Hilbert scheme! The binary icosahedral group acts on and thus anything associated with it. In particular, it acts on the HIlbert scheme . A point in this Hilbert scheme can lie in only if it’s invariant under the action of . And given this, it’s in if and only if is isomorphic to the regular representation of .
Given all this, there’s an easy way to get your hands on a point . Just take any nonzero element of and act on it by . You’ll get 120 distinct points in — I promise. Do you see why? Then let be the set of polynomials that vanish on all these points.
If you don’t see why this works, please ask me.
In fact, we saw last time that your 120 points will be the vertices of a 600-cell centered at the origin of :
By this construction we get enough points to form an open dense subset of . These are the points that aren’t mapped to the origin by
Alas, it’s the other points in that I’m really interested in. As I hope you see, these are certain ‘limits’ of 600-cells that have ‘shrunk to the origin’… or in other words, highly symmetrical ways for 120 points in to collide at the origin, with some highly symmetrical conditions on their velocities, accelerations, etc.
That’s what I need to understand.

Re: The Geometric McKay Correspondence (Part 2)
I would guess that the Hilbert scheme (of projective space) was so named because on each connected component, the Hilbert polynomial is constant. (Hartshorne’s thesis shows a converse – the Hilbert polynomial separates the connected components.) In your examples, this polynomial is degree 0.
Probably the best way to get started on understanding the E8 Dynkin curve you’re asking about is to consider the resolution as the quiver variety of the Nakajima framing of the E8 diagram. I’m not going to give a full exegesis of Nakajima quiver varieties here so the following is only meant for pointers.
Put the 2-4-6-5-4-3-2 & 3 dimensional spaces on the E8 diagram, with maps in both directions along any edge, and put another eight 1-dimensional spaces mapping to and from those spaces.
To get the quiver variety, impose the preprojective condition along the first set of vertices (the zero level set for the complex moment map; it says that the alternating sum of all products go-out-then-back-in to a vertex v should add to 0, signs given by the original choice of orientation.)
After that you have to do a GIT quotient. If you do the stupid affine GIT quotient, then you get the C^2/Gamma singular variety. Your question is about the extra info in the more interesting quotients.
I suspect the data of a point in the singular variety is given by the maps between the 1-d spaces (go down into the original E8, wander around, come back up into another 1-d space). So I think the extra equations you want, to say (in the Hilbert scheme language) that your points are all at the origin, are that these maps between the 1-d spaces are all 0.
Let’s warm up with the C^2/Z3 case, where the quiver is A2 not E8, whose Nakajima doubling looks like 1-1-1-1. Call the maps (really just numbers) 1-a->1-b->1-c->1 and 1<-x-1<-y-1<-z-1. Then the preprojective conditions are ax = by = cz. But now I also suggest to impose abc = 0 and xyz = 0. I’m guessing that the stability conditions in the GIT quotient say that a,z are not zero, so the equations become bc = xy = 0. Now there are two components, x=b=c=0 and x=y=c=0, which is what I was hoping to get for the A2 case.