The Geometric McKay Correspondence (Part 1)
Posted by John Baez
The ‘geometric McKay correspondence’, actually discovered by Patrick du Val in 1934, is a wonderful relation between the Platonic solids and the ADE Dynkin diagrams. In particular, it sets up a connection between two of my favorite things, the icosahedron:

and the Dynkin diagram:
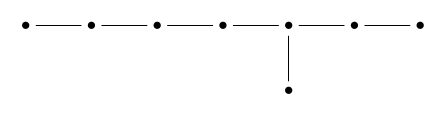
When I recently gave a talk on this topic, I realized I didn’t understand it as well as I’d like. Since then I’ve been making progress with the help of this book:
- Alexander Kirillov Jr., Quiver Representations and Quiver Varieties, AMS, Providence, Rhode Island, 2016.
I now think I glimpse a way forward to a very concrete and vivid understanding of the relation between the icosahedron and E8. It’s really just a matter of taking the ideas in this book and working them out concretely in this case. But it takes some thought, at least for me. I’d like to enlist your help.
The rotational symmetry group of the icosahedron is a subgroup of with 60 elements, so its double cover up in has 120. This double cover is called the binary icosahedral group, but I’ll call it for short.
This group is the star of the show, the link between the icosahedron and E8. To visualize this group, it’s good to think of as the unit quaternions. This lets us think of the elements of as 120 points in the unit sphere in 4 dimensions. They are in fact the vertices of a 4-dimensional regular polytope, which looks like this:
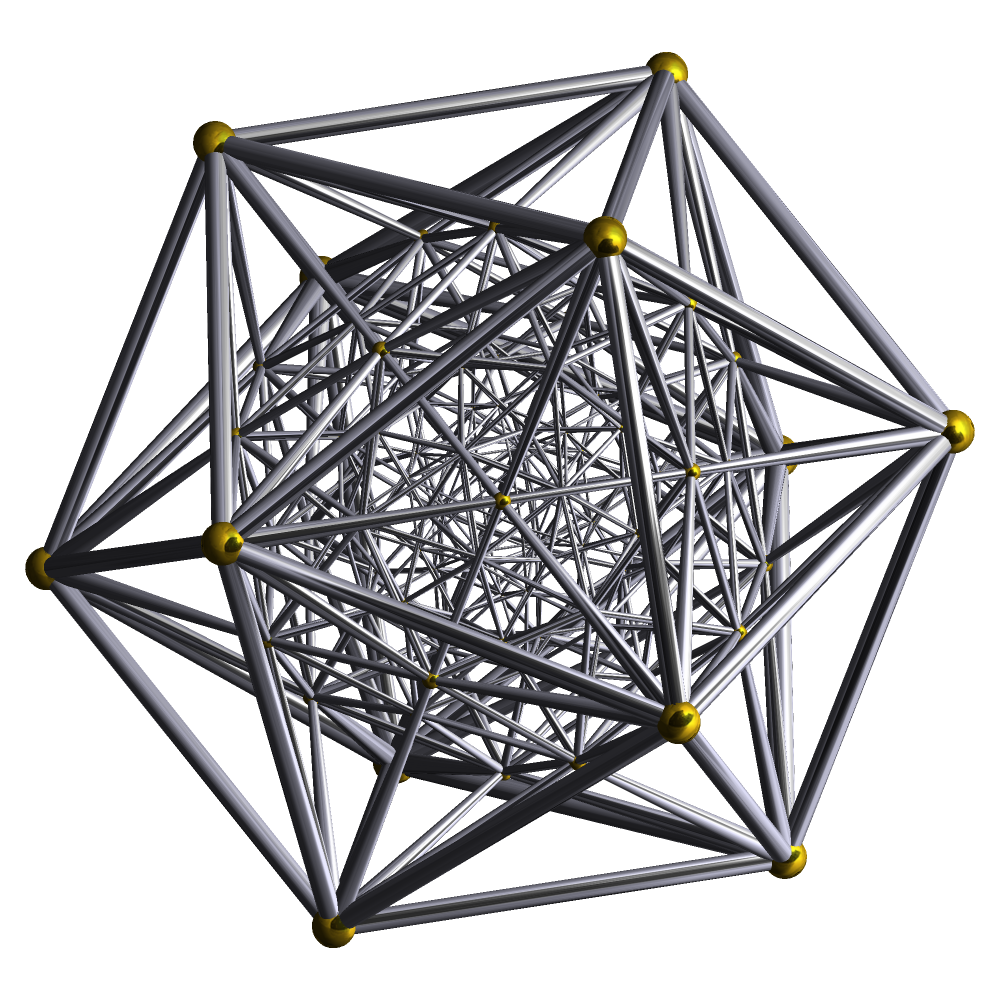
It’s called the 600-cell.
Since is a subgroup of it acts on , and we can form the quotient space
This is a smooth manifold except at the origin—that is, the point coming from . There’s a singularity at the origin, and this where is hiding! The reason is that there’s a smooth manifold and a map
that’s one-to-one and onto except at the origin. It maps 8 spheres to the origin! There’s one of these spheres for each dot here:

Two of these spheres intersect in a point if their dots are connected by an edge; otherwise they’re disjoint.
The challenge is to find a nice concrete description of , the map , and these 8 spheres.
But first it’s good to get a mental image of . Each point in this space is a orbit in , meaning a set like this:
for some . For this set is a single point, and that’s what I’ve been calling the ‘origin’. In all other cases it’s 120 points, the vertices of a 600-cell in . This 600-cell is centered at the point , but it can be big or small, depending on the magnitude of .
So, as we take a journey starting at the origin in , we see a point explode into a 600-cell, which grows and perhaps also rotates as we go. The origin, the singularity in , is a bit like the Big Bang.
Unfortunately not every 600-cell centered at the origin is of the form I’ve shown:
It’s easiest to see this by thinking of points in 4d space as quaternions rather than elements of . Then the points are unit quaternions forming the vertices of a 600-cell, and multiplying on the right by dilates this 600-cell and also rotates it… but we don’t get arbitrary rotations this way. To get an arbitrarily rotated 600-cell we’d have to use both a left and right multiplication, and consider
for a pair of quaternions .
Luckily, there’s a simpler picture of the space . It’s the space of all regular icosahedra centered at the origin in 3d space!
To see this, we start by switching to the quaternion description, which says
Specifying a point amounts to specifying the magnitude together with , which is a unit quaternion, or equivalently an element of . So, specifying a point in
amounts to specifying the magnitude together with a point in . But modulo the binary icosahedral group is the same as modulo the icosahedral group (the rotational symmetry group of an icosahedron). Furthermore, modulo the icosahedral group is just the space of unit-sized icosahedra centered at the origin of .
So, specifying a point
amounts to specifying a nonnegative number together with a unit-sized icosahedron centered at the origin of . But this is the same as specifying an icosahedron of arbitrary size centered at the origin of . There’s just one subtlety: we allow the size of this icosahedron to be zero, but then the way it’s rotated no longer matters.
So, is the space of icosahedra centered at the origin, with the ‘icosahedron of zero size’ being a singularity in this space. When we pass to the smooth manifold , we replace this singularity with 8 spheres, intersecting in a pattern described by the Dynkin diagram.
Points on these spheres are limiting cases of icosahedra centered at the origin. We can approach these points by letting an icosahedron centered at the origin shrink to zero size in a clever way, perhaps spinning about wildly as it does.
I don’t understand this last paragraph nearly as well as I’d like! I’m quite sure it’s true, and I know a lot of relevant information, but I don’t see it. There should be a vivid picture of how this works, not just an abstract argument. Next time I’ll start trying to assemble the material that I think needs to go into building this vivid picture.

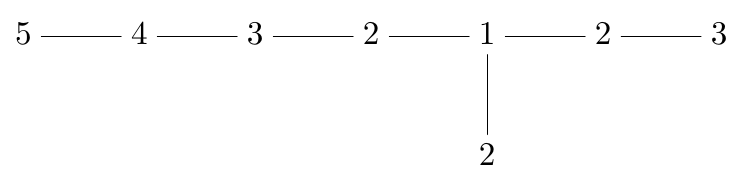
Re: The Geometric McKay Correspondence (Part 1)
From what I understand, not being an algebraic geometer, resolutions of singularities of surfaces aren’t necessarily unique, although there should be a unique minimal resolution. Is the 8-linked-spheres one you mentioned the minimal resolution? I would assume so, since it’s part of a more general construction, but am not sure. How does this look for E7?