More on Tangent Categories

August 21, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

I am the luckiest man in the world, having John Baez around here at ESI in Vienna to talk to – over breakfast, over lunch, and in between – about $n$ -curvature and that stuf which I like to think of as tangent categories and arrow-theoretic differential theory.

At the same time, the dg-wizards like Dmitry Roytenberg are around, and using that bridge which connects $n$ -categorical algebra with physicist’s BRST-BV formalism I can connect these two huge reservoirs of ideas and let the information flow botrh ways. That helps a lot.

Here are some insights which I gained by

a) trying to address questions John urged me to answer more properly, and by all the input I get from him;

b) comparing this to what the dg-BV people are doing by passing back and forth over that bridge.

More concretely, I shall

A) point out in detail how the notion of forming the “tangent category” which I was talking about coincides, in the appropriate sense and in the applicable cases, exactly with what people do who form the shifted tangent bundle of a differential graded manifold, thereby giving yet another way of making the relation of tangent categories to the ordinary notion of tangent spaces manifest.

B) indicate how one should correctly think of the $n$ -category of curvature $(n + 1)$ -functors and how this relates to the fact that they are related to universal $n$ -bundles.

C) remark on the relation of tangent categories with the Yoneda embedding

$MathML-enabled post (click for more details).$

Inner Derivations and the Shifted Tangent Bundle

Proposition Forming the Lie $(n + 1)$ -algebroid $inn (g_{(n)})$ of inner derivations a Lie $n$ -algebroid $g_{(n)}$ is equivalent to forming the the shifted tangent bundle $T [1] X_{g_{(n)}}$ of the differential graded manifold $X_{g_{(n)}}$ corresponding to $g_{(n)}$ under the duality between Lie $n$ -algebroids and dG manifolds .

Proof. It is clear that in both cases the new complex is the direct sum of the fomer one with a shifted copy of itself. The only thing to check then is if the differential that people think the shifted tangent bundle $T [1] X$ to come equipped with, for $X$ any differential graded manifold, coincides with the one demanded by the $inn (construction)$ . The latter is defined (section 3.2.5 of this provisional article) to simply be the mapping cone of the identity on the original complex.

Compare this to how the differential on $T [1] X$ is declared (which is apparently nowhere to be found fully explicitly in the literature (?), but which is exactly what I’d expect it is, and Dmitry Roytenberg kindly confirmed this to me a few minutes ago):

With $\land^{•} (V^{*}, δ)$ the original complex (locally, if we have a dG-manifold which is not a point), we form the new complex $\land^{•} (V^{*} \oplus s V^{*}, d' : = d + L_{δ}),$ where $s$ denotes the shift in degree, where we write $d t$ for the image under this shift of any element $t \in V^{*}$ (this is what is called $σ$ in our notes), where we think of $d$ as a derivation on the new complex acting as (obviously) $d : t \mapsto d t$ $d : d t \mapsto 0$ for all $t \in V^{*}$ , and where - and that’s finally the crucial point, where $L_{δ}$ acts as the original $δ$ on $V^{*}$ and anti-commutes with $d$ : $L_{δ} : t \mapsto δ t$ $L_{δ} : d t \mapsto - d (δ t) .$ Just stare at this for a second, noticing, if it helps, that what is called $d$ here is called $σ$ there and that what is called $δ$ here is called $d$ there and what is called $d + L_{δ}$ here is called $d'$ there, to see that this exactly coincides with the definition of the differential on the inner derivations. And recall, once more, that both constructions are nothing but that of forming the mapping cone

Remark Let me emphasize what this means:

I’ll concentrate on the case where we are dealing with one-object $n$ -groupoids and hence their corresponding $n$ -algebroids “over a point”, in order not to get distracted by important but boring technical issues irrelevant to the main point.

So, I said in arrow-theoretic differential theory that there is a natural notion of tangent $n$ -groupoid $T G \to G$ for any $n$ -group $G$ . In the case where $G$ has just a single object this is just the tangent groupoid $T_{•} G$ over that point. This inherits the structure of an $(n + 1)$ -group by a canonical embedding $T_{•} G ↪ T_{{Id}_{G}} (Aut (G))$ and equipped with this $(n + 1)$ -group structure I address $T_{•} G$ as (a slightly smaller sub-thing of) the inner automorphism $(n + 1)$ -group ${INN}_{0} (G) ↪ INN (G) .$ I emphasized a lot how vector fields on (the space of objects of) a category $C$ correspond to group homomorphisms into $INN (C)$ . In particular, if we are looking at smooth group homomorphisms from the additive group of real numbers, we find “ordinary” vector fields (and their orbifold-like generalizations, in fact). But this means that vector fields on the $n$ -groupoid $G$ form the Lie $n$ -algabra $inn (g) : = inn (Lie (G)) : = Lie ({INN}_{0} (G))$ of the tangent $n$ -groupoid of $G$ .

And the above proposition tells us that this notion of tangent space of an $n$ -groupoid is perfectly consistent with the notion of (shifted) tangent spaces to the corresponding dual incarnations of the corresponding Lie $n$ -algebroids.

more on $n$ -Curvature

I am claiming that for $F : C \to D$ any $n$ -functor, it makes good sense to regard its differential (section 3.2) $δ F : C \to n Cat$ which sends each object $x$ in $C$ to the tangent category $T_{F (x)} D$ , as its curvature.

Now, each $T_{F (x)} D$ is (that’s one of the crucial properties of tangent categories) “contractible” in that it is (not equal to but) equivalent to the trivial $n$ -category.

I had some kind of operational idea what this means, and that it makes good sense, but John very much urged me to come up with a good non-evil (i.e. intrinsic) statement which clarifies in one sentence what is going on, what this contractibility means and why we aren’t simply talking about the trivial $(n + 1)$ -functor, up to equivalence.

There is now some progress in this direction.

The right way to think of it is this:

Observation. For $F : C \to D$ any $n$ -functor, its differential $δ F : C \to n Cat$ really takes values in $n$ -categories over $D$ , hence $δ F : C \to n Cat ↓ D$ and hence we regard it accordingly as an object in $Hom (C, Cat ↓ D$ .

As such, it is not trivial. In fact, I think we’ll get a canonical equivalence between $n$ -functors with values in $D$ and their coresponding curvatures.

Here is a good and useful way to think about this in the special case which we are mostly interested in, that where $D = Σ G_{(n)}$ is a one-object $n$ -groupoid (set $n = 1$ or $n = 2$ to get something we understand already in detail). Then the curvature $(n + 1)$ -functor factors through $Σ INN (G_{(n)})$ , so it is helpful to think of it as $δ F : C \to Σ INN (G_{(n)}) .$ Now recall that $INN (G_{(n)})$ “is” the universal $G_{(n)}$ -bundle in that we have an exact sequence $G_{(n)} \to INN (G_{(n)}) \to Σ G_{(n)} .$ This essentially says that $INN (G_{(n)})$ is made of two copies of $G_{(n)}$ , one of them “shifted”. In fact, $INN (G_{(n)})$ is the “mapping cone of the identity on $G_{(n)}$ ”.

It is the “shifted copy” $Σ G_{(n)}$ of $G_{(n)}$ in $INN (G_{(n)})$ which hosts the various components of the curvature of $F$ . Hence if we want the transformations of $δ F$ to be those which correspond to transformations of the original $F$ , we should demand that they have no component as we pass them along the projection $INN (G_{(n)}) \to Σ G_{(n)}$ .

More formally, we take the admissable transformations of $δ F$ , which are themselves $k$ -functors with values in $Cylinders (INN (G_{(n)}))$ to become trivial as we postcompose them with $Cylinders (INN (G_{(n)})) \to Cylinder (Σ G_{(n)}) .$

This is the fancy “nonabelian” version of a rather obvious and simple statement at the level of the corresponding Lie $n$ -algebras.

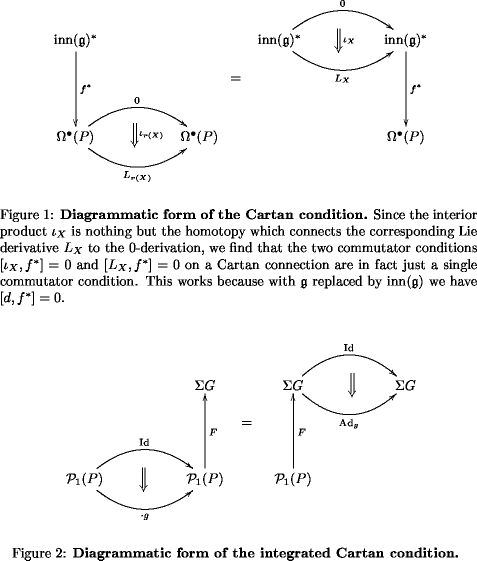
There, an $n$ -connection is a morphism $Ω^{•} (X) \leftarrow (inn (g_{(n)}))^{*}$ of the differential algebra duals of the corresponding Lie $n$ -algebras. Here the graded commutative algebra underlying $(inn (g_{(n)}))^{*}$ is $\land^{•} (s g_{(n)}^{*} \oplus s s g_{(n)}^{*})$ and our exact sequence $G_{(n)} \to INN (G_{(n)}) \to Σ G_{(n)}$ translates into the corresponding exact sequence $\land^{•} (s g_{(n)}^{*}) \leftarrow \land^{•} (s g_{(n)}^{*} \oplus s s g_{(n)}^{*}) \leftarrow \land^{•} (s s g_{(n)}^{*}) .$

Our above restriction that the morphisms between our $n$ -connection should be “projected out” by the map $INN (G_{(n)}) \to Σ G_{(n)}$ then translates into the requirement that any homotopy $Ω^{•} (X) \leftarrow (inn (g_{(n)}))^{*}$ vanishes when precomposed with the injection $\land^{•} (s g_{(n)}^{*} \oplus s s g_{(n)}^{*}) \leftarrow \land^{•} (s s g_{(n)}^{*}) .$ This is exactly what we use (without quite saying it in such a general way) in The second edge of the cube. So, for instance, the Cartan condition on an ordinary connection involves a homotopy of morphisms involving $inn (g)$ , which is precisely restricted to have no component in the “shifted part” of $inn (g)$ :

“tangential” Yoneda

When I wrote up some of the things in Arrow-theoretic differential theory, I called the corresponding pdf file tanyon.pdf. The reason is that I noticed a curious similarity of the notion of “tangent category” which I felt the need to consider, and the ordinary Yoneda embedding: the tangent category is something like a “tangential Yoneda embedding”.

But I didn’t quite know what to make of this, then. So I never mentioned it except for this hint in the title.

But now John said I might want to emphasize this point, since it might help people better follow what I am trying to talk about.

So here it is:

For any $n$ -category $C$ and any object $x \in C$ , I write $T_{x} C$ for the n-category (Yoneda would just have an $(n - 1)$ -category here!) whose objects are morphisms in $C$ emanating at $x$ , and whose morphisms are (higher dimensional) triangles between these.

(I give what I think is a very nicely abstract precise deifnition of what exactly $T_{x} C$ looks like in my notes.)

While over objects this is slightly different from standard Yoneda, morphisms and higher morphisms in $C$ give morphisms and higher morphismsm between the tangent categories $T_{x} C$ in just the same kind of way as in ordinary Yoneda embedding, such that we obtain an $n$ -functor $T C : C^{op} \to n Cat .$

Notice that the whole point of this, in a way, is that $T C$ is not an equivalent way to think of $C$ . Rather, it is a puffed-up way to think of just the space $Obj (C)$ of its objects!

That, and how, $T C$ is still something of interest is in part what my remark in the previous section was about.

Posted at August 21, 2007 9:48 AM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1397

89 Comments & 9 Trackbacks

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

I can take over while Urs is at that talk.

I’ve been struggling to understand what he’s been up to for the last few months — don’t be fooled into thinking I’ve understood all his recent blog entries! — and I feel I’m making progress.

As usual, understanding something difficult requires reworking it: making it mesh with the ideas one already knows and loves. So, let me say a word about tangent categories and the Yoneda embedding, which might help people like me understand what Urs is up to.

(“People like me” — e.g., me, but maybe other people who like the Yoneda embedding.)

Let’s take a very basic version of Urs’ tangent category construction, where it must already be familiar to category theorists.

In its crudest form — a form so contemptibly crude I’ve never even seen it mentioned — the Yoneda functor of a category $X$

$Y : X \to Set$

assigns to each object $x \in X$ the set of all arrows going into $x$ — that is, morphisms like this:

$f : y \to x .$

(To placate Bertrand Russell’s ghost, assume $X$ is small enough so that these arrows form a set instead of a proper class!)

Now, this should remind you of the tangent bundle of a manifold, which assigns to each point a set of arrows going out of that point — namely, tangent vectors!

Of course, one difference is that the arrows in the category case are not particularly ‘infinitesimal’. But we can live with that.

Another is that in the category case, the arrows are pointing into $x$ instead of out of it. We can fix that. Just consider the set of arrows going out:

$f : x \to y .$

Now we get a different sort of Yoneda functor, which is contravariant. It’s not better; it’s not worse; it’s just different. But since Urs like this one, let’s switch to working with this one:

$Y : X^{op} \to Set$

and forget about the first one I mentioned.

Now, the mere set of arrows out of $x \in X$ is a big disorganized mess. So, what most category theorists do is gather these arrows in bunches, according to where they land!

Then we get, not a mere set of arrows, but an $X$ -indexed set:

$Y : X^{op} \to {Set}^{X} .$

This is the usual Yoneda embedding — or more precisely a backwards version of it, since most category theorists focus on arrows shooting into $x \in X$ , not shooting out of it. That’s just a convention; I’ll do things the other way to please Urs, who apparently prefers to shoot arrows than to get shot by them.

But here’s the real point: Urs organizes his arrows in a somewhat different way. He organizes the arrows going out of $x \in X$ into a category! Given two arrows

$f_{1} : x \to y_{1}$

and

$f_{2} : x \to y_{2}$

he says a morphism from $f_{1}$ to $f_{2}$ is a guy

$g : y_{1} \to y_{2}$

making the obvious triangle commute. I won’t draw the triangle here, but it just says that $f_{2}$ is $f_{1}$ followed by $g$ .

So, Urs gets a souped-up Yoneda functor, which I’ll call

$T : X^{op} \to Cat .$

If one wanted, one could call this the ‘tangent category’ of $X$ . Of course, you certainly might object to that terminology! After all, it seems a bit odd to use ‘tangent category’ as the name for a functor. But, it’s no worse than thinking of the tangent bundle of a manifold $X$ as a function

$T : X \to Vect$

that assigns a vector space $T_{x}$ to each $x$ point in the manifold.

This sort of function is sometimes called a ‘classifying map’, and we can recover the total space of tangent bundle from that: a big fat space $T X$ that’s just the union of all the spaces $T_{x}$ , cleverly glued together with a nice topology. And, this total space comes with an obvious projection map

$p : T X \to X$

sending everybody in $T_{x}$ to the point $x$ .

Indeed, we can categorify this idea! We can build a ‘total category’ from Urs’ souped-up Yoneda functor

$T : X^{op} \to Cat$

in more or less the same way. Grothendieck was the guy who first thought about this sort of stuff… and if I’m not getting too confused and tripping over myself (I have a feeling I am), this ‘total category’ $T X$ will be just the ‘category of arrows in $X$ ’, equipped with a functor

$p : T X \to X$

assigning to each arrow its target, and another

$q : T X \to X^{op}$

assigning to each arrow its source.

Note, this is where the non-infinitesimal nature of our arrows really matters! A tangent vector is an arrow so short that its tip and tail lie at the same point, so we don’t get two different projections in the tangent bundle. But now, in the categorified case, we do!

Anyway, this is just a smidgen of what Urs is doing — he’s been generalizing this idea in various different directions, especially to Lie $n$ -groupoids and Lie $n$ -algebroids and the like, and using it to understand higher gauge theory and stuff like that.

But, there seems to be some simple stuff at the beginning here, which surely must have been studied before. Does anyone have thoughts about it?

Posted by: John Baez on August 21, 2007 1:32 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Thanks for this comment. I’ll have to run to get something to eat before the next talk starts, but here is a quick remark:

it is pretty important, I think, that the projection $T X \to X$ which you mention, with $X$ any $n$ -category, has $Mor (X)$ – regarded as an $n$ -category with only identity $n$ -morphisms, as its kernel, i.e. this $Mor (X) \to T X \to X$ is an “exact” sequence!

That may look like a trivial statement, but notice that when we take $X$ to be a one-object $n$ -groupoid, $X : = Σ G_{n}$ , then this sequence reads $G_{(n)} \to G_{(n)} / / G_{(n)} \to Σ G_{(n)}$ and “is” the universal $G_{(n)}$ -bundle. This vividly shows that something quite interesting is going on with these tangent $n$ -categories.

Posted by: Urs Schreiber on August 21, 2007 1:53 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

The ‘contemptibly crude’ Yoneda functor that John starts with, $Y : X \to Set$ sending $x \in X$ to ${arrows into x}$ , is usually called the Cayley embedding of the category $X$ . As the name suggests, it’s full and faithful (and injective on objects, if you care, which you probably shouldn’t). A corollary of this is that any small category $X$ is equivalent to a subcategory of Set.

In particular, if you do this for a group $X$ (viewed as a one-object category) then you get Cayley’s result that every group is a subgroup of a permutation group.

In the ‘total category’ stuff towards the end of the post, John wonders whether he’s tripping over himself. No, it looks right to me, except that I haven’t checked all the “op”s. It’s a standard example of a $Cat$ -valued functor and its corresponding fibration.

Posted by: Tom Leinster on August 21, 2007 3:28 PM | Permalink | Reply to this

Re: More on Tangent Categories

Looks like I may soon get some answers to questions I posed on the way to a (sadly neglected) categorified wreath product.

Posted by: David Corfield on August 21, 2007 3:43 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

It’s a standard example […]

Do you have a reference where this standard example is considered? Maybe also for higher $n$ ?

Posted by: Urs Schreiber on August 21, 2007 3:52 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

First of all, oops: I mis-stated the properties of the Cayley embedding. It’s faithful and injective on objects, but not usually full. Nevertheless, the conclusion stands: every small category is equivalent (in fact, isomorphic) to a subcategory of $Set$ .

I can’t name you a reference off the top of my head, but if I was looking for it I’d try looking in introductory texts on fibrations. There’s one online by Thomas Streicher, and there’s also the Handbook of Categorical Algebra by Borceux.

The only people I know who’ve written about higher-dimensional Cayley embeddings are Robin Houston and myself. (Of course, lots of people have thought about higher-dimensional Yoneda embedddings, which are very closely related.) My contribution is in Chapter III of this paper. However, this contains some mistakes, as pointed out by Robin Houston, who has further interesting thoughts.

Posted by: Tom Leinster on August 21, 2007 5:57 PM | Permalink | Reply to this

Re: More on Tangent Categories

Tom wrote:

In the “total category” stuff towards the end of the post, John wonders whether he’s tripping over himself. No, it looks right to me, except that I haven’t checked all the “op”s.

Good. I was afraid I was “tripping op” in some manner that couldn’t be fixed by merely sticking in or removing an “op” here and there.

Posted by: John Baez on August 22, 2007 12:31 PM | Permalink | Reply to this

Re: More on Tangent Categories

I haven’t quite followed the details so can’t say anything useful, but since you’re asking I think for similar-sounding constructions I was wondering about the relation between what you discuss and derived loop spaces. The reason I mention this is that the derived loop space of a variety is exactly the shifted tangent bundle T[-1] which (up to grading conventions) appears above, but the definition of a derived loop space sounds very close to what you discuss (except of course we have arrows going out of and then back into x). Also distributions on the derived loop space are Hochschild cochains of functions on the space, which are a BV algebra (or homotopical version thereof). The derived loops into BG (for a group G) are the stack G/G (nothing funny derived there). For a general stack the derived loop space is a combination of the shifted tangent complex and of the inertia, both things that seem to play a role in the world of these posts.. (I learned about this stuff from Toen’s great survey article, and it’s also explained here.)

One thing I find unsatisfying with the BV quantization story of AKSZ etc is that, if I understand correctly, by considering only dg manifolds you don’t really get gauge theories. e.g. the AKSZ Chern-Simonsy model, based on the BV algebras Urs described, doesn’t see “large” gauge transformations, only the Lie algebra (again I may have totally missed the point). That’s one reason I prefer to work with DG (or derived) stacks, which have both dg directions and automorphisms of objects. The problem is I think the difference between stable and unstable homotopical things — stably both positive and negative directions, simplicial and cosimplicial, dg and stacky, etc all meld together into one happy continuum, but for applications in TFT I think we need not dg manifolds but dg stacks.. aaaanyway.

Posted by: David Ben-Zvi on August 21, 2007 4:17 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

The derived loops into $B G$ (for a group $G$ ) are the stack $G / G$

Thanks for saying this! This seems to be the kind of statement I was looking for when we talked about this last time, though then I had not emphasized the shift sufficiently, I guess.

So, what you just said, clearly is, when passing from stacks to the groupoids presenting them, just the statement I had emphasized so much: $T Σ G = G / / G$ in my funny notation.

In words: the category whose objects are the morphisms starting at the single point of $Σ G$ (and hence, necessarily, also ending there) and whose morphisms are commuting triangles of these is nothing but the action groupoid of $G$ acting on itself from one side.

So, possibly then, it might be useful to think of “derived path spaces” here, more generally. Is anything like that considered anywhere?

One thing I find unsatisfying with the BV quantization story of AKSZ etc is that, if I understand correctly, by considering only dg manifolds you don’t really get gauge theories. e.g. the AKSZ Chern-Simonsy model, based on the BV algebras Urs described, doesn’t see “large” gauge transformations

Yes, exactly. That’s why I would like to identify the right “structure Lie $n$ -algebra” which appears here and then pass to the Lie $n$ -group integrating it.

In fact, I think this comment applies to the entire BV approach (but I might be missing something): by its very construction (as far as I perceive it) it is based on passing from the Lie $n$ -groupoid of physical configurations to just the underlying Lie $n$ -algebroid.

So, can you point me to anything like a “large” discussion of Chern-Simons using those stacky dg methods you mention?

Posted by: Urs Schreiber on August 21, 2007 4:43 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

One thing I find unsatisfying with the BV quantization story […]

That’s why I would like to identify the right “structure Lie n-algebra” which appears here and then pass to the Lie $n$ -group integrating it.

By the way, this really strikes a nerve:

after my talk I was asked:

“Why on earth do you want to understand a 3-functor underlying Chern-Simons?”

and

“Why on earth do you want to determnine a 3-group underlying Chern-Simons?”

I did try to explain why. But independent of how well I did, I found it remarkable that in the other talks in the conference one could and can see people struggling with pretty much exactly these issues – just without addressing them as such.

For instance Alberto Cattaneo a few hours ago talked about how to quantize certain Courant-algebroid sigma models on manifolds with boundary using AKSZ-BV. He described how he was trying to assign amplitudes of sorts to little squares of surfaces, trying to get a double groupoid. But, lo and behold, he finds that composition in the double groupoid works only up to certain homotopies, unless one tries to fake it.

In other words, he is seeing the need for a 3-functor! But doesn’t say so.

Posted by: Urs Schreiber on August 21, 2007 5:03 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

David, I’m a little confused, but do have a head-cold and haven’t thought about $T [- 1]$ for a while. You say that $T [- 1]$ is the derived loop space – is that what you mean? I was thinking that $O_{Δ} \otimes O_{Δ}$ (as on object in the derived category $D (X \times X)$ ) was something like functions on the derived loop space and that it is dual to the internal hom $Hom (O_{Δ}, O_{Δ})$ which when pushed down to $D (X)$ is the universal enveloping algebra of the Lie algebra $T [- 1]$ . In what (intuitive?) sense is $T [- 1]$ the derived loop space?

Posted by: Simon Willerton on August 22, 2007 12:06 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Simon, Yes that’s right, this is part of the same story about the Atiyah class etc that you explain (and apply) beautifully with Roberts. The derived loop space of a smooth variety is Spec of the Hochschild chain complex, i.e. $O_{Δ} \otimes O_{Δ}$ , which is calculated by the Koszul resolution to be the symmetric algebra of $T^{*} [1]$ , i.e. the total space of $T [- 1]$ . (The same is true in a singular setting if we take the tangent complex instead.) The derived loop space is a (homotopical version of a) bundle of groups over the base, and its Lie algebra is $T [- 1]$ (considered as a Lie algebroid or $L_{∞}$ algebroid), its enveloping algebra is the Hochschild cochains (which are distributions on the derived loop space), etc. (We explain a little of this in our paper, but didn’t give a derived loop space interpretation of the full Markarian-type story, though I think that’s a natural context for it..)

The way I see it it’s confusing to restrict to smooth schemes, because linear and nonlinear things get mixed up. If we work with stacks we see some things more clearly: if we look at BG, then $T [- 1]$ is just the Lie algebra $g$ with its adjoint action of G, but the derived loop space is $G / G$ , the adjoint quotient - $T [- 1]$ is just its linearization. Also in this setting one needs to distinguish big and small loops – ie the enveloping algebra construction really sees the formal group of the loop space, not the big loops.

That relates to my comment to Urs about Chern-Simons, which really needs the full loop space. It also relates to the question Urs is asking about negative vs positive cohomological directions – ie the stacky vs the dg directions.

Actually one gets a topological field theory out of the derived loop space which looks like a categorified form of string topology, I’m sorting out the details now with Nadler and John Francis.

Posted by: David Ben-Zvi on August 22, 2007 3:12 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

David B-Z(*),

Ah, you say $T [- 1]$ is the Lie algebra of the loop space, that’s what I was trying to get at; it’s more an infinitesimal version of the loop space (not that I really understand what that means).

What Justin Roberts and I were doing was precisely trying to mimic (perturbative) Chern-Simons theory in this context, formally using $T [- 1]$ as the Lie algebra of the gauge group and the derived category $D (X)$ as its representation category. Of course, what we wanted to say was that in the case that $X$ is symplectic there is an extended 3d TQFT with $D (X)$ as the category associated to the circle. However, at the time we (or at least I) couldn’t see how to associate this functorially to a circle – what have $D (X)$ and $T [- 1]$ got to do with maps of a circle to $X$ ?

As you say, it is instructive to consider more stacky things, and at the opposite end of the spectrum to smooth spaces you have the example of a finite group over a point (corresponding to Dijkgraaf-Witten theory). From this perspective there is the same simple, lovely, monadic categorical reason for why the group algebra of finite group (with the adjoint action) is a Hopf algebra in the category of representations and for why $π_{*} Ext (O_{Δ}, O_{Δ})$ , the universal enveloping algebra of $T [- 1]$ , is a Hopf algebra in $D (X)$ .

(*) We have three Davids on this thread – can we disambiguate (as Wikipedia would have us say) by trying some other forms of David? Anyone of you prefer Dave or Davey or Davie or Dai…?

Posted by: Simon Willerton on August 30, 2007 12:32 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Re: *, I’m happy to go as BZ for disambiguation purposes (and to save me from being called Davey..)

Simon: I agree in general for a stack T[-1] is the Lie algebra of the derived loop space - my point was that in the case of a scheme it actually is the loop space, in the sense that when we consider T[-1] as a (derived) space rather than as a vector bundle (complex) (i.e. pass to its “total space”) we get the loop space. More precisely, we know that given a vector bundle on a variety we can construct a variety mapping affinely to the original (namely the total space) by taking Spec of the symmetric algebra of the dual. In the case of T[-1], Spec of Sym T^*[1] is precisely Spec of the Hochschild homology, which is the derived loop space. Here this is just an odd nilpotent space, but it still has the formal structure of a loop space (and things like string topology operations). This is one advantage of the world of derived schemes, that such a space (Spec of a negatively graded dga for example) makes sense.

I guess the issue is the same when we consider $R^{0 ∣ 1}$ as a Lie algebra or as a group. Once you have stackiness then the shifted tangent and the derived loop space differ since the loop space gets honest points not just (odd) infinitesimals.

Is there a sequel in the works for your very enlightening paper with Justin Roberts? (I realized Roberts needs disambiguation here too..)

Posted by: David Ben-Zvi on August 30, 2007 2:52 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

David BZ,

Thanks, whilst I’m not completely on top of derived geometry [understatement], what you’re saying certainly seems to make sense.

Re a sequel: there was supposed to be a sequence of three papers. The second paper involved perturbative calculations for the TQFT, calculating S-matrices and lots of fun stuff; the third paper was on the full TQFT, and we’d done some bits and pieces with Justin Sawon (*) on that. However, the first paper took over 5 years to come out, and it’s not clear what the status of the other two is. There’s a lot of the second paper written, and I think we have a lot better idea of what’s going on in the full TQFT now for the third paper. However, I don’t quite know whether they’ll reach the light of day or not.

(*) So we can’t disambiguate Roberts by just calling him Justin.

Posted by: Simon Willerton on September 4, 2007 1:59 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

The second paper involved perturbative calculations for the TQFT

Is this still referring to extended Chern-Simons?

calculating S-matrices and lots of fun stuff; the third paper was on the full TQFT

Wow! Sounds impressive. Are you anywhere close to constructing CS as a 3-functor already?

Posted by: Urs Schreiber on September 4, 2007 2:10 PM | Permalink | Reply to this

Re: More on Tangent Categories

Any candidates for a cotangent n-category?

Posted by: David Corfield on August 21, 2007 3:11 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Hmm - contangent vectors eat vectors and spit out numbers. In the categorical context, you’d need something that likes to eat arrows and spit out… what?

Urs is doing his stuff for a darn good reason; if he bumps into a darn good reason to get a categorical version of the cotangent bundle, let’s hope he notices that and reports back!

Posted by: John Baez on August 22, 2007 12:27 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

if he bumps into a darn good reason to get a categorical version of the cotangent bundle

I was thinking about this a lot, lately. I feel there is indeed a good motivation to think of cotangent categories. However, I still feel puzzled about what it all really is about, so that’s why I haven’t really talked much about it.

Indeed, I had a couple of paragraphs already written in reply to David’s question yesterday, when I realized that none of these thoughts were anywhere near the point where communicating them would actually lead to a decrease of intellectual entropy.

Originally, I thought that something like categorical cotangent bundles would be helpful to trace down why differential graded algebras are so omnipresent in physics.

But, we are understanding that all these differential graded algebras are really just the Koszul dual incarnation of the Lie version of $n$ -groupoids of physical configurations and/or states.

So the question is, for me: are all things cotangent best understood as just a more or less weird alternative point of view on just Lie $n$ -groupoids (and their tangent $n$ -groupoids)?

Or should one maybe try to understand that this “weird change of viewpoint” is actually not as weird. Maybe by relating it to a notion of cotangent categories.

I really don’t know at the moment. But maybe the vague remarks I just made trigger something in somebody.

If so, please trigger me back by dropping a comment here! :-)

Posted by: Urs Schreiber on August 22, 2007 12:43 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

What if we just tried a completely naive approach and tried to mimic $T^{*} X = Hom (T X, ℝ)$ ?

So, starting with the special case of $Σ G$ for some group $G$ ,

$T^{*} Σ G = Hom (T Σ G, ?) = Hom (G / / G, ?) .$

Then we might fall back on that old workhorse ? = Vect.

Posted by: David Corfield on August 22, 2007 1:22 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

I wouldn’t want to use $Vect$ here, that would somehow go against the grain of the picture which is emerging here, which is purely “combinatorial”.

But, I’d say the $n$ -category dual to the $n$ -category $C$ is $C^{*} : = {Hom}_{n Cat} (C^{op}, (n - 1) Cat),$ i.e. that of all pre $n$ -sheaves on $C$ .

It might actually be reasonable to think $T^{*} C : = (T C)^{*}$ this way.

Posted by: Urs Schreiber on August 22, 2007 1:40 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

So,

$(T Σ G)^{*} = (G / / G)^{*} = {Hom}_{Cat} ((G / / G)^{op}, Set) .$

Oh, does 2 show up a lot in duality theorems as it’s $(- 1) - Cat$ ?

Peter Johnstone mentions its many guises as a ‘schizophrenic’ object (which we were considering renaming ‘Janusian’ or ‘Janus-faced’ after Tom Leinster’s valid objection). Can Set be seen similarly as Janusian, under different guises?

Speaking of renaming things, perhaps we should claim ‘dual’ for the sense you’ve just given, and call ‘opposite’ what’s sometimes called ‘dual’.

Posted by: David Corfield on August 22, 2007 2:32 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Your ‘dual’ Lawvere calls ‘concrete duality’ for a particular choice of dualizing object. ‘Opposite’ he calls ‘formal duality’.

Then, we read, “a large part of the study of mathematics … may be considered as the detailed study of the extent to which formal duality and concrete duality into a favorite $V$ correspond or fail to correspond.”

Posted by: David Corfield on August 22, 2007 3:48 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Your ‘dual’ Lawvere calls ‘concrete duality’ for a particular choice of dualizing object. ‘Opposite’ he calls ‘formal duality’.

Interesting. I vaguely rememeber you having talked about this before, but I completely forget the details.

(But if you fix the link you wanted to provide, I’ll try to follow it ;-)

What does “opposite” refer to right at the moment? Just reversal of arrows?

Are there a couple of easily accessible concrete examples where we could see this relation between formal and concrete duality in action, usefully?

Posted by: Urs Schreiber on August 22, 2007 4:05 PM | Permalink | Reply to this

Re: More on Tangent Categories

I fixed the link. It was just to a post where I quoted from Lawvere and Rosebrugh’s ‘Sets for Mathematics’.

What happens to opposites in higher categories? Do you just reverse everything?

I can’t think of a situation where the Hom from one category to another is equivalent to the opposite.

Posted by: David Corfield on August 22, 2007 8:15 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

I can’t think of a situation where the Hom from one category to another is equivalent to the opposite.

Here’s a toy 2-enriched example: let X be a sup-lattice (in a topos, $Set$ if you prefer), and let 2 denote the subobject classifier. Then the opposite $X^{op}$ is sup-lattice-isomorphic to hom( $X$ , 2), where this hom is the poset of sup-preserving maps. (It also realizes an equivalence between the category of sup-lattices and its opposite, of course.)

Posted by: Todd Trimble on August 22, 2007 8:54 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

Oh, does $2$ show up a lot in duality theorems as it’s $(- 1)$ −Cat?

Ah, very interesting remark. I hadn’t thought about this.

Right, by the definition I just proposed, we find that for $S$ any set (0-category) the “dual set” is $S^{*} = {Hom}_{Set} (S, {0,1}) .$ But that’s just the set of subsets of $S$ !

Fun.

Posted by: Urs Schreiber on August 22, 2007 4:09 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

David writes:

Oh, does 2 show up a lot in duality theorems as it’s $(- 1) - Cat$ ? Peter Johnstone mentions its many guises as a ‘schizophrenic’ object (which we were considering renaming ‘Janusian’ or ‘Janus-faced’ after Tom Leinster’s valid objection). Can Set be seen similarly as Janusian, under different guises?

Here’s one 2-categorical duality in which $Set$ appears as an <ahem> ambimorphic or Janusian object: between the 2-category of Cauchy complete categories on one side, and the 2-category of presheaf toposes and bicontinuous functors on the other.

Sweeping aside any set-theoretic subtleties, we have a 2-categorical Galois connection

\frac{A \overset{bicont}{\to} {Set}^{C}}{C \to Bicont [A, Set]}

where $A$ is complete and cocomplete. For $A = {Set}^{C}$ , $Bicont [{Set}^{C}, Set]$ gives the Cauchy completion $\hat{C}$ of $C$ . And for such $A$ , we have $A ≃ {Set}^{Bicont [A, Set]}$ .

A more interesting example is given by Gabriel-Ulmer duality. Rather than attempt to explain this, let me just refer to a nice paper which encapsulates a broad class of such dualities:

C. Centazzo and E.M. Vitale, A duality relative to a limit doctrine, TAC vol. 10 no. 20 (2002).

Posted by: Todd Trimble on August 22, 2007 7:23 PM | Permalink | Reply to this

Re: More on Tangent Categories

Thanks. I wonder if there’s a category which is more U(1)-ish to provide a categorified Pontryagin duality.

Posted by: David Corfield on August 22, 2007 8:27 PM | Permalink | Reply to this

Re: More on Tangent Categories

$MathML-enabled post (click for more details).$

I wonder if there’s a category which is more $U (1)$ -ish

John offered us the category of $U (1)$ -phased sets $Set ↓ U (1) .$

Since we were talking about tangent categories, it might be of interest to notice that groupoids over the tangent category $T Σ U (1) = T_{•} Σ U (1) = INN (U (1)) = U (1) / / U (1)$ of $U (1)$ , play a very similar role.

And it might be remarkable that such groupoids appear automatically as we take sections of differentials of $U (1)$ -valued functors. In this sense:

suppose $F : C \to Σ U (1)$ is a functor on some category $C$ which sends each object to the single object of $U (1)$ and each morphism to an element in $U (1)$ .

Then, by the operation which I denote $δ$ and argued to be the right notion of differential applied to functors (section 3.2), we find that $δ F : C \to Grpd$ is a functor which sends each object to the groupoid $U (1) / / U (1)$ , i.e. $δ F : (x \overset{γ}{\to} y) \mapsto (U (1) / / U (1)) \overset{F (γ)^{*}}{\leftarrow} (U (1) / / U (1)) .$ A section of this functor, to be thought of literally (therefore the name) as a section of the $U (1)$ -bundle with connection represented by $F$ is a morphism into $F$ , hence another groupoid-valued functor $E : C \to Grpd$ with a transformation $e : E \to δ F .$ By the magic of tangent categories (and this is at the heart of the reason for looking at them in this context here) such a transformation is entirely determined, already, by its values over objects (over morphisms it will then automatically assign the corresponding “covariant derivative” ).

But over any object $x$ , such a section is nothing but a $U (1) / / U (1)$ -phased groupoid: $e (x) : E (X) \to U (1) / / U (1) .$ To potentially see that this is potentially a good thing, concentrate for a moment on the case that these groupoids $E (x)$ all have no nontrivial vertex groups, such that they are equivalent to just a set of isomorphism classes of objects. In this case a section as above is a function on $Obj (C)$ with values in $U (1)$ -phased sets.

According to some general expectations floating around the $n$ -Café, this is a good way to think of a $U (1)$ -valued function.

I am hoping that the general nonsense of tangent categories combined with the general nonsense on curvature of transport which I am working on will, this way, actually neatly make contact with the Tale – and help free the world from vector spaces ;-)

Anyway, I just thought I might mention this in the present context.

Posted by: Urs Schreiber on August 22, 2007 9:04 PM | Permalink | Reply to this

Re: More on Tangent Categories

Hi David,
So this might be completely off base, but wouldn’t it be more inline with the philosophy here to parameterize the cotangent bundle over some kind of target object, like the one Isham uses in his recent topos papers to take the place of the real numbers?

I think what I’m grasping at is how would one do “classical” diff geo based upon a topos other than Set? Surely someone has done that before.

Posted by: Creighton Hogg on August 22, 2007 6:36 PM | Permalink |

The n-Category Café

Skip to the Main Content

August 21, 2007