The n-Category Café

Multiplicative Structure of Transgressed n-Bundles

Posted by Urs Schreiber

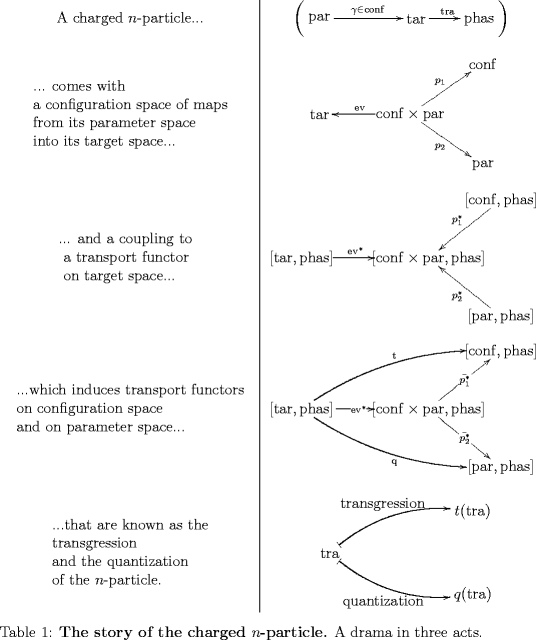
Remember the drama of the charged $n$-particle?

An $n$-particle of shape $\mathrm{par}$ propagating on target space $\mathrm{tar}$ and charged undern an $n$-bundle with connection given by the transport functor $\mathrm{tra} : \mathrm{tar} \to n\mathrm{Vect}$ admits two natural operations: we may either quantize it. That yields the extended $n$-dimensional QFT of the $n$-particle, computing the $n$-space of its quantum states $q(\mathrm{tra}) : \mathrm{par} \to n\mathrm{Vect}$.

But we may also, instead, transgress the $n$-bundle background field on target space to something on the particle’s configuration space.

For instance, a closed string (a 2-particle) charged under a Kalb-Ramond gerbe (a 2-bundle) gives rise to a line bundle (a 1-bundle) on loop space. I once described this in the functorial language used here in this comment.

But, and that’s the point of this entry here, these transgressed $n$-bundles have certain special properties: they are multiplicative with respect to the obvious composition of elements of the configuration space of the $n$-particle.

I have neither time nor energy at the moment to give a comprehensive description of that. What I do want to share is this:

With Bruce Bartlett I was talking, by private email, about the right abstract arrow-theoretic formulation to conceive multiplicative $n$-bundles with connection obtained from transgression on configuration spaces. It turns out that a $n$-transport functor is multiplicative if it is monoidal with respect to a certain natural variation of the concept of monoidal structure which is applicable for fibered categories.

In the file

The monoidal structure of the loop category

I spell out some key ingredients of how to conceive the situation here for the simple special case that we start with a 1-functor and transgress it to a “loop space”.

There is nothing particularly deep in there, but it did took us a little bit of thinking to extract the right structure here, simple as it may be. So I thought we might just as well share this with the rest of the world.

And, by the way, I will be on vacation in southern Spain until July 20.