The Inner Automorphism 3-Group of a Strict 2-Group
Posted by Urs Schreiber
David Roberts and I would like to share the following text:
D. Roberts, U.S.
The inner automorphism 3-group of a strict 2-group
arXiv:0708.1741
Abstract
Any group gives rise to its 2-group of inner automorphisms, . The nerve of this is the universal -bundle. Similarly, for every 2-group there is a 3-group of inner automorphisms. We construct this for any strict 2-group, discuss how it can be understood as arising from the mapping cone of the identity on and show that it fits into a short exact sequence of strict 2-groupoids. We close by indicating how this makes the universal -2-bundle.
I am very glad that David Roberts joined me on the quest for inner peace – I mean: for inner automorphisms. I very much enjoyed this fruitful exchange. All by email, of course, and intercontinental, as befits a true blog community.
David has a bunch more notes on how everything and more works in the world of simplicial groups, making in particular the relations to Brano Jurčo’s work Crossed Module Bundle Gerbes; Classification, String Group and Differential Geometry more manifest.
We are grateful to Jim Stasheff for accompanying this capital endeavour with his guidance, and for making us relate it, by the mapping cone construction, more closely to the lower case business, which we have been involved in recently.
Related entries:
I started thinking about in my first entry titled -Curvature. There the point was that we can understand the differential 2-cocycles given by Breen and Messing as morphisms of 3-functors, where plays the role of the 3-curvature of the pseudo transport 2-functor , following the general mechanism described in Sections, States, Twists and Holography.
The trivializability of is crucial here: it makes a flat 3-transport, which is the Bianchi identity in this context, as described in the second entry called -Curvature as well as in Curvature, the Atiyah Sequence and Inner Automorphisms.
But this relation to 3-curvature is not mentioned in the present text. In fact, at the moment I am not completely sure how it relates conceptually to the fact – which we do discuss – that plays the role of the universel -2-bundle. It feels a litte embarrassing, since there ought to be an obvious relation. But at the moment it escapes me.
-3-transport is supposed to give the right notion of parallel transport in particular for spinning strings, being the integrated version of the 3-connections discussed in terms of Lie -algebras in Connections on String-2-Bundles, following the general mechanism described in Chern Lie (2n+1)-algebras.
(But notice that there seem to be also much more mundane applications: in The -Café quantum conjecture I indicated how ordinary -bundles with connection can be conceived in terms of -transport, thereby making the appearance of “phases” (i.e. elements in ) a phenomenon emerging from more ordinary ingredienty like the integers and the reals. )
In fact, the realization described in Derivation Lie 1-Algebras of Lie -Algebras that the Lie -algebra of inner derivations of any Lie -algebra arises as the mapping cone of the identity on motivated David Roberts and myself, greatly influenced by Jim Stasheff’s guidance, to pursue what is now advertized as one of the two main results of our text: that is indeed the nonabelian mapping cone, in the sense of Conduché, of the identity on .
Finally, on a more speculative note, it seems remarkable that the construction of short exact sequences of Lie -algebras for every transgressive Lie -cocycle is very much controlled by the exact sequence of groupoids, for any Lie (1-)group, which plays the role of the universal -bundle.
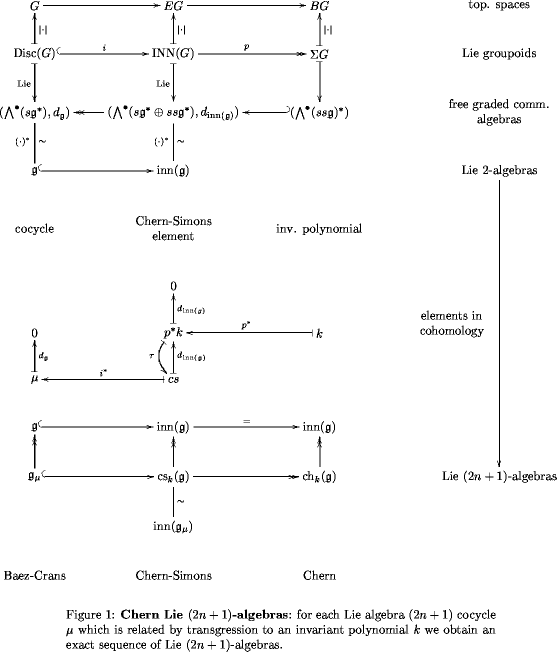
This makes one naturally wonder if this entire construction has a counterpart when we replace the sequence by the sequence for any strict Lie 2-group, which plays the role of the universal -2-bundle.
This should involve something like a categorification of the concept of a Lie algebra cocycle, namely a Lie 2-algebra cocycle, as well as the related notions of transgression and invariant polynomials.
I have the vague suspicion that this is what will finally allow to put the supergravity Lie 3-algebra in its proper home, using the fact that the Poincaré Lie algebra, which the supergravity Lie 3-algebra is an extension of, being a semidirect sum, really wants to be regarded as a strict Lie 2-algebra. But this I still haven’t figured out yet.

Re: The inner automorphism 3-group of a strict 2-group
I should point out here one question, which we haven’t been able to fully clarify, but a discussion of which would be good:
as described at length, the 3-group is essentially just the sub-3-group of the full autormorphism 3-group containing all those automorphism which arise by conjugation with objects in .
But not quite. The point is that we do distinguish in two objects to be different, if they are different as objects of but even if conjugating by them happens to lead to the same automorphism (so, if they differ by something “in the center”).
We describe explicitly how is constructed. What is missing is a nice general 1-line abstract definition, which captures this funny little add-on, which says that we have to distinguish objects even if they have the same conjugation action.
In fact, in one dimension lower there is an indication for how it should work. But I can’t quite see how to generalize this:
There the point is this: for any ordinary group, we shouldn’t just look at automorphisms and then demand them to be inner, etc., but we should just say this: look at the group of transformations of the form under horizontal composition.
That solves the problem: the mere existence of such a transformation exactly constrains the lower automorphism to be inner. Moreover, the particular choice of transformation from the identity to that automorphism distinguishes between conjugations by different morphisms which lead to the same inner automorphism.
So, I was hoping to be able to say, strictly, that , for any -group is something like the -group of transformations of the above form.
But
a) I am not entirely sure yet how to formulate this in general
b) while it gives the expected result for , I don’t see how it gives (up to equivalence), our desired construction (described at detail in the paper) of .
I’ll need to further think about this. If anyone has any comments on this, I’d be very grateful. Probably we are just missing the obvious.