The n-Category Café

Arrow-Theoretic Differential Theory III: Higher Morphisms

Posted by Urs Schreiber

In Arrow-Theoretic Differential Theory, Part II I argued that we need to pass to tangent categories in order to understand, not just $n$-curvature, but also higher morphisms of Lie $n$-algebras.

In Vienna John Baez quizzed me about these ideas, thereby leading me to the more refined insight which I mentioned in More on Tangent Categories.

This insight, which involved making explicit a fact and a construction which I had already been using in a way but not truly realized myself, I have now started to seriously incorporate while revising the provisional Structure of Lie $n$-algebras.

Since it all seems to work out quite nicely – unless I am making some dumb mistake – here is an update on that matter:

Higher Morphisms of Lie $n$-Algebras from Arrow-Theoretic Differential Theory

Abstract.

We would like to achieve a good explicit understanding of higher morphisms of Lie $n$-algebras. We notice that various formerly puzzling aspects of this seem to become clearer as one passes from Lie $n$-algebras $g_{(n)}$ to their Lie $(n+1)$-algebras of inner derivations $\mathrm{inn}(g_{(n)})$ in a certain way. Using this, we define higher morphisms of Lie $n$-algebras explicitly and in general. These should constitute an $(\infty,1)$-category. While we fall short of verifying this in full generality, we do obtain the Baez-Crans 2-category of Lie 2-algebras [1] in the special case where we restrict everything to Lie 2-algebras.

Introduction

The crucial point of the discussion is possibly best exhibited by the following simple example:

Let $G$ be any abelian group. Write $\Sigma G$ for the corresponding one-object groupoid, and $\Sigma^2 G$ for the corresponding one-object one-morhisms 2-groupoid. Write $\mathrm{INN}(G)$ for the codiscrete groupoid over $G$.

We have canonically [2] a short exact sequence $$G \hookrightarrow \mathrm{INN}(G) \to \Sigma G$$ of groupoids.

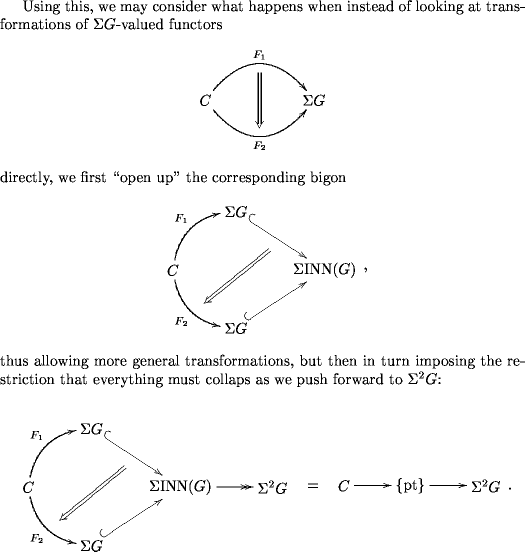
For this simple example, it is easy to see that the transformations obtained by first “opening up” and then restricting as above are in bijection with the ordinary transformations of the original functors.

As we pass to higher $n$-groups, though, the situation becomes more flexible.

We find that at the level of Lie $n$-algebras, it is only the “opened up” transformations which have a good direct description in the first place. We here define ordinary higher morphisms of Lie $n$-algebras by the analogue of “opened up” and then restricted transformations.