This Week’s Finds in Mathematical Physics (Week 260)
Posted by John Baez
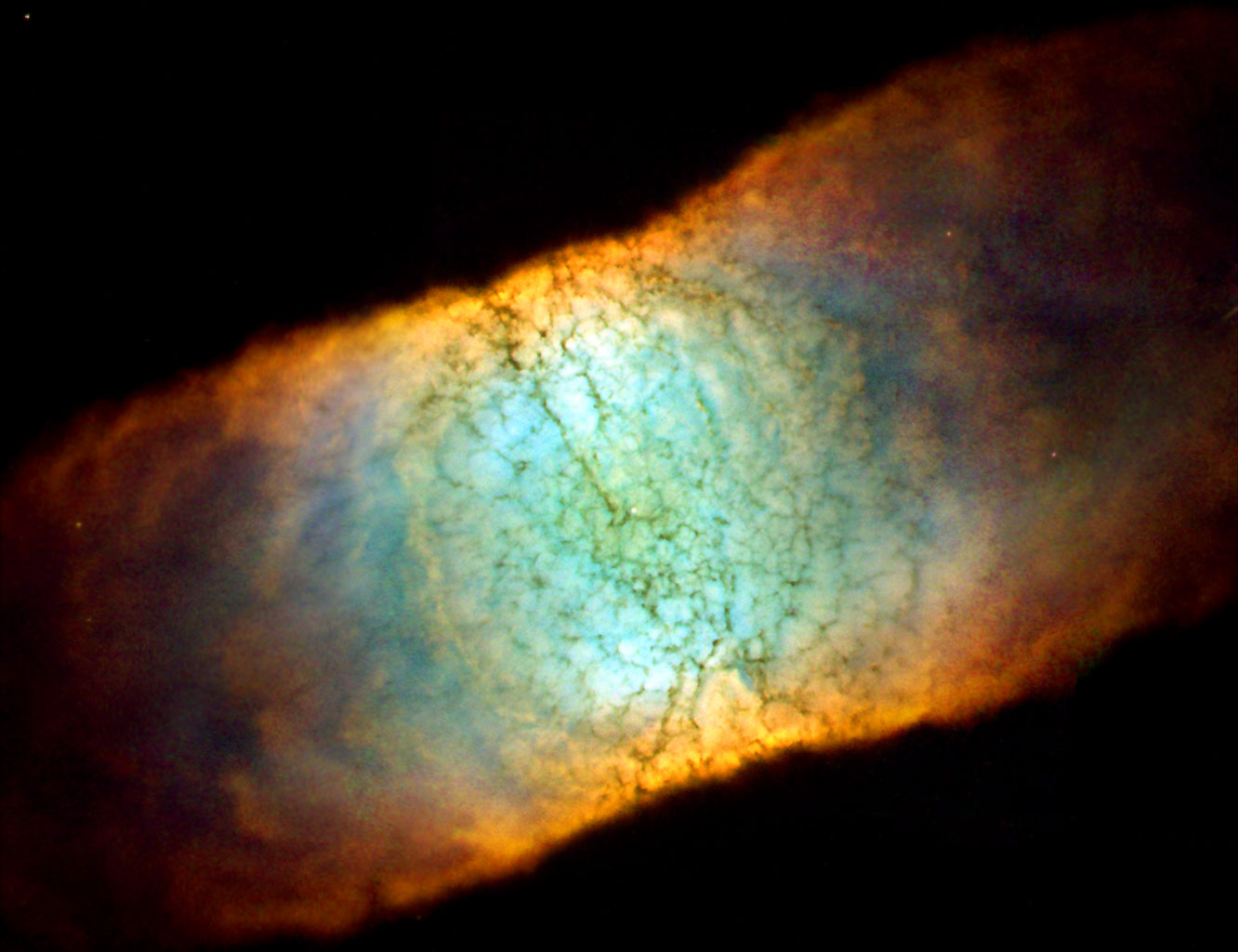
In week260 of This Week’s Finds, learn about the Vishniac instability in the Retina Nebula:
Then try my Christmas eve guide to free books on math and physics. There are more and more available! Soon those expensive textbooks will be obsolete. Here’s a nice illustration of Taylor series for the sine function, from Robert Nearing’s online book Mathematical Tools for Physics:

And finally: the ‘exceptional series’ of Lie algebras.
Posted at December 25, 2007 3:15 AM UTC
Re: This Week’s Finds in Mathematical Physics (Week 260)
Yesterday I bet someone that John would post something here on Christmas day. I won! And a wonderful festive TWF it is.
There are a few more free category theory books in the Reprints series of Theory and Applications of Categories.
Merry Christmas to all!