Local Nets from 2-Transport
Posted by Urs Schreiber
While listening to AQFT talks last Friday I further developed the thoughts that I started talking about in
Oberwolfach CFT, Arrival Night, Algebra of Observables and Sheaves of Observables.
I wrote up a note in which the passage from -dimensional functorial QFT to the corresponding AQFT local net of observables is described in more detail:
On nets of local operators from 2-transport
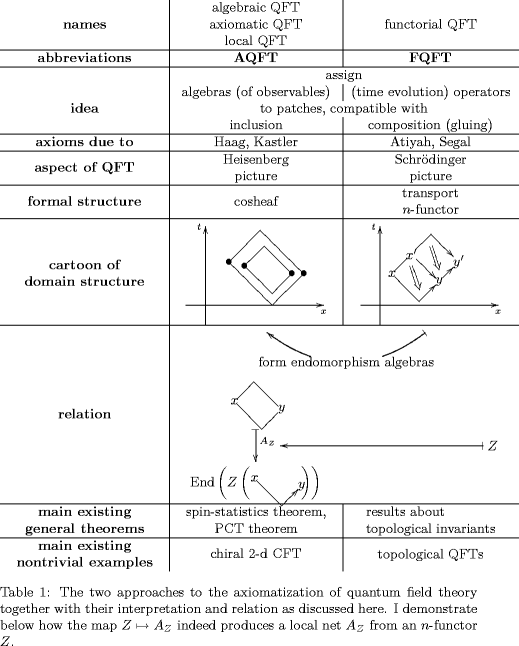
Abstract. I would like to understand how the axioms of a local net of observable algebras follow from those of a transport -functor with values in -vector spaces. I suggest that local nets of algebras result when applying to an -vector transport a categorified version of the transition from the Schrödinger to the Heisenberg picture of quantum mechanics.
Here I consider some simple aspects of this question for . I show that every extended 2-dimensional QFT gives rise to a net of local monoids on 2-dimensional Minkowski space. The construction has an obvious generalization to arbitrary .
Introduction.
Nets of operator algebras (you can find details for a 1-dimensional net, which is slightly different from what I am considering here, discussed in the entry CFT in Oberwolfach, Monday morning) are functors from subcategories of open subsets of pseudo-Riemannian spaces to a poset of subalgebras of some ambient algebra, usually that of bounded operators on some Hilbert space.
Using the pseudo-Riemannian structure, one singles out those pairs of subsets which are spacelike separated. A net of operators is called local if the subalgebras assigned to spacelike separated subsets commute with each other.
Nets of local operator algebras have been introduced in order to formalize the concept of the algebra of observables in quantum field theory.
Out of the study of these structures a large subfield of mathematical physics has developed, which is equivalently addressed as algebraic quantum field theory, or as axiomatic quantum field theory or as local quantum field theory, but usually abbreviated as AQFT.
To my mind, all three of these terms as such would equally well describe also what is probably the main alternative parallel development, as endeavours towards giving quantum field theory a good axiomatic framework: the study of representations of cobordism categories.
While this approach did apparently not receive a canonical name so far, I am used to referring to it as \emph{functorial quantum field theory}. Here I shall abbreviate that as FQFT.
An obvious question is: What is the precise relation between AQFT and FQFT? I am not aware of any explicit attempt to answer this. To a large extent, developments in AQFT and FQFT have been, in the past, rather disconnected.
The most successful – strikingly successful – application of AQFT has actually been to chiral 2-dimensional conformal field theory. Here AQFT has provided a rich collection of results, notably important classification results. (On the other hand it is still unclear, as far as I am aware, how to realize the main motivating example, 4-dimensional gauge theory of Yang-Mills type, in the language of AQFT.)
The most well known application of FQFT is to topological quantum field theory (TQFT): the theory of representations of categories of cobordisms up to diffeomorphism. This goes so far that some people have expressed the believe that FQFT = TQFT instead of FQFT TQFT. While this is actually not the case – since whenever we have a category of cobordisms with extra structure (conformal, Riemannian) the notion of FQFT on it makes sense – it is true that the tractability of FQFT away from the topological realm drops sharply.
But progress is visible. The closest possible point of contact between AQFT and FQFT obtained so far is possible the description of full 2-dimensional conformal field theory in terms of a topological QFT internal to the representation category of a chiral net, as given by Fuchs, Runkel and Schweigert (FRS).
As indicated in Towards 2-functorial CFT how at least parts of the topological aspect of the FRS description arises from a “local trivialization” of an extended FQFT transport 3-functor. The discussion to follow can be regarded as providing also the connection between this -functor and the chiral nets. But many details remain to be better understood.
In any case, it is clear that both AQFT and FQFT are relevant for understanding what quantum field theory really is. Since there is just one reality, there should be a way to relate them systematically.
Here I shall try to present evidence which suggests that the situation is as indicated by the following slogan:
AQFT is to FQFT like the Heisenberg picture of quantum mechanics is to the Schrödinger picture. Forming endomorphism algebras provides a systematic map from FQFT to AQFT.
For this to work, it is important to understand FQFT as what is sometimes called extended functorial QFT: originally FQFT was conceived as being about functors from cobordisms categories to some category of vector spaces. But later it was realized that, more generally, one wants to model extended cobordsisms, which live in higher categories. Hence an extended -dimensional functorial quantum field theory is an -functor.

Re: Local Nets from 2-Transport
This is very interesting Urs. I’d like to know : how restrictive is it that you are using diamond shaped regions instead of more general open sets?
Also, you define the FQFT as a 2-functor from the path 2-category to Vect. However the path 2-category only contains lightlike paths. Can you do it for the “full” path 2-category? I guess it should be the one which only contains timelike paths.