On BV Quantization, Part VIII

November 29, 2007

Posted by Urs Schreiber

$MathML-enabled post (click for more details).$

A good way to understand the relevance and meaning of the trinity of

ghosts – fields – anti-fields

in the BV-formulation of quantum field theory (part I, II, III, IV, V, VI, VII) is to interpret the story of the charged

n

-particle in the world of Lie

∞

-algebroids (as opposed to Lie

∞

-groupoids), which have a restriction on the sign of the degrees of their morphisms, but then form the configuration space of fields by taking the internal hom in the category of arbitrarily graded things.

This is, to my mind, how to interpret one of the crucial points of AKSZ: The Geometry of the Master Equation and Topological Quantum Field Theory.

Here I start to talk about that, but it will probably take me more than one installment. Progress will be documented in On Lie $∞$ -modules and the BV complex.

$MathML-enabled post (click for more details).$

Recall, maybe from QFT of the Charged $n$ -Particle: Definition, that quantum (field) theory is the study of the following setup:

- a Lie $∞$ -category $par$ , called the parameter space or the $n$ -particle

- a Lie $∞$ -category $tar$ , called the target space

- an $∞$ -functor $tar \to phas$ called the background field

(and possibly a symplectic structure on some of the $∞$ -groupoids, but this will be the topic of later installments)

which allows to form the configuration space

$conf : = hom (par, tar) .$

The background field transgresses to this configuration space, where it then forms the (non-kinetic part of) the action of the $n$ -particle.

In practice, instead of Lie $∞$ -groupoids one will often turn to the corresponding Lie $∞$ -algebroids (see for instance On Lie $N$ -tegration and Rational Homotopy Theory).

Depending on various conventions, these are structures on (co)chain complexes of non-negative degree, and that makes good sense:

the stuff in degree $k$ are the tangents to the space of $k$ -morphisms of the original $∞$ -groupoid.

But when we forget categories and just look at chain complexes, then there is nothing more natural than allowing arbitrary gradings. This hence corresponds to considering categories with negative morphisms.

Luckily the Wizards have thought of that before. And have come up with a name for them: $ℤ$ -categories.

As far as I understand, there are currently precisely two persons on this planet who have seriously thought about $ℤ$ -categories: John Baez and Jim Dolan. Though the point is that in disguise at least $ℤ$ -groupoids are well known to topologists: $ℤ$ -groupoids correspond to spectra.

But let’s not worry about $ℤ$ -categories too much at this point. While they nicely highlight the depth of the step from non-negative to arbitrary grading, performing that step itself in the linearized world of complexes and dg-algebras is very simple. (Maybe too simple, actually. Nobody seems to discuss the deep importance of this simple step.)

Then we obtain a picture of this sort:

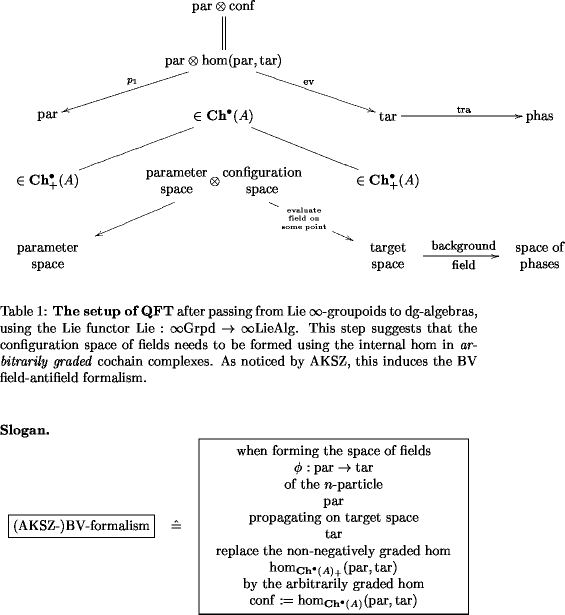
I have tried to summarize some of the properties of the category of (co)chain complexes that we need in section 2.

So before actually going in to the AKSZ description of the charged $n$ -particle, let’s have another look at our toy example setup from BV for Dummies and On Noether’s Second (BV, Part VI).

Recall that there we were dealing with a setup where

- configuration space $conf = X$

is an ordinary manifold, and where the action

- $S \in C (X)$

is an ordinary function on that manifold.

This induced for us the BV-complex which was a dg-algebra extension of this simple situation

$\begin{matrix} 0 & \overset{d ∣}{\to} & M_{- 2}^{*} & \overset{d ∣}{\to} & M_{- 1}^{*} & \overset{d ∣}{\to} & M_{0}^{*} & \overset{d ∣}{\to} & V_{1}^{*} & \overset{d ∣}{\to} & 0 \\ 0 & \to & \ker (d S (\cdot)) & ↪ & Γ (T X) & \overset{d S (\cdot)}{\to} & C^{∞} (X) & \overset{ρ}{\to} & C^{∞} (X) \otimes g^{*} & \to & 0 \\ - 2 & - 1 & 0 & 1 \\ antighosts & antifields & fields & ghosts \\ (three - & - & - vector - & - & space) & (Lie algebra) \\ (- - - & - & - 3 - module - & - & - - -) \end{matrix}$

(Here the $d ∣$ denotes the result of restricting domain and codomain of $d$ to be $V^{*} \otimes M^{*}$ (i.e. just the first tensor power). )

(which I have taken from Modules for Lie $∞$ -Algebras).

In order to fully appreciate the AKSZ-BV construction for the charged quantum $n$ -particle, we need to familiarize ourselves with the dual picture of this BV complex (section 4.3.5):

By simply working out what the dual differential is, one finds

With that simple example in mind, we should now see what happens when we form the configuration space of worldvolume fields of the charged $n$ -particle using the internal hom in arbitrarily graded chain complexes.

But this I’ll discuss next time.

Posted at November 29, 2007 8:46 PM UTC

TrackBack URL for this Entry: http://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/1518

50 Comments & 3 Trackbacks

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Cool stuff! You are clearly becoming quite a Wizard^TM yourself.

One pathetically minor question: when you write

$Lie : ∞ Gpd \to ∞ {LieAlg}^{*}$

what’s the meaning of that little asterisk? It doesn’t mean ‘dual’, does it? Is it hinting at a footnote I can’t find??

Posted by: John Baez on November 30, 2007 2:05 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

John said:

One pathetically minor question: when you write

$Lie : ∞ Grpd \to ∞ {LieAlg}^{*}$

whats the meaning of that little asterisk?

Sorry, that’s a typo. .

It’s a remnant of a thought process in which I first wanted to talk about a functor from $∞$ -groupoids to Chevalley-Eilenberg-algebras of Lie $∞$ -algebras.

But, while technically important, this is not something that should be dealt with in a semi-sentence in the caption of the above figure.

So I have erased that little star now. Thanks for catching that.

Posted by: Urs Schreiber on November 30, 2007 11:09 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

I thought I’d already asked this, but in this context
why would you want to replace Hom by a \otimes?

and what does the word `induces’ as in AKSZ induces
mean?

abd remind me what is in AKSZ beyond BV
except for extension of the `manifold’ language?

Posted by: jim stasheff on November 30, 2007 2:06 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

I thought I’d already asked this, but in this context why would you want to replace “ $Hom$ ” by a “ $\otimes$ ”?

I gather you are asking why I care about the fact that – if everything is suitably finite – chain complexes are compact closed such that the internal hom satisfies the condition

$hom (V, W) ≃ W \otimes V^{*}$

familiar from the category of vector spaces (as we have discussed at some length here and here, which I summarize in detail in section 2.3 of my notes, and for detailed discussion of which I am very grateful to Todd Trimble, who helped me look at it more systematically, and, finally ;-), also to John Baez)?

If so, the answer is: because it is a very handy fact, for instance for the following reasons:

- It is exactly the formal version of the way many people write a superfield $ϕ : V \to W$ - not as an element of a hom-space in general, but explicitly as an element of $W \otimes V^{*}$ , namely an expression they write like $ϕ = ϕ^{n} (x) + ϕ^{n - 1} (x_{1}) + ϕ^{n + 1} (x_{- 1}) + \dots$ with $ϕ^{i} \in W$ and $x_{i} \in V^{*}$ . Like on the bottom of p. 11 of Dmitry’s review of AKSZ-BV.

- Moreover, using this fact we can transate Chevalley-Eileneberg algebras of Lie $∞$ -algebras, which come to us as complexes of homs $CE (g) = (\dots \to hom (g \land g, B) \overset{d_{CE}}{\to} hom (g \land g \land g, B) \to \dots)$ into qDGCAs on $\land^{∞} (g^{*} \otimes B)$ which is not only convenient for practical computations but also – as I am beginning to try to argue in Something Like Lie-Rinehart $∞$ -pairs and the BV-complex – apparently a way to understand the BV-complex as a Lie Rinehart $∞$ -pair and, in the process, obtain one explanation/interpretation of the meaning of arbitrarily (positively and negatively) graded dg-algebras (“Lie $ℤ$ -groupoids”, if you like): the positive part, $g^{*}$ , is a Lie $∞$ -algebra which acts on the chain complex $B$ in the non-positive degree.

That’s all. I do understand that $hom (V, W) ≃ W \otimes V^{*}$ relies on the complex being bounded and of finite rank in each degree (as Todd kept emphasizing, for instance here). But it’s still useful.

Posted by: Urs Schreiber on November 30, 2007 11:43 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

Oh, OK for that application
but it really should be
(∧ ∞g)*⊗B)
instead of
∧ ∞(g *⊗B)
and that would avoid some of the technical conditions you and Todd mention

Posted by: jim stasheff on November 30, 2007 1:50 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

but it really should be $(\land^{∞} g^{*}) \otimes B$ instead of $\land^{∞} (g^{*} \otimes B)$

Thanks for mentioning this! I tried to discuss this issue before, but failed to make myself clear:

I understand that (when everything is suitably finite), from $\dots \to hom (g \land g, B) \overset{d_{CE}}{\to} hom (g \land g \land g, B) \to \dots$ we get, at face value, a differential on $\land^{∞} (I \oplus g^{*}) \otimes B .$

But this extends, trivially, to all of $\land^{∞} (g^{*} \oplus B)$ doesn’t it?

And after being puzzled about what to make of this for a while, it seemed to occur to me that what is actually going on in BV formalism is that we form the full $\land^{∞} (g^{*} \oplus B)$ and then put a differential on that.

So this struck me as relevant. In particular, since the expression $\land^{∞} (g^{*} \oplus B)$ is in a way quite more “elegant” or “natural” than $\land^{∞} (I \oplus g^{*}) \otimes B .$ The reason is that, as it happens,

- $g^{*}$ is always of positive degree

- while $B$ is always of non-negative degree

- such that they exactly fit together to form a complex

$g^{*} \oplus B$

of arbitrary degree, with no overlap.

This seems to be good, because also when we are forming, for instance, the internal hom $hom (V, M)$ we obtain one single thing in arbitrary degree. If we like, we can separate this as $g^{*} \oplus B$ , and this way identify ghosts, fields and antifields. But the way it arises is as one unified thing, and it would seem unnatural (and, I think, for the general case even impossible, but this I am not sure about right now) to have the dg-structure on $hom (V, W)$ equivalently encoded in one on $\land^{∞} (I \oplus g^{*}) \otimes B$ .

So, you see, this issue you address is one I kept wondering about when starting to think about this a while ago. Let me put it like this:

how do we say “Lie $∞$ -algebra” in an arrow-theoretic way internal to cochain complexes? We say:

there is a positively graded cochain complex $g^{*}$ together with an extension of the differential on $\land^{∞} (I \oplus g^{*})$ to a complex $(\land^{∞} (I \oplus g^{*}), d_{CE})$ such that the canonical projection $\begin{matrix} (\land^{∞} (I \oplus g^{*}), d_{CE}) \\ ↓ \\ g^{*} \end{matrix}$ still exists (i.e is still a cochain map).

This is equivalent to saying that we define a list of maps $d_{0} : g^{*} \to g^{*} [- 1]$ $d_{1} : g^{*} \to (g^{*} \land g^{*}) [- 1]$ $d_{2} : g^{*} \to (g^{*} \land g^{*} \land g^{*}) [- 1]$ $⋮$ of “co-arity” $0 \leq n < ∞$ such that $d_{0} : g^{*} \to g^{*} [- 1]$ coincides with the differential on $g^{*}$ and which together form a map $d : g^{*} \to \land^{∞} (I \oplus g^{*}) [- 1]$ which we extend to a differential on all of $d : \land^{∞} (I \oplus g^{)} \to \land^{∞} (I \oplus g^{)} .$

Sorry for boring you with this, this is just a triviality formulated in a verbose way. But I am just trying to make myself clear, which I think I failed to do before.

Namely if we now think about what

a) people do in the BV literature

b) people do in the lietarure on $L_{∞}$ -modules

we can think of both a) and b) as summarized neatly by just repeating the above construction, with the non-negatively graded cochain complex $I \oplus g^{*}$ everywhere replaced by an arbitrary cochain complex $g^{*} \oplus B .$

Maybe I am seeing ghosts (pun intended). But right now I am pretty fond of this (admittedly simple) idea (but also simple ideas need to be thought).

There seems to be a triangle emerging

$\begin{matrix} ℤ - groupoids \\ ↗ & ↘ \\ Lie - Rinehart ∞ - modules & \to & BV - complexes \end{matrix}$

Somehow.

Posted by: Urs Schreiber on November 30, 2007 3:32 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

It only occurs to me now that Jim’s remark above to which I gave a long-winded reply is apparently caused by another typo of mine.

Argh.

It seems here I wrote $\land^{∞} (g^{*} \otimes B)$ instead of $\land^{∞} (g^{*} \oplus B) .$

Sorry for that.

Posted by: Urs Schreiber on November 30, 2007 7:22 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

My comment also meant something more substantive: i said

(Lambda g)* otimes B

instead of

(Lambda g*) otimes B

and that would avoid some of the technical conditions you and Todd mention.
N.B. g)* not g*)
ie. alternating multilinear functions
ass in the original Chevalley-Eilenberg

Posted by: jim stasheff on December 1, 2007 1:36 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

Urs wrote:

they write like
ϕ=ϕ n(x)+ϕ n−1(x 1)+ϕ n+1(x −1)+⋯
with ϕ i∈W and x i∈V *.

boy, did that confuse me
I thought that phi(x) meant the usul functional notation
but what Dmitry does is use (du)^i
to avoid confusion with du^i

Posted by: jim stasheff on November 30, 2007 2:03 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

boy, did that confuse me I thought that phi(x) meant the usul functional notation but what Dmitry does is use (du)^i to avoid confusion with du^i

Actually, I need to take back what I said about how that is an example of using $V^{*} \otimes W$ instead of $hom (V, W)$ .

Actually, what Dmitry has there is rather the $hom (V, W)$ version, obscured through the fact that he writes

$ξ^{a} = A^{a} d u + \dots$

instead of

$ϕ^{*} : ξ^{a} \mapsto A^{a} d u + \dots .$

I meant to point to some other literature, where people actually do use the $V^{*} \otimes W$ -notation. Let me try to seach for a better example…

Posted by: Urs Schreiber on November 30, 2007 7:34 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

and what does the word ‘induces’ as in “AKSZ induces” mean?

Okay, thanks for asking. This is the part I still needed to talk about in more detail. I became too tired and ended the entry before actually saying anything AKSZ-wise.

So this is what I mean by “induces”:

Let for instance

$par = T X = Lie (Π (X))$ be the tangent algebroid of a manifold, and let $tar = Poiss (Y, ω)$ be the Poisson algebroid on some other manifold $Y$ with symplectic form $ω$ , then the external Hom $Hom (par, tar)$ is precisely the space of Lie algebroid morphisms from $T X$ to $Poiss (X, ω)$ .

These algebroid morphisms turn out to be that subspace of the space of all maps from par to tar that can be regarded as the on-shell fields with respect to the action of the Poisson Sigma-model.

So, then one might want to find the corresponding BV formalism. What are the ghosts, what are the anti-ghosts, what is the BV differential, etc.

Now, AKSZ answer this question as follows: they say: the BV complex is simply obtained by not taking the external Hom, but by taking the hom $hom (par, tar)$ internal to arbitrarily graded complexes.

This contains the external Hom we had above, hence the solutions to the classical equations of motion, as the closed elements in degree 0 $Hom (par, tar) = Z^{0} (hom (par, tar)) .$ On top of that, it contains stuff in positive degree. This are the ghosts. And it contains stuff in negative degree. This are the anti-ghosts. It all drops out automatically from just forming the inner hom.

Compare the first paragraph in section 4 of Dmitry’s review.

And of course that does not depend on the Poisson sigma model. Choose another target, and get the BV complex for the corresponding field theory.

That’s what I mean by “AKSZ induces” the BV complex: we just form the configuration space of fields internally in arbitrarily grading $conf = hom (par, tar)$ and by just turning the crank out drop all ghost, fields and the BV differential on them.

P.S. I should add that I am glossing over the following point:

I keep talking about the homs in chain complexes. But what we really need here are homs in monoids in chain complexes, namely dg-algebras. This doesn’t change much about the general point here, but I need to eventually discuss this in more detail.

And at some point I will actually want to ask the wizards: what is known, from an abstract category-theory point of view, about the category $SymMonoids ({Ch}^{•} (A))$ of symmetric monoids internal to chain complexes ??

And in particular, that sub-category which has only qDGCAs as objects, namely dg-algebras which are free as graded commutative algebras.

Posted by: Urs Schreiber on November 30, 2007 12:09 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

Urs writes:

Thats what I mean by
AKSZ induces the BV complex: we just form the configuration space of fields internally in arbitrarily grading
conf=hom(par,tar)
and by just turning the crank out drop all ghost, fields and the BV differential on them.

P.S.
I should add that I am glossing over the following point:

I keep talking about the homs in chain complexes. But what we really need here are homs in monoids in chain complexes, namely dg-algebras. This doesn’t change much about the general point here, but I need to eventually discuss this in more detail.

I suspect you will need A_\infty maps, not just homs in dgas.

Like wise I’m amazed if the BV differential drops out, but I better read Dmitry first.

Posted by: jim stasheff on November 30, 2007 2:00 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Urs wrote:

And at some point I will actually want to ask the wizards: what is known, from an abstract category-theory point of view, about the category $SymMonoids ({Ch}^{•} (A))$ of symmetric monoids internal to chain complexes??

Okay, I can take a hint — you know I feel duty-bound to reply to any post that contains the word ‘wizard’, and you want me to say something helpful before you struggle through an enormous nasty calculation.

I’ve never heard of a “symmetric monoid”. You probably mean either “commutative monoid” or its categorified version, “symmetric monoidal category”.

I’m guessing you mean the former, though I have no idea what ‘ $Λ^{∞}$ ’ means, and that would be a helpful clue.

We can talk about commutative monoids internal to any symmetric monoidal category $C$ .

(For example: when $C$ is the category of chain complexes with its usual symmetric monoidal structure, these are supercommutative differential graded algebras.)

We always get a category $CommMon (C)$ of commutative monoids in $C$ , with monoid homomorphisms as the morphisms. This category is always symmetric monoidal in its own right.

We can talk about the free commutative monoid $S X$ on an object $X$ whenever $C$ also has coequalizers and (countable) coproducts:

$S X = 1 + X + X^{\otimes 2} / 2! + \dots$

You just take the symmetrized tensor powers of $X$ and add them up.

(For example, when $C$ is the category of chain complexes, $S X$ is the free supercommutative differential graded algebra on the chain complex $X$ .)

So, under these hypotheses, we get a ‘free commutative monoid’ functor

$S : C \to CommMon (C)$

which is left adjoint to the forgetful functor

$U : CommMon (C) \to C$

There’s a lot more one can say about all this, especially if we keep increasing the number of hypotheses on our category $C$ . But, I’ll stop here and check to see if this is at all relevant to your interests.

By the way, the ‘free commutative monoid’ functor

$S X = 1 + X + X^{\otimes 2} / 2! + \dots$

really deserves to be called $e^{X}$ , for obvious reasons. It’s a categorification of the exponential function. And, in the case when $C = Hilb$ , a very similar functor (but not quite the same, for annoying technical reasons) is called taking the ‘Fock space’ of $X$ . So, taking the Fock space of a Hilbert space is like exponentiation!

I was taught this by Irving Segal, who had no interest whatsoever in category theory.

I later went crazy iterating this Fock space construction in my webpage on nth Quantization. If we start with the 0-dimensional Hilbert space, and take its Fock space, and the Fock space of that, and so on, we get some very interesting and famous things.

This webpage ends with a puzzle that nobody has ever solved to my satisfaction: what’s a nice description of the Fock space of the Fock space of the Fock space of the Fock space of the 0-dimensional Hilbert space?

But, I digress… you haven’t seen anyone iterating BV quantization, have you?

Speaking of iterating, here’s an easier puzzle: what’s $CommMon (CommMon (C))$ like?

Posted by: John Baez on December 1, 2007 6:36 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

We can talk about the free commutative monoid SX on an object X whenever C also has coequalizers and (countable) coproducts:

SX=1+X+X^⊗2/2!+⋯

You just take the symmetrized tensor powers of X and add them up.

when can you get the corresponding symmetric comonoid replacing e.g. X^⊗2/2! by the symmetric invariants?

Posted by: jim stasheff on December 1, 2007 8:24 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Jim wrote:

when can you get the corresponding symmetric comonoid replacing e.g. X^⊗2/2! by the symmetric invariants?

Just remove the prefix “co” wherever it appeared and insert wherever it didn’t!

I formed the free commutative monoid on $X$ by taking the coequalizers of the symmetric group actions on $X^{\otimes n}$ (the symmetric coinvariants) and then taking the coproduct of these for all $n$ .

So, we form the free commutative comonoid on $X$ by taking the equalizers of the symmetric group actions on $X^{\otimes n}$ (the symmetric invariants) and then taking the product of these for all $n$ .

(If some wise guy says I should’ve removed the ‘co’ in ‘commutative’, I’ll slap ‘em.)

The point is that a commmutative comonoid in a symmetric monoidal category $C$ is the same as a commutative monoid in the opposite category, $C^{op}$ .

should it be denoted $1 / (1 - X)$ ?

No, $1 / (1 - X)$ is a good name for the free monoid on an object $X$ , since this is just

$1 + X + X^{2} + \dots$

No symmetric group actions are involved here! We can do this in any monoidal category with (countable) coproducts.

Posted by: John Baez on December 1, 2007 9:03 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

No, $1 / (1 - X)$ is a good name for the free monoid on an object X, since this is just $1 + X + X^{2} + \dots$ No symmetric group actions are involved here! We can do this in any monoidal category with (countable) coproducts.

There’s an important caveat here: the monoidal product $X \otimes Y$ must preserve countable coproducts in each of its separate arguments $X$ and $Y$ in order for this nice construction to work. In practice this is often automatic, especially in cases where the monoidal category is biclosed (which means $X \otimes -$ and $- \otimes Y$ are left adjoints to appropriate Hom-functors – in that case, the left adjoints preserve any colimits which happen to exist, including of course countable coproducts).

But for the same reason, you typically have to be careful in how you construct cofree comonoids in a monoidal category. Even if the monoidal category $C$ has countable products (so that $C^{op}$ has countable coproducts), it is typically not the case that the tensor product will preserve them in separate arguments, which is what is needed in order for the dual of John’s construction to apply.

In rough outline, according to the paper by Getzler and Goerss that I referred to here, the cofree comonoid $Cof (V)$ on a chain complex $V$ of finite type is given by taking the continuous dual of the profinite completion of the tensor algebra (see page 5). For a general chain complex $V$ , they give a proof that $Cof (V)$ is given by the filtered colimit formula

Cof (V) = {colim}_{α} Cof (V_{α})

where the $V_{α}$ range over subcomplexes of finite type. (I’ll assume for now that this is a correct description, although I haven’t checked all the details.)

Posted by: Todd Trimble on December 1, 2007 10:15 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Whoops. And contrary to my original post, I guess you also need the tensor product to distribute over some colimits to get

$S X = 1 + X + X^{\otimes 2} / 2 + \dots$

to be a (commutative) monoid.

Posted by: John Baez on December 2, 2007 12:03 AM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

John wrote:

By the way, the ‘free commutative monoid’ functor $SX = 1 + X + X^{\otimes 2} / 2! + . .$ really deserves to be called $e^{X}$ , for obvious reasons. It’s a categorification of the exponential function. And, in the case when C=Hilb, a very similar functor (but not quite the same, for annoying technical reasons) is called taking the ‘Fock space’ of X. So, taking the Fock space of a Hilbert space is like exponentiation!

I know it’s pretty shameless chiming in to talk about my own work, but it’s a pretty fact that this Fock space endofunctor will in fact translate product to tensor product, for sufficiently well-behaved cases: there are canonical isomorphisms $i_{A, B} : S (A \oplus B) ≃ S (A) \otimes S (B)$ . This just follows from the fact that $S$ is an adjoint functor, constructing the free cocommutative comonoid, so must preserve products — and the tensor product is the categorical product in the category of commutative comonoids.

Anyway, the nice thing is that these Fock spaces will sometimes come with raising and lowering operators, satisfying the commutation relations — and these are canonically defined precisely when the isomorphisms $i_{A, B}$ are unitary!

Posted by: Jamie Vicary on December 1, 2007 9:35 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Okay, I can take a hint

Thanks! Hope I wasn’t too obnoxious.

I’ll stop here and check to see if this is at all relevant to your interests.

Yes, it is!

So let me indicate where I want to go:

above I admitted that I was being somewhat vague when I said that AKSZ form the internal hom in the world of dg-algebras.

It is sold that way, and it is “certainly morally true” (whatever that means). But now I want to get it completely straight. Or as straight as possible at least.

So: I want to understand the (if any) closed structure on

- dg-algebras

- quasi-free dgc-algebras (free graded-commutative algebras with differentials)

- dg-coalgebras

- quasi- free dg-coalgebras

and I want to undertand how the various more or less obvious constructions that one sees appear in the literature, or that one can dream up onself, fit into the general abstract nonsense.

I was busy most of the day with teaching duties. Now I will go to Todd’s detailed description of the closed structure on coDGAs and try to absorb that (thanks Todd! where would I be without the Café??).

A first glance revealed that it might take me a while to unwrap Todd’s description to the degree that I can see whether and how the expectation that I mention at then end of my previosu comment is realized here. All help is appreciated.

But, I digress… you haven’t seen anyone iterating BV quantization, have you?

I have seen BV quantization applied to the 2-particle… and then to the second quantization of the 2-particle!

(Ordinarily called “the string” and “string field theory”.)

In fact, Zwiebach’s BV treatment of bosonic string field theory seems to be one of the two outstanding successes of the BV formalism (next to the Poisson-sigma model quantization and everything related to that.)

But of course that’s not the explicit “iteratation” that you (and I! :-) want to see.

My personal idea is this:

“quantization” of sufficiently nice setups (namely sigma-models of an $n$ -dimensional thing propagating on something and coupled to an $n$ -background bundle) should really be a functor which eats transport functors and spits out quantum propagation functors. But the latter should be “transport functors” again. So we may try to feed them back into the machinery.

BV-formalism is a way to describe how this machine works. So once we really understand it, we’ll iteratre it.

In the comment second quantization to the thread The $n$ -Café Quantum Conjecture I made some comments on this idea of iterating this endofunctor $transport functors \overset{quantization}{\to} transport functors$ and how this does seem to have a good chance to indeed capture the idea of second quantization.

Posted by: urs on December 3, 2007 7:49 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Urs wrote:

P.S. I should add that I am glossing over the following point: I keep talking about the homs in chain complexes. But what we really need here are homs in monoids in chain complexes, namely dg-algebras. This doesn’t change much about the general point here, but I need to eventually discuss this in more detail. And at some point I will actually want to ask the wizards: what is known, from an abstract category-theory point of view, about the category $SymMonoids ({Ch}^{*} (A))$ of symmetric monoids internal to chain complexes ??

As is often the case, I’m not following very well what is really going on in this discussion, so please treat this as a surface-level reaction. It sounds as if you hope there’s an internal $Hom$ , internal to the category of commutative dga’s (commutative monoids in the symmetric monoidal category of chain complexes), i.e., that there’s a closed category structure on the category of commutative dga’s.

That would be too much to hope for, I think, but it reminds me of some facts which I find very interesting:

The category $CoDGA$ of cocommutative comonoids in the category of chain complexes is complete and cocomplete, and the forgetful functor to the category of chain complexes, $U : CoDGA \to Ch,$ admits a right adjoint (cofree cocommutative coalgebra construction). See this ps file by Ezra Getzler and Paul Goerss for details.
The category $CoDGA$ is cartesian closed (the cartesian product is the tensor product in $Ch$ ). I first learned this from Jim Dolan; I can give a proof of this and the following statement on request.
The category of commutative dga’s is enriched in the cartesian closed category $CoDGA$ .

The last part means that if $A$ and $B$ are two commutative dga’s, there is a cocommutative comonoid $Hom (A, B)$ in $Ch$ [which Martin Hyland once told me was called a “measure coalgebra”, if I remember correctly], defined by the following universal property: if $C$ is a cocommutative comonoid in $Ch$ , then the chain complex $hom (C, B)$ carries a commutative dga-structure, and there is a natural isomorphism

DGA (A, hom (C, B)) ≅ CoDGA (C, Hom (A, B)) .

I’m also vaguely wondering whether this can be at all related to what Jim Stasheff was just saying about the need to pass to $A_{∞}$ … I’d have to think further before I can amplify.

Posted by: Todd Trimble on December 1, 2007 6:48 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

I think you answered my last question before I answered it in re: symm comonoid

should it be denoted 1/(1-x)?

but the A_\infty question about maps is
the issue some would hide in the language of derived cats

Posted by: jim stasheff on December 1, 2007 8:27 PM | Permalink | Reply to this

what’s in a name?

Speaking of derived cats, suppose Newton had one and the word fluxion had caught on,
would we now have fluxed cats? financial fluxions might have seemed less esoteric to the casual investor

thoughts provoked by reading Neal Stephenson’s
Con-fusion

Posted by: jim stasheff on December 3, 2007 2:19 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

It sounds as if you hope there’s an internal $Hom$ , internal to the category of commutative dga’s (commutative monoids in the symmetric monoidal category of chain complexes), i.e., that there’s a closed category structure on the category of commutative dga’s.

Yes, that’s the kind of thing I am looking for.

Let’s think rational homotopy theory: DGAs are much like spaces. The morphisms between one space and another should be a space itself.

That would be too much to hope for, I think, but it reminds me of some facts which I find very interesting:

Great, thanks.

The category CoDGA of cocommutative comonoids in the category of chain complexes

I’d be just as happy, or even happier, to discuss CoDGAs instead of DGAs. When everything is suitably finite both should be equivalent (I guess in the ps that you linked to this statement is prop 1.7) and people tend to want to stick with the DGAs as long as possible (or even longer).

But if its just the issue of CoDGAs versus DGAs that prevents me from getting the closed structure that I am looking for, then I won’t hesitate to stick with CoDGAs.

The category CoDGA is cartesian closed

Cool. That’s what I want!

I first learned this from Jim Dolan; I can give a proof of this and the following statement on request.

I’d be very grateful if you indeed did provide the proof. Thanks!

(So this means that this statement is not to be found in the literature??)

I’ll mostly need this statement for CoDGAs which are free as CoGCAs, i.e. for which the underlying graded coalgebra (forgetting the codifferential) is free as a graded commutative coalgebra. But the more general the statement you can provide, the better.

For this last case, I know the following:

let $\lor^{•} V$ be the free graded commutative coalgebra generated from a graded vector space $V$ . Write $(\lor^{•} V, D)$ for the CoDGA obatined by equiupping this coalgebra with a codifferential (degree $\pm 1$ , depending on your conventions) such that $D^{2} = 0$ .

Then a morphism $(\lor^{•} V, D_{V}) \to (\lor^{•} W, D_{W})$ is supposed to be a linear map which is both, a morphism of graded commutative coalgebras and a chain map.

The fact that it is a morphism of free CoGCAs implies that it is entirely fixed by its value on “cogenerators”, hence by maps $f : \lor^{•} V \to W$ (when beginning to think about this it helps to consider the same statement after dualizing everything, where it is more familiar).

Now, for the external hom these maps would be required to respect the differentials $[D, f] = d_{W} f - d_{V} F = 0$ . But for the internal hom we don’t put any restriction on $f$ and instead have the commutator with the codifferentials act as a new codifferential.

This way we should get a new CoDGA $({hom}_{Vect} (\lor^{•}, W), [D, -])$

and I am thinking that this, or something closely related, should be the internal hom.

But there must be some things missing here. Not sure if the above will in general be free, for instance.

Anyway, this is roughly my present understanding. Now I would like to understand this more deeply. Thanks for whatever help you can offer.

Posted by: urs on December 3, 2007 12:59 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

Urs wrote:
Let’s think rational homotopy theory: DGAs are much like spaces. The morphisms between one space and another should be a space itself.

There are more things in the world of rational dgca’s than are dreamt of in
spaces.

Schlessinger and I address this in
“The Lie Algebra Structure of Tangent Cohomology and Deformation Theory,”

Journal of Pure and Applied Algebra 38 (1985) 313-322. (with Michael Schlessinger)
and
in the expanded but never finished `cahier secret’ version
available on demand

Hom(A,B) is fine as a dgca but does not represnet a space in general becasue of those pesky maps of negative degree
so we get the appropriate space by truncating, but not jsut getting rid of the negative stuff - degree 0 gets handled in an ad hoc manner to get a space

Posted by: jim stasheff on December 3, 2007 3:16 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

Jim Stasheff wrote:

Hom(A,B) is fine as a dgca

When you say this, precisely what product structure $Hom (A, B) \otimes Hom (A, B) \to Hom (A, B)$ are you referring to?

but does not represnet a space in general becasue of those pesky maps of negative degree

Okay, thanks. So maybe it represents, in general, instead a spectrum??

so we get the appropriate space by truncating, but not jsut getting rid of the negative stuff - degree 0 gets handled in an ad hoc manner to get a space

I have the papers you mentioned here, may need to look at them more closely, though.

Posted by: urs on December 3, 2007 8:33 PM | Permalink | Reply to this

Re: On BV Quantization, Part VIII

$MathML-enabled post (click for more details).$

I’d be very grateful if you indeed did provide the proof [of the fact that $CoDGA$ is cartesian closed]. Thanks!

Okay, here goes. This proof is supposed to be very “soft” and general. But, you may need to grab pencil and paper to do some side calculations in order to follow this. (We might also humbly beseech the Grand Wizard to sprinkle a little magic sugar over this to make it go down easier, but he may be busy on other errands of mercy.)

By the way, in response to

(So this means that this statement is not to be found in the literature??)

I don’t know. But maybe Jim Dolan knows. I have a feeling this result may have been known to Tom Fox (a categorist at McGill) back in the 80’s, when he was publishing stuff on cocommutative comonoid theory.

First, for any symmetric monoidal category $C$ , the category $Coc$ of cocommutative comonoids has cartesian products given by the monoidal product in $C$ . That is, if $X$ and $Y$ are cocommutative comonoids, then their categorical product is $X \otimes Y$ with the evident structure of cocommutative comonoid. The projections $X \otimes Y \to X$ , $X \otimes Y \to Y$ are formed with the help of the counit $X \to I$ , $Y \to I$ , and the comultiplication $X \to X \otimes X$ plays the role of diagonal map. This is all well known.

Thus, to prove cartesian closure, we must construct, given two cocommutative comonoids $Y$ and $Z$ , a cocommutative comonoid $Hom (Y, Z)$ together with an isomorphism

Coc (X \otimes Y, Z) ≅ Coc (X, Hom (Y, Z))

natural in $X$ . (Then, by the usual yoga of representable functors, there is a canonical way of making $Hom (Y, Z)$ functorial in its arguments $Y$ and $Z$ in such a way that the naturality extends to $Y$ and $Z$ as well.)

Now suppose that $C$ is symmetric monoidal closed. The extra key assumptions we need to prove $Coc$ cartesian closed is that it has equalizers and that the underlying functor

U : Coc \to C

has a right adjoint $Cof$ (the cofree cocommutative comonoid functor). Happily, these assumptions are satisfied in the case of present interest ( $C$ = chain complexes), and for many other symmetric monoidal closed abelian categories, I believe.

Start with a map $f : X \otimes Y \to Z$ in $Coc$ . This means we have two commutative diagrams in $C$ :

\begin{matrix} X \otimes Y & \overset{δ_{X \otimes Y}}{\to} & X \otimes Y \otimes X \otimes Y \\ f ↓ & ↓ f \otimes f \\ Z & \overset{δ_{Z}}{\to} & Z \otimes Z \end{matrix}

and

\begin{matrix} X \otimes Y & \overset{ε_{X} \otimes ε_{Y}}{\to} & I \\ f ↓ & ↗ ε_{Z} \\ Z \end{matrix}

where the comultiplication $δ_{X \otimes Y}$ in the first diagram is the composite

X \otimes Y \overset{δ_{X} \otimes δ_{Y}}{\to} X \otimes X \otimes Y \otimes Y \overset{1 \otimes σ \otimes 1}{\to} X \otimes Y \otimes X \otimes Y .

Let $Z^{Y}$ denote the internal hom in $C$ , and let $\hat{f} : X \to Z^{Y}$ denote the transform of $f : X \otimes Y \to Z$ under the symmetric monoidal closed structure on $C$ . A little calculation shows that the square above transforms into a square in $C$ :

\begin{matrix} X & \overset{δ_{X}}{\to} & X \otimes X \\ \hat{f} ↓ & ↓ ϕ \\ Z^{Y} & \overset{δ_{Z}^{Y}}{\to} & (Z \otimes Z)^{Y} \end{matrix}

where $ϕ$ is the composite

X \otimes X \overset{\hat{f} \otimes \hat{f}}{\to} Z^{Y} \otimes Z^{Y} \overset{\otimes_{1}}{\to} (Z \otimes Z)^{Y \otimes Y} \overset{(Z \otimes Z)^{δ_{Y}}}{\to} (Z \otimes Z)^{Y}

in which $\otimes_{1}$ is a canonical map which expresses the enriched functoriality of the monoidal product.

Let $\tilde{f} : X \to Cof (Z^{Y})$ be the unique map in $Coc$ which lifts the arrow $\hat{f} : X \to Z^{Y}$ through the counit $π : Cof (Z^{Y}) \to Z^{Y}$ of the adjunction $U ⊣ Cof$ . The trick is to see that commutativity of the square above translates into saying that this $\tilde{f}$ equalizes a certain pair of arrows $(Φ, Ψ)$ in $Coc$ of the form

Cof (Z^{Y}) \vec{\to} Cof ((Z \otimes Z)^{Y}) .

Similarly (and I’ll leave this part to you), commutativity of the triangle above translates into saying that $\tilde{f}$ equalizes a certain pair of arrows in $Coc$ of the form

Cof (Z^{Y}) \vec{\to} Cof (I^{Y}) .

Thus, the exponential $Hom (Y, Z)$ in $Coc$ we are after is ultimately expressed as an equalizer in $Coc$ of a certain pair of comonoid maps of the form

Cof (Z^{Y}) \vec{\to} Cof ((Z \otimes Z)^{Y}) \otimes Cof (I^{Y})

(where we are using the fact that the right side is a cartesian product in $Coc$ ).

The construction of $Φ$ and $Ψ$ is a bunch of abstract nonsense. The map

Φ : Cof (Z^{Y}) \to Cof ((Z \otimes Z)^{Y})

is the unique comonoid map which lifts the long horizontal composite $Cof (Z^{Y}) \to (Z \otimes Z)^{Y}$ you see at the bottom of

\begin{matrix} X & \overset{δ_{X}}{\to} & X^{\otimes 2} \\ \tilde{f} ↓ & ↓ \tilde{f} \otimes \tilde{f} \\ Cof (Z^{Y}) & \overset{δ}{\to} & Cof (Z^{Y})^{\otimes 2} & \overset{π \otimes π}{\to} & (Z^{Y})^{\otimes 2} & \overset{\otimes_{1}}{\to} & (Z \otimes Z)^{Y \otimes Y} & \overset{(Z \otimes Z)^{δ_{Y}}}{\to} & (Z \otimes Z)^{Y} \end{matrix}

If you look at it carefully, you should be able to see that the composite arrow from $X^{\otimes 2}$ to $(Z \otimes Z)^{Y}$ in this last diagram is the map $ϕ$ we had above in the square. It follows that

Φ \circ \tilde{f} : X \to Cof ((Z \otimes Z)^{Y})

is the unique comonoid map which lifts one of the legs of that square, namely

X \overset{δ_{X}}{\to} X \otimes X \overset{ϕ}{\to} (Z \otimes Z)^{Y},

through the counit $π : Cof ((Z \otimes Z)^{Y}) \to (Z \otimes Z)^{Y}$ of the adjunction $U ⊣ Cof$ .

Similarly, using the $π$ -naturality square

\begin{matrix} Cof (Z^{Y}) & \overset{π}{\to} & Z^{Y} \\ Cof (δ_{Z}^{Y}) ↓ & ↓ δ_{Z}^{Y} \\ Cof ((Z \otimes Z)^{Y}) & \overset{π}{\to} & (Z \otimes Z)^{Y}, \end{matrix}

it is easy to check, if we put $Ψ = Cof (δ_{Z}^{Y})$ , that $Ψ \circ \tilde{f} : X \to Cof ((Z \otimes Z)^{Y})$ is the unique comonoid map which lifts the other leg of that square,

X \overset{\hat{f}}{\to} Z^{Y} \overset{δ_{Z}^{Y}}{\to} (Z \otimes Z)^{Y} .

If you’ve followed me thus far, then hopefully it will be clear that $\tilde{f}$ equalizes $Φ$ and $Ψ$ iff that square above (translating the fact that $f : X \otimes Y \to Z$ preserves comultiplication) commutes. Thus, modulo the additional exercise which I left to you of carrying out a similar construction which translates preservation of the counit, we are finally done (!).

Posted by: Todd Trimble on December 3, 2007 6:51 PM | Permalink |

The n-Category Café

Skip to the Main Content

November 29, 2007