a nice workout in homological algebra, categories and operads.
Great cosmic coincidence! Let’s talk about this stuff.
Some more or less random questions and/or remarks, all spiraling in more or less on what you have been talking about in this TWF:
So let be our abelian category.
The Dold-Kan correspondence says that we have an equivalence of categories
between simplicial objects in and non-negatively graded chain complexes in . The direction
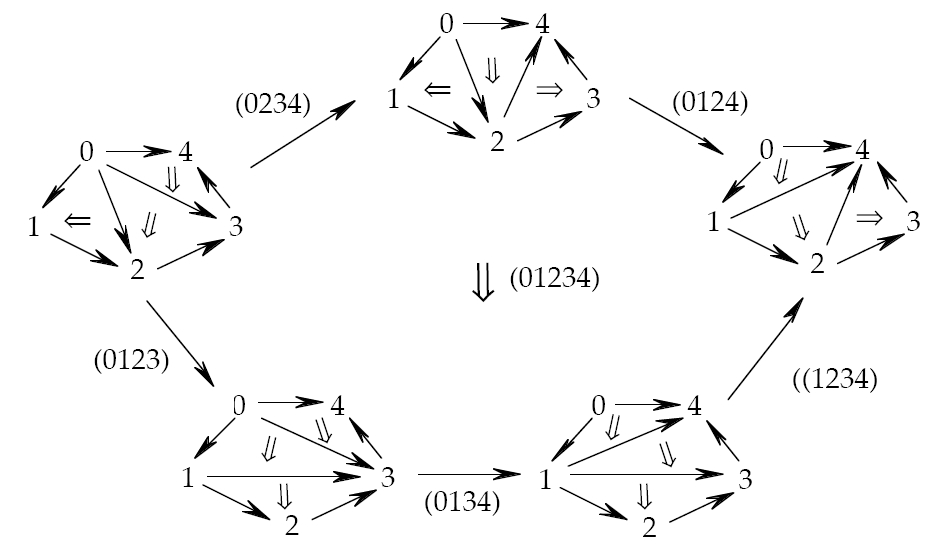
is forming the “normalized chain complex” which corresponds to throwing away lots of face maps except for one at each level, restricting that to the kernel of some of the others, and regarding it as the differential in our complex.
Now, first question: how precisely do I connect this to higher categories now?
I want to combine this with the nerve functor
which sends an -category internal to to its simplicial nerve. I want to get an equivalence
this way. Do I? If not, can you fix this?
This was the first question. Now comes the first big mystery™:
-categories correspond to non-negatively graded chain complexes (and nicely so: in degree of the chain complex we have the space of -morphisms starting at the 0 -morphism, roughly).
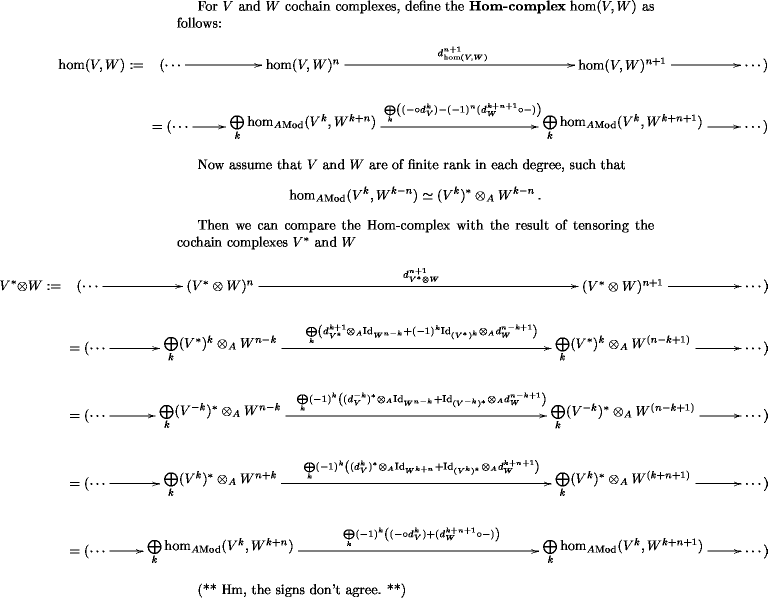
These naturally sit in arbitrarily graded chain complexes. In particular, a couple of nice and natural operations on non-negatively graded chain complexes will produce not-necessarily-non-negatively graded chain complexes from them.
Most notably: forming the dual chain complex and forming the internal hom from that.
So: in the context that -categories correspond to non-negatively graded chain complexes, what corresponds to positively graded chain complexes?
Maybe -co-categories??
Is there a general way in which the “dual” of a category would be a co-category? (Probably like the “dual” of a group, namely functions on the group elements, has a co-algebra structure on it.) (And if so, preferably with everywhere.)
I have Weibel’s book sitting here (Danny’s copy, to be honest) and need to refresh my memory about a bunch of things. It’s been a while.
I’d be most pleased if somebody could give an exegesis of the standard homological algebra constructions entirely in terms of , as far as possible. I sense in John’s TWF the tendency to do just that.
It seems to me that I’d need such an interpretation in order to understand what some easy and obvious constructions in homological algebra mean.
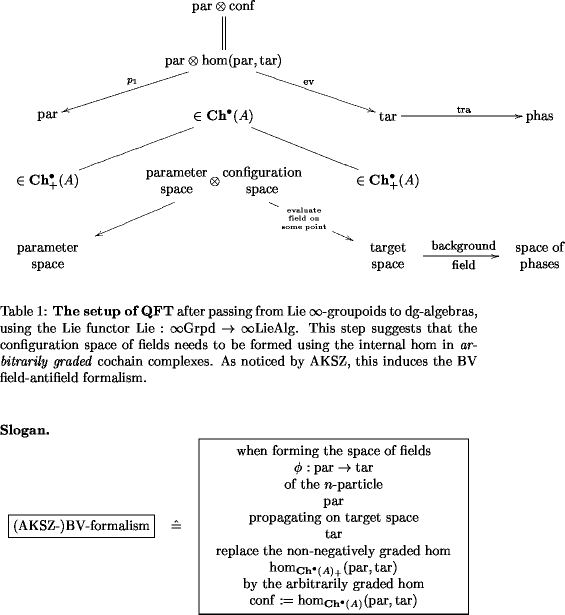
For instance, looking at thet AKSZ paper one finds: they say we should look at two non-negatively graded cochain complexes (parameter space and target space ), but then form the space of fields (the hom object between these two) in the context of arbitrarily graded complexes, hence allowing the complex
to be positively and negatively graded.
(positive = ghosts, negative = anti-xyz).
It’s a simple construction in the homological algebra context. But its true interpretation is quite mysterious (currently to me): both and I know come from certain higher categories. But with negative degrees allowed does not – at least not in the same obvious manner.
So what’s going on??





Re: This Week’s Finds in Mathematical Physics (Week 258)
Great cosmic coincidence! Let’s talk about this stuff.
Some more or less random questions and/or remarks, all spiraling in more or less on what you have been talking about in this TWF:
So let be our abelian category.
The Dold-Kan correspondence says that we have an equivalence of categories between simplicial objects in and non-negatively graded chain complexes in . The direction is forming the “normalized chain complex” which corresponds to throwing away lots of face maps except for one at each level, restricting that to the kernel of some of the others, and regarding it as the differential in our complex.
Now, first question: how precisely do I connect this to higher categories now?
I want to combine this with the nerve functor which sends an -category internal to to its simplicial nerve. I want to get an equivalence this way. Do I? If not, can you fix this?
This was the first question. Now comes the first big mystery™:
-categories correspond to non-negatively graded chain complexes (and nicely so: in degree of the chain complex we have the space of -morphisms starting at the 0 -morphism, roughly).
These naturally sit in arbitrarily graded chain complexes. In particular, a couple of nice and natural operations on non-negatively graded chain complexes will produce not-necessarily-non-negatively graded chain complexes from them.
Most notably: forming the dual chain complex and forming the internal hom from that.
So: in the context that -categories correspond to non-negatively graded chain complexes, what corresponds to positively graded chain complexes?
Maybe -co-categories??
Is there a general way in which the “dual” of a category would be a co-category? (Probably like the “dual” of a group, namely functions on the group elements, has a co-algebra structure on it.) (And if so, preferably with everywhere.)
I have Weibel’s book sitting here (Danny’s copy, to be honest) and need to refresh my memory about a bunch of things. It’s been a while.
I’d be most pleased if somebody could give an exegesis of the standard homological algebra constructions entirely in terms of , as far as possible. I sense in John’s TWF the tendency to do just that.
It seems to me that I’d need such an interpretation in order to understand what some easy and obvious constructions in homological algebra mean.
For instance, looking at thet AKSZ paper one finds: they say we should look at two non-negatively graded cochain complexes (parameter space and target space ), but then form the space of fields (the hom object between these two) in the context of arbitrarily graded complexes, hence allowing the complex to be positively and negatively graded.
(positive = ghosts, negative = anti-xyz).
It’s a simple construction in the homological algebra context. But its true interpretation is quite mysterious (currently to me): both and I know come from certain higher categories. But with negative degrees allowed does not – at least not in the same obvious manner.
So what’s going on??