Formal Concept Analysis
Posted by Simon Willerton
Last time I posted about the nucleus of enriched functors. This time I will post about something a bit (!) less abstract — formal concept analysis — something which has applications in data-mining, software engineering and, possibly, catching terrorists. Next time I’ll post about how these two things come together and can give rise to fuzzy concept analysis.
Formal concept analysis is about extracting the relationships and hierarchies available from the common attributes shared by objects. Let’s try to break up this abstract definition with a concrete example.
In the most basic form of formal concept analysis, the input consists of a set of objects (from the German ‘Gegenstände’), a set of attributes (from the German ‘Merkmale’) and a relation (from the German ‘Inzidenzrelation’) between the objects and the attributes expressing which objects have which attributes. This triple is called the formal context and is often expressed as a table. I don’t feel witty enough today to think up a pertinent Café-based example, so instead I will steal a standard example from the formal concept analysis literature. Here is the table.
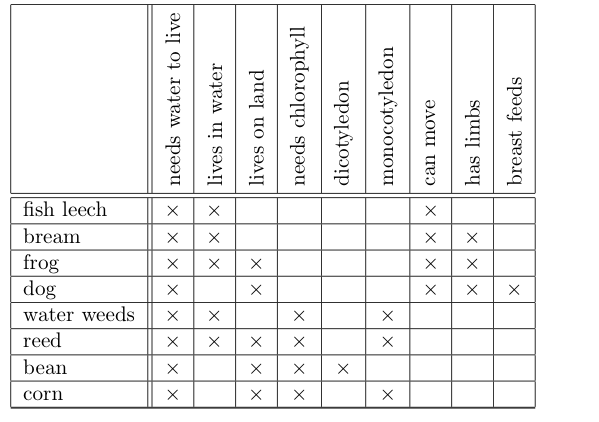
[For non-native English speakers, bream is a kind of fish.]
The output of the analysis is the concept lattice (from the German ‘Begriffsverband’). This is a lattice, which means it is a poset in which each pair of elements have a greatest lower bound and a least upper bound. The concept lattice expresses relationships between the objects and the attributes. Here is the concept lattice for the above example.
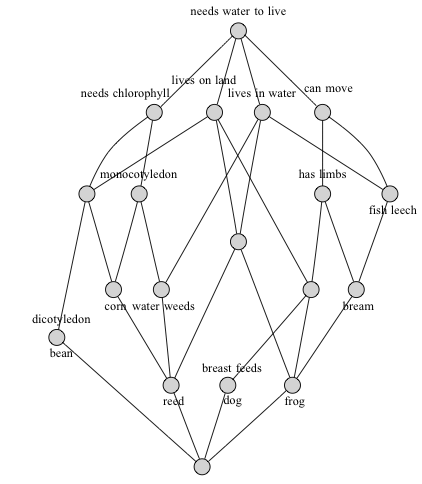
I will explain how you go from the formal context to the concept lattice in the main body below. The relation with my last post is contained in the following slogan.
The concept lattice is the nucleus of the relation .
This comes about by thinking about everything here as being done in the realm of categories enriched over truth values. I’ll explain that next time, but many of you will be able to see that in what you read here.
Formal concept analysis
I don’t know anything about the philosophical roots of the subject but the mathematics of formal concept analysis was fomented in a seminal paper of Rudolf Wille in the 80s.
Wille, Rudolf, “Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts” Ordered Sets. Springer, 1982. 445-470.
The theory was based on Garrett Birkoff’s work on lattice theory of the 30s and developed with Wille’s colleague’s Peter Burmeister and Bernard Ganter in Darmstadt.
I got to meet Bernard Ganter briefly recently by a strange coincidence. Nora Ganter was visiting Sheffield last month from Melbourne. I was talking to her about categorical traces and categorical representations. Over coffee it came out that her father was a mathematician and I realised that it was the Bernard Ganter whose name I had first come across the week before when chasing up some references for my Isbell completion paper. However, not only was he her father, but he was also in Sheffield in the role as baby-sitting grandfather to Nora’s daughter. We managed to have a quick chat before I disappeared off on holiday.
Objects and attributes
Anyway, getting back to the mathematical story, we start with a set of objects and a set of attributes , in our example these are Given a set of objects we can form a set of attributes which is the set of attributes shared by all objects in : So for instance
This gives us a function – the shared attributes function – between power sets . Power sets come with a natural partial order on them, namely that of being a subset. With respect to this, the shared attributes function is order reversing: In words, if you increase the set of objects then you will decrease the set of attributes that they share.
This means we can think of the shared attributes function as an order-preserving function
Similarly we have an order preserving function going the other way which is the objects-with-those-attributes function. So for instance
Galois connections and closure operations
The functions and form what is known as a Galois connection. This means that for all subsets of objects and sets of attributes we have This is clear, because both expressions are just saying that all the objects in have all the attributes in .
A Galois connection gives rise to two closure operations. The closure operations here are and . The closure operation on sets of objects is to take all objects which share all the attributes that the objects in the original set share. So
Similarly, the closure operation for attributes takes a set of attributes and adds in all other attributes which are shared by the objects with the original attributes. So for example It should be reasonably clear that these deserve the name closure operations as they are idempotent, so doing the operation twice doesn’t add anything new.
A closed set of objects is one which is equal to its closure, i.e. such that . So is not closed, but is. A closed set of objects is a maximal set of objects which share some attributes. There is the analogous notion for attributes, so is not closed but is.
The concept of a concept
We now reach the fundamental notion of a concept. A concept consists of a set of objects and a set of attributes such that and . It is immediate that both and are closed. In our example we would have the concept we might call this concept ‘limbed animals’. For a concept the set of objects is called the extent of the concept and the set of attributes is called the intent of the concept.
You can imagine rather bigger examples than our baby example here, such as being the set of all species of animal on the planet and being some suitable set of attributes. I would expect (subject to picking a good set of attributes) that there would be a concept of ‘bird’, with the extent of the concept of bird being the set of all bird species and the intent including attributes such as ‘lays eggs’, ‘has feathers’ and ‘has wings’, but not including ‘can fly’ as we know of bird species such as penguins which can’t fly.
It’s not hard to see that the set of concepts is in bijective correspondence with the set of closed sets of objects. In one direction you just take the extent of the concept, , and in the other direction you take the closed set with its shared attributes, . Similarly we have a bijection with the set of closed sets of attributes. So as sets we have bijections
The ordering on concepts
The set of all concepts has a natural partial order on it given by the notion of a subconcept. For instance, ‘limbed, water-dwelling animal’ is a subconcept of ‘limbed animal’, and it consists of the following Clearly, a subconcept has a reduced extent (set of objects) and an increased intent (set of attributes). Formally, for concepts write if , or equivalently if . This gives the set of concepts the structure of a poset.
You can look back to the top to see a picture of the poset structure on our example.
In fact, the set of concepts is a lattice meaning that each pair of concepts has a greatest lower bound and a least upper bound. Given two concepts and we want to find the least upper bound (or supremum). We know that any upper bound must be a superconcept of both and , so the extent must contain , and the closure is the smallest closed set containing the union so must be the extent of the least upper bound thus However, is the set of attributes shared by everything in the union, and this is the intersection of the set of attributes shared by the objects in and those shared by the objects in . In other words
Similarly, the greatest lower bound, or infimum, is given by taking the closure of the union of the intents.
What has this to do with the nucleus of a profunctor?
Several of you will have realised that the relation can be viewed as a profunctor enriched in truth values, that the Galois connection is an adjunction between presheaf-type enriched categories and the concept lattice is the centre of the adjunction, i.e. the nucleus of the profunctor. I’ll explain this in more detail next time and go on to say how this point of view can be used to generalize to fuzzy concept analysis.

Re: Formal Concept Analysis
Glad to see that a host here get interested in the area that I have been working on during most of my postgraduate period.
Yeah, FCA has a natural closed relationship with profunctors between quantale-enriched categories (or more generally, quantaloid-enriched categories — for FCA on fuzzy sets).
The main theory of FCA can be translated into purely categorical languages. Indeed, the Galois connection of FCA generalizes the Isbell adjunction in category theory. It is also interesting that the Galois connection in another theory in computer science, rough set theory (RST), generalizes Kan extensions in category theory. We refer to them as Isbell adjunctions and Kan adjunctions in a recent paper.