The n-Category Café

Generalized metric spaces

Recall that there is a notion due to Lawvere of a generalized metric space. The essential difference from the notion of classical metric spaces is that for a generalized metric space we don’t impose symmetry, so that in general $d(x,y)\ne d(y,x)$; however, we do impose the triangle inequality and zero self-distance $d(x,x)=0$. A generalized metric space is actually defined to be a category enriched over the extended non-negative real numbers $[0,\infty]$, and this idea creates a bridge between enriched category theory and metric space theory.

Tight span

For classical metric spaces the idea of tight span has cropped up in many places independently over the years and has many applications, it was first discovered by Isbell in 1964. For a classical metric space $M$ the tight span $T(M)$ can be thought of as a minimal contractible classical metric space in which $M$ embeds isometrically.

For generic three- and four-point metric spaces here are pictures of the tight spans.

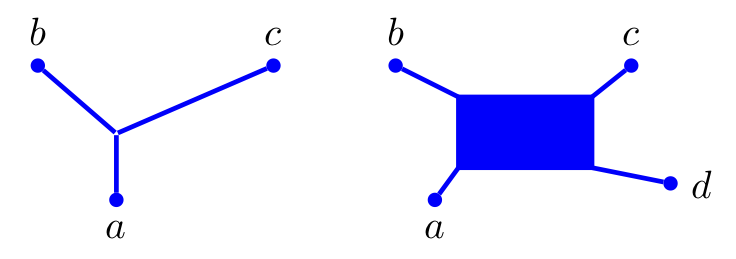
One reason that the tight span is of interest is that $M$ embeds in a tree if and only if the tight span $T(M)$ is a tree, this underlies some of the applications to phylogenetic analysis, i.e. recreating evolutionary trees of species from genetic data. There are also applications to multicommodity flows on networks, server positioning and group cohomology.

Isbell completion

The Isbell completion $I(X)$ for an generalized metric space $X$ is a certain generalized metric space in which $X$ embeds isometrically. There are appropriate notions of categorical completeness and cocompleteness of a metric space (see below for ways of thinking of these) which are not to be confused with the usual notion of metric space completeness. The Isbell completion is complete and cocomplete, moreover the embedding $X\to I(X)$ is continuous and cocontinuous.

The Isbell completion is defined is defined in terms of “presheaves” and “copresheaves” on the space $X$. Presheaves and copresheaves are certain kinds of functions $X\to [0,\infty]$, for example, for a fixed point $x\in X$ the function $d(-,x)$ is a presheaf and the function $d(x,-)$ is a copresheaf. Each point $p$ in the Isbell completion is a pair $(f,g)$ where $f$ is a presheaf and $g$ is a copresheaf, with the interpretation that for any $x\in X$ you have $f(x)$ is the distance to $p$ from $x$ and $g(x)$ is the distance from $p$ to $x$.

For example, the Isbell completion of a generalized metric space with two points is a rectangle (pictured further down this post), the Isbell completion of a classical metric space with three points can be pictured as the union of four polygons in three-space like so.

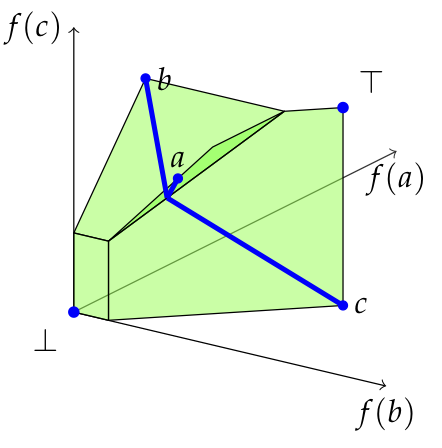
The metric here is an asymmetric version of the $L_\infty$-metric on $\mathbb{R}^3$, so $d((x,y,z),(x',y',z'))\coloneqq max(0, x'-x, y'-y,z'-z)$.

In categorical language, the Isbell completion of a generalized metric space is defined to be the “invariant part” of the “Isbell adjunction” between the space of presheaves and space of op-co-presheaves:

$$L: [0,\infty]^{X^{op}} \leftrightarrow ([0,\infty]^X)^{op}:R$$

with $L(f)(y)\coloneqq \sup_{x\in X}(d(x,y)-f(x))$ and similarly for $R$. So a point is the Isbell completion is a pair $(f,g)$ with $L(f)=g$ and $R(g)=f$.

Tight span and Isbell completion

The connection between the tight span and the Isbell completion is that for a classical metric space $M$ the tight span $T(M)$ is the maximal classical space containing $M$ inside the Isbell completion $I(M)$. For example it is drawn in blue in the above picture of the Isbell completion of a three-point classical metric space. This means that the Isbell completion can be thought of as generalized metric space analogue of the tight span.

Directed tight span

After having figured all of this out I discovered that a couple of Japanese mathematicians, Hirai and Koichi, had defined an analogue of the tight span for what they called “directed metric spaces” which are not quite as general as generalized metric spaces but are the same in that they don’t impose the symmetry of the metric.

H. Hirai and S. Koichi, On tight spans and tropical polytopes for directed distances

They were motivated by applications to multicommodity flow on directed networks. It transpires that their directed tight span is basically the Isbell completion.

Semi-tropical algebra

Tropical mathematics is a broad an active area of mathematics being studied for many reasons, but has at its heart the so-called tropical semi-ring $\mathbf{T}$. (Here the term “semi-ring” means a ring without additive inverses, such a thing is also called a “rig”.) Actually there are a few minor variants of “the” tropical semi-ring but we can take $\mathbf{T}$ to be the extended real numbers $(-\infty,\infty]$ with “min” as the addition – written $\oplus$ – and “usual $+$” as the multiplication – written $\odot$. Then $\infty$ is the additive unit and $0$ is the multiplicative unit. For example,

$$7\oplus 3 =3, \qquad 7\odot 3= 10.$$

The tropical semi-ring is actually a semi-field as all of the non-$\infty$ elements have multiplicative inverses, e.g. $7\odot -7 =0$. We are not interested at this point in the negative reals and will consider the semi-ring $([0,\infty],\oplus, \odot)$. As this is half of the tropical semi-ring I have named it the semi-tropical semi-ring, and we can denote it $\mathbf{S}$.

Modules over the tropical semi-ring are of much interest; a module over a semi-ring is a commutative monoid $(C,\oplus)$ with an action $\odot$, in the usual sense, of the semi-ring on it. As the tropical semi-ring $\mathbf{T}$ is a semi-field, modules over it are free, in particular a module over $\mathbf{T}$ comes with a flow, i.e. an action of the extended reals $(-\infty,\infty]$ on it.

Develin and Sturmfels thought that they were able to show that the classical tight span was a tropical module (modulo the flow), but found an error in their proof. This is the use of the word tropical in Hirai and Koichi’s paper above.

Modules over the semi-tropical semi-ring $\mathbf{S}$ are a bit more mysterious at this point, but in particular they only have a semi-flow, so points can be moved forward in time, if you will, but cannot be moved backwards in time.

Completeness, cocompleteness and semi-tropical modules

We can now go back to completeness and cocompleteness of generalized metric spaces. It transpires that a generalized metric space is cocomplete if and only if it can be given a semi-tropical module structure in a way compatible with the metric. (I should be careful and say that the generalized metric space has to be skeletal there.) Similarly being complete corresponds to being a semi-tropical module in a way differently compatible with the metric. The point here is that generalized metric spaces are enriched over $[0,\infty]$ and it is this that naturally acts.

As the Isbell completion is both complete and cocomplete, it can be given two different semi-tropical modules structures. In the very simple case of an asymmetric generalized metric space with two points, the two semi-tropical module structures $\left(I(X),\oplus, \odot\right)$ and $\left(I(X),\boxplus, \boxdot\right)$ are pictured as follows, where $\tau\in [0,\infty]$.

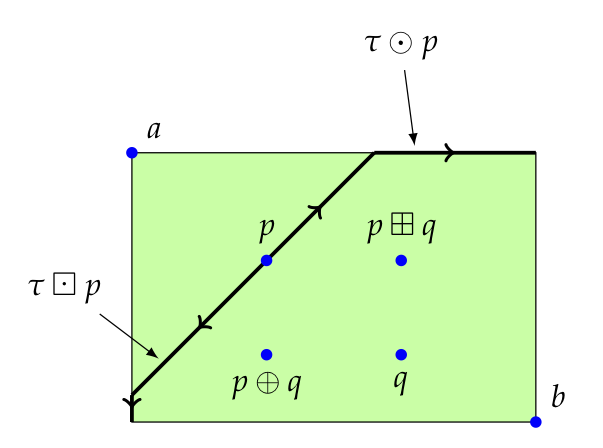
The semi-tropical action on the Isbell completion of three points pictured further up is going to be more complicated.

Anyway, to sum up, from the categorical point of view, gives you various structures that are of interest. In particular, we get these semi-tropical structures naturally occurring on Hirai and Koichi’s tight span which they had not looked at. It seems people were looking for tropical actions.

Postscript: Formal concept analysis

In the last week Dusko Pavlovic pointed me to his paper

D. Pavlovic, Quantitative concept analysis

In this paper he also defines what I’ve termed the Isbell completion for what are essentially generalized metric spaces (but he uses the equivalent context of “proxets”). His motivation and notation are rather different however. He goes on to define a generalization of the Isbell completion for any profunctor $\Phi\colon X\to Y$ between generalized metric spaces, he calls this generalized metric space the “nucleus” of $\Phi$ and it consists of pairs $(f,g)$ where $f$ is a presheaf on $X$ and $g$ is a copresheaf on $Y$. I have some ideas about this, but haven’t thought too much about it yet.