Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

January 26, 2026

Categorifying Riemann’s Functional Equation

Posted by John Baez

David Jaz Myers just sent me some neat comments on this paper of mine:

and he okayed me posting them here. He’s taking the idea of categorifying the Riemann zeta function, explained in my paper, and going further, imagining what it might mean to categorify Riemann’s functional equation

ξ(s)=ξ(1−s) \xi(s) = \xi(1-s)

where ξ\xi is the ‘completed’ Riemann zeta function, which has an extra factor taking into account the ‘real prime’:

ξ(s)=π −s/2Γ(s/2)∏ pprime11−p −s \xi(s) = \pi^{-s/2}\Gamma(s/2) \prod_{p \; prime} \frac{1}{1 - p^{-s}}

My paper categorified the Euler product formula that writes the Riemann zeta function as a product over the usual primes:

ζ(s)=∏ pprime11−p −s \zeta(s) = \prod_{p \; prime} \frac{1}{1 - p^{-s}}

I had nothing to say about the real prime.

But it’s the functional equation that sets the stage for focusing on zeroes of the Riemann zeta function with Re(s)=1/2\text{Re}(s) = 1/2… and then the Riemann Hypothesis! So it’s worth thinking about.

Continue reading “Categorifying Riemann’s Functional Equation” …
Posted at 12:19 AM UTC | Permalink | Post a Comment

January 6, 2026

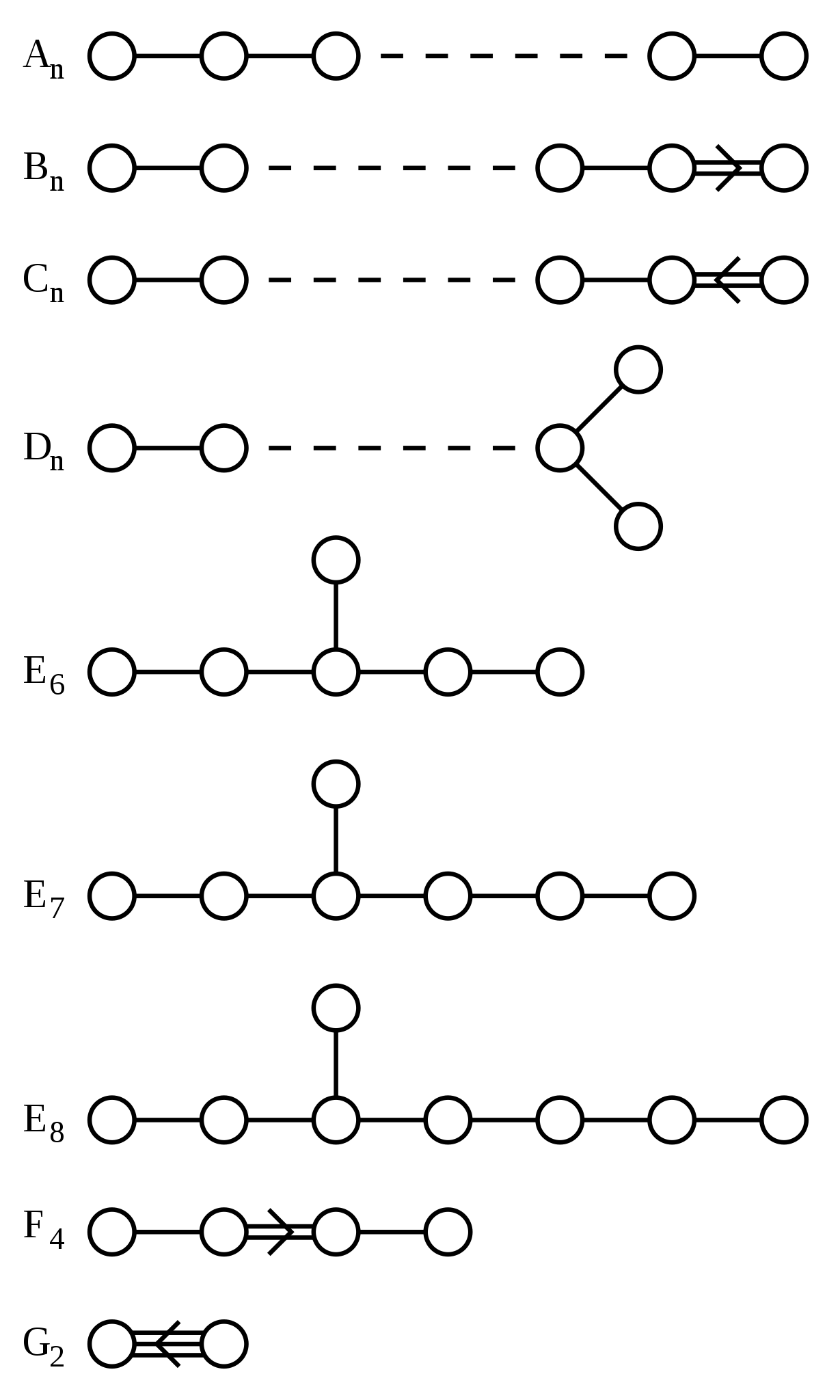
Coxeter and Dynkin Diagrams

Posted by John Baez

Dynkin diagrams have always fascinated me. They are magically potent language — you can do so much with them!

Continue reading “Coxeter and Dynkin Diagrams” …
Posted at 3:44 PM UTC | Permalink | Followups (6)