Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

January 6, 2026

Coxeter and Dynkin Diagrams

Posted by John Baez

Dynkin diagrams have always fascinated me. They are magically potent language — you can do so much with them!

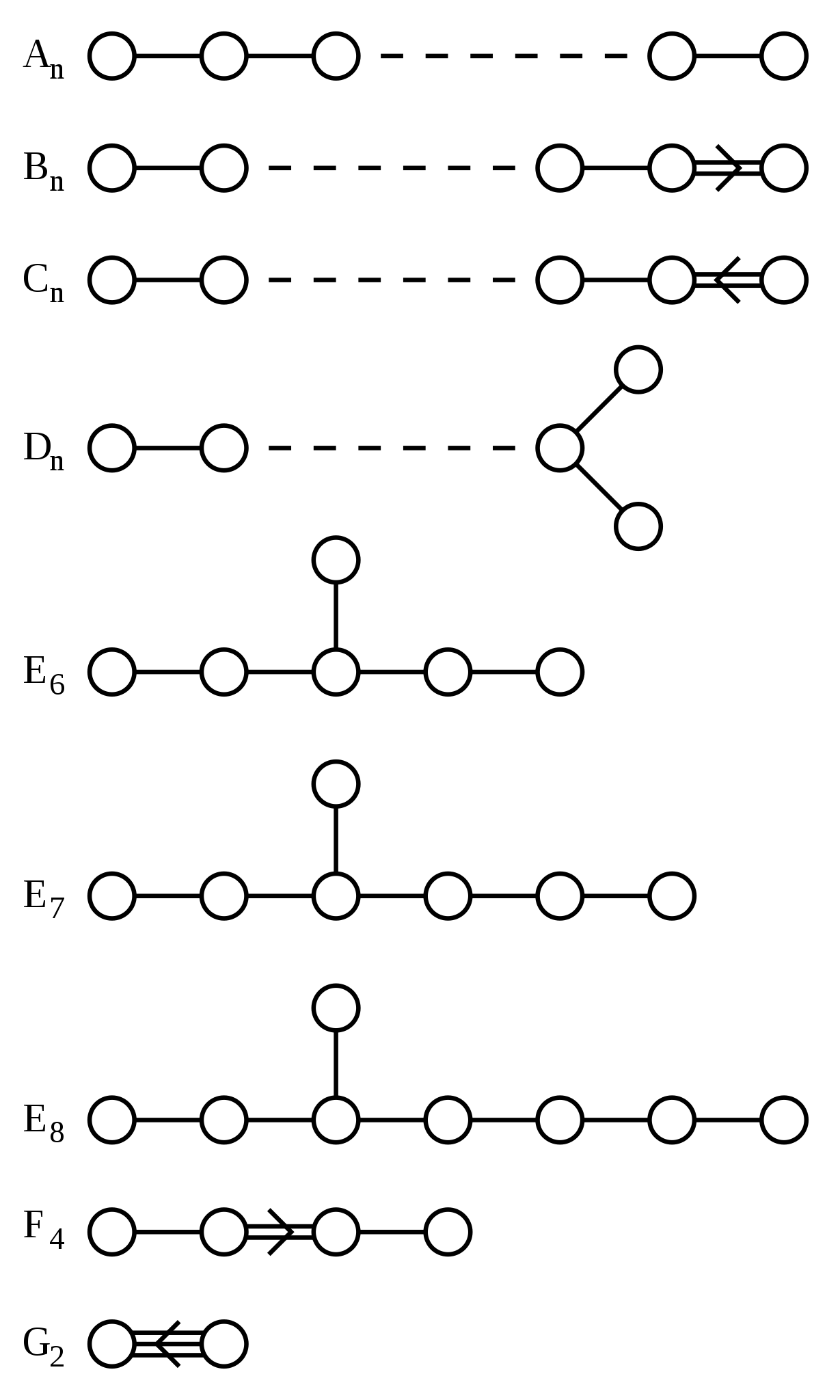
Here’s my gentle and expository intro to Dynkin diagrams and their close relative, Coxeter diagrams:

Abstract. Coxeter and Dynkin diagrams classify a wide variety of structures, most notably finite reflection groups, lattices having such groups as symmetries, compact simple Lie groups and complex simple Lie algebras. The simply laced or “ADE” Dynkin diagrams also classify finite subgroups of SU(2) and quivers with finitely many indecomposable representations. This introductory tour of Coxeter and Dynkin diagrams, based on the column This Week’s Finds in Mathematical Physics, is made to accompany a series of five lecture videos.

I’m a bit sorry that I didn’t probe deeper into why Dynkin diagrams are what they are: that is, why these and no others? I’m also sorry I didn’t dig into the “black magic” that I mention at the end: that is, why does this black magic work? I’d also like to include a little comparison of the 4 lattices you get from the Lie algebra of a compact simple Lie group: the weight lattice, the coweight lattice, the root lattice, and the coroot lattice — merely because I tend to get them confused, and my exposition needed to say a bit about these.

Luckily I can add these other things later. And I think keeping it short and snappy has its own charms.

Posted at January 6, 2026 3:44 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3627



6 Comments & 0 Trackbacks

Re: Coxeter and Dynkin Diagrams

Thank you for all of this and making it available. Some things that I find mysterious about this is what do root systems and the like show up in across mathematics and seem to parameterise many different classifications. They are somehow a fundamental notion but do not feel fundamental. The other thing about them is why do we have these exceptional (or sporadic) ones (you can of course ask that in other classifications like finite simple groups). It has a feeling of weird low(ish); dimensional accidents.

Posted by: Anonymous on January 8, 2026 7:12 AM | Permalink | Reply to this

Re: Coxeter and Dynkin Diagrams

Do you talk about their connection with the Platonic solids and other regular polytopes?

Do you talk about how they relate to groups appearing in physics, such as SO(n), SU(n), and E8?

Posted by: Jeffery Winkler on January 13, 2026 7:22 PM | Permalink | Reply to this

Re: Coxeter and Dynkin Diagrams

Yes.

Yes.

Posted by: John Baez on January 15, 2026 11:56 PM | Permalink | Reply to this

Generating a group with SO(2)s

Here’s something that’s always bugged me about Dynkin diagrams.

On the one hand, you can use the Serre presentation of the (compact, say) Lie group as freely generated by some SU(2)s, modulo relations that say two SU(2)s generate either an SU(2) x SU(2), or an SU(3), or a Spin(5), or G_2. You don’t need relations involving three of the SU(2)s.

On the other, you can use the Coxeter presentation of the Weyl group as freely generated by some Z_2s, modulo similar but easier relations.

I would like to think of these as U(1,H) and U(1,R), automorphisms of 1-dimensional quaternionic or real spaces.

But the easiest version should always be the complex one, surely? – where our group is generated by circle groups U(1,C). And yet nobody seems to talk about this group!

Of course it’ll be a Lie group. One way to get hold of it as a maximal compact inside the split real group (generated by SL(2,R)s instead of SU(2)s). In particular it may not be simple, but so what.

To the extent that I have a question, perhaps it is: what can we understand about a compact Lie group if, instead of following the usual Dynkin recipe that cooks it up from U(1,H)s, we see it as built out of U(1,C)s?

Posted by: Allen Knutson on January 22, 2026 3:36 AM | Permalink | Reply to this

Re: Generating a group with SO(2)s

That’s an interesting puzzle. I don’t have anything great to say about it. It reminds me of how people work with compact reductive groups, where you really need some U(1)’s as well as the usual SU(2)’s. Do people use a different color of dots for these U(1)’s?

Posted by: John Baez on January 22, 2026 5:42 AM | Permalink | Reply to this

Re: Generating a group with SO(2)s

Perhaps a different way of looking at SU(2)SU(2) and ℤ 2\mathbb{Z}_2 is as the automorphism groups of ℍ\mathbb{H} and ℂ\mathbb{C} as algebras over ℝ\mathbb{R}? Which I guess would lead to “what about dots as copies of the trivial group?” and “what about dots as copies of G 2G_2?”

Posted by: Layra on January 23, 2026 12:44 AM | Permalink | Reply to this

Post a New Comment